Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Số chính phương: Định nghĩa, tính chất và các dạng bài tập về số chính phương, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Số chính phương, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Số chính phương: Định nghĩa, tính chất và các dạng bài tập về số chính phương
A. Lý thuyết Số chính phương
1. Định nghĩa Số chính phương
Số chính phương là số bằng bình phương của một số nguyên.
Tức là: Nếu n là số chính phương thì n = k2 (k ∈ Z)
Ví dụ: 4 = 22, 9 = 32, 100 = 102
=> 4, 9, 100 là số chính phương
Số 10 không phải là số chính phương bởi vì căn bậc 2 của 10 bằng 3.16227766017, là một số vô tỷ (thuộc tập I), không phải là số tự nhiên.
Số chính phương còn được gọi là số hình vuông vì số chính phương là bình phương của một số tự nhiên mà diện tích hình vuông là hai cạnh nhân nhau (bình phương của 1 cạnh).
Số chính phương được chia ra làm 2 loại:
- Số chính phương chẵn: một số chính phương được gọi là số chính phương chẵn nếu như nó là bình phương của một số chẵn. Ví dụ: 4, 16, 36... là số chính phương chẵn.
- Số chính phương lẻ: một số chính phương được gọi là số chính phương lẻ nếu như nó là bình phương của một số lẻ. Ví dụ: 9, 49, 81... là số chính phương lẻ.
2.1. Số chính phương chỉ có thể có chữ số tận cùng bằng 0, 1, 4, 5, 6, 9; không bao giờ có chữ số tận cùng bằng 2, 3, 7, 8.
2.2. Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
2.3. Số chính phương chỉ có thể có một trong hai dạng 4n hoặc 4n + 1. Không có số chính phương nào có dạng 4n + 2 hoặc 4n + 3 (n ∈ N).
2.4. Số chính phương chỉ có thể có một trong hai dạng 3n hoặc 3n + 1. Không có số chính phương nào có dạng 3n + 2 (n ∈ N).
2.5. Số chính phương tận cùng bằng 1, 4 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
Số chính phương tận cùng bằng 5 thì chữ số hàng chục là 2.
Số chính phương tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
2.6. Số chính phương chia hết cho 2 thì chia hết cho 4.
Số chính phương chia hết cho 3 thì chia hết cho 9.
Số chính phương chia hết cho 5 thì chia hết cho 25.
Số chính phương chia hết cho 8 thì chia hết cho 16.
2.7. Mọi số chính phương khi chia cho 5, cho 8 chỉ dư 1, 0, 4
Số chính phương chia cho 4 hoặc 3 không bao giờ có số dư là 2
Số chính phương lẻ khi chia 8 luôn dư 1.
2.8. Giữa hai số chính phương liên tiếp không có số chính phương nào.
2.9. Nếu hai số nguyên liên tiếp có tích là một số chính phương thì một trong hai số đó là số 0.
2.10. Số các ước của một số chính phương là số lẻ. Ngược lại, một số có số các ước là số lẻ thì số đó là số chính phương.
2.11. Nếu n2 < k < (n + 1)2 (n ∈ N) thì k không là số chính phương.
2.12. Nếu hai số tự nhiên a và b nguyên tố cùng nhau có tích là một số chính phương thì mỗi số a, b cũng là các số chính phương.
2.13. Số chính phương a chia hết cho số nguyên tố p thì a chia hết cho p2.
2.14. Nếu tích hai số a và b là một số chính phương thì các số a và b có dạng a - mp2; b - mp2.
2.15. Công thức để tính hiệu của hai số chính phương: a2 - b2 = (a + b) . (a - b).
2.16. Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1.
Ví dụ: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 +7, 1 + 3 + 5 +7 + 9, ….
3. Tính chất chia hết của số chính phương
Số chính phương chia hết cho số nguyên tố p thì cũng sẽ chia hết cho p^2, và ngược lại.
- Số chính phương chia hết cho 2 thì chia hết cho 2^2 = 4.
- Số chính phương chia hết cho 3 thì chia hết cho 3^2 = 9.
- Số chính phương chia hết cho 5 thì chia hết cho 5^2 = 25.
- Số chính phương chia hết cho 8 (= 2^3) thì cũng chia hết cho 2^4 = 16 (viết dưới dạng lũy thừa của một số).
- Số chính phương 36 ( 6^2 ) chia hết cho 2 => 36 chia hết cho 4 ( 2^2 )
- Số chính phương 144 ( 12^2 ) chia hết cho 3 (144:3=48) => 144 chia hết cho 9 (144:9=16)
4. Số chính phương nhỏ nhất
Số chính phương nhỏ nhất trong tập hợp các số chính phương sẽ là số 0. Còn trong dãy số từ 0 đến 100 thì có có tất cả 10 số chính phương nhỏ hơn 100. Nó bao gồm số: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81.
5. Số chính phương lớn nhất
- Số chính phương lớn nhất có 1 chữ số là số 9
- Số chính phương lớn nhất có 2 chữ số là số 81
- Số chính phương lớn nhất có 3 chữ số là 312
- Số chính phương lớn nhất có 4 chữ số là 9801
- Số chính phương lớn nhất có 5 chữ số là 99856
6. Hằng đẳng thức để tính hiệu của hai số chính phương
a^2 - b^2 = (a+b)(a-b).
Ví dụ: 6^2 - 3^2 = (6+3)(6-3) = 9.3 = 27.
B. Các dạng bài tập về Số chính phương
Dạng 1. Chứng minh một số là số chính phương
Phương pháp: Để chứng minh một số n là số chính phương ta thường dựa vào định nghĩa, tức là chứng minh n = k2 (k ∊ N).
Bài 1: Chứng minh rằng mọi số nguyên x, y thì:
A = (x + y)(x + 2y)(x + 3y)(x + 4y) + là số chính phương.
Lời giải:
Ta có A = (x + y)(x + 2y)(x + 3y)(x + 4y) + y4
A = [(x + y)(x + 4y)] . [(x + 2y)(x + 3y)] + y4
A = (x2 + 5xy + 4y2)(x2 + 5xy + 6y2) + y4
Đặt x2 + 5xy + 5y2 = t (t ∈ Z), ta có:
A = (t - y2)(t + y2) + y4
A = t2 - y4 + y4
A = t2 = (x2 + 5xy + 5y2)2
Vì x, y, z ∈ Z nên (x2 + 5xy + 5y2) ∈ Z.
Vậy A là số chính phương.
Bài 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Lời giải:
Gọi 4 số tự nhiên liên tiếp đó là: n, n + 1, n + 2, n + 3 (n ∈ Z). Ta có:
B = n(n + 1)(n + 2)(n + 3) + 1
B = [n(n + 3)].[(n + 1)(n + 2)] + 1
B = (n2 + 3n)(n2 + 3n + 2) + 1
Đặt n2 + 3n = t (t ∈ N) ta có:
B = t(t + 2) + 1
B = t2 + 2t + 1
B = (t + 1)2
B = (n2 + 3n + 1)2
Vì n ∈ N nên n2 + 3n + 1 ∈ N. Vậy n(n + 1)(n + 2)(n + 3) + 1 là số chính phương.
Dạng 2: Chứng minh một số không là số chính phương
Phương pháp: Để chứng minh n không là số chính phương, ta có thể sử dụng các cách sau:
Bài 1: Một số tự nhiên có tổng các chữ số bằng 2018 thì có thể là số chính phương được không? Tại sao?
Lời giải:
Gọi số tự nhiên có tổng các chữ số bằng 2018 là n.
Ta có: 2018 = 3m + 2 nên số tự nhiên n chia 3 dư 2, do đó n có dạng 3k + 2 với k là số tự nhiên.
Mặt khác, số chính phương không có dạng 3k + 2
Suy ra số tự nhiên n không là số chính phương.
Bài 2: Cho A = 1 + 2 + 22 + 23 + ... + 233. Hỏi A có là số chính phương không? Vì sao?
Lời giải:
Ta có: A = 1 + 2 + 22 + 23 + ... + 233
A = 3 + 22 . (1 + 2 + 22 + 23) + ... + 230 . (1 + 2 + 22 + 23)
A = 3 + 2 . 30 + ... + 229 . 30
A = 3 + (2 + ... + 229) . 30
Ta thấy A có chữ số tận cùng là 3 nên A không là số chính phương.
Dạng 3: Điều kiện để một số là số chính phương
Phương pháp: Vận dụng các phương pháp sau:
Tìm số nguyên dương n để các biểu thức sau là số chính phương:
a) A = n2 - n + 2
b) B = n5 - n + 2
Lời giải:
a) Với n = 1 thì A = 12 - 1 + 2 = 2 không là số chính phương
Với n = 2 thì A = 22 - 2 + 2 = 4 là số chính phương
Với n > 2 thì A = n2 - n + 2 không là số chính phương vì:
(n - 1)2 = n2 - 2n + 1 < n2 - n - 2 < n2
Vậy n = 2 thì A là số chính phương.
b) Ta có: B = n5 - n + 2 = (n2 - 1) . n . (n2 + 1)
Với n = 5k thì n chia hết cho 5
Với n = 5k ± 1 thì n2 - 1 chia hết cho 5
Với n = 5k ± 2 thì n2 + 1 chia hết cho 5
Do đó n5 - n luôn chia hết cho 5
Nên n5 - n + 2 chia cho 5 dư 2
Suy ra n5 - n + 2 có chữ số tận cùng là 2 hoặc 7 nên B = n5 - n + 2 không là số chính phương.
Vậy không có giá trị nào của n thỏa mãn để B là số chính phương.
Dạng 4: Tìm giá trị của biến để biểu thức là số chính phương
Bài 1: Tìm số tự nhiên n sao cho các số sau là số chính phương:
a) n2 + 2n + 12
b) n(n + 3)
c) 13n + 3
d) n2 + n + 1589
Lời giải:
a) Vì n2 + 2n + 12 là số chính phương nên đặt n2 + 2n + 12 = k2 (k ∊ N)
(n2 + 2n + 1) + 11 = k2
⇔ k2 – (n + 1)2 = 11
⇔ (k + n + 1)(k – n - 1) = 11
Nhận xét thấy k + n + 1 > k - n - 1 và chúng là những số nguyên dương, nên ta có thể viết
(k + n + 1) (k - n - 1) = 11 . 1
![]()
b) Đặt n(n + 3) = a2 (n ∊ N)
⇒ n2 + 3n = a2
⇔ 4n2 + 12n = 4a2
⇔ (4n2 + 12n + 9) – 9 = 4a2
⇔ (2n + 3)2 – 4a2 = 9
⇔ (2n + 3 + 2a).(2n + 3 – 2a) = 9
Nhận xét thấy 2n + 3 + 2a > 2n + 3 – 2a và chúng là những số nguyên dương, nên ta có thể viết (2n + 3 + 2a)(2n + 3 – 2a) = 9 . 1
![]()
c) Đặt 13n + 3 = y2 (y ∊ N)
⇒ 13(n - 1) = y2 – 16
⇔ 13(n - 1) = (y + 4)(y – 4)
⇒ (y + 4)(y – 4) chia hết cho 13
Mà 13 là số nguyên tố nên y + 4 chia hết cho 13 hoặc y – 4 chia hết cho 13
⇒ y = 13k ± 4 (với k ∊ N)
⇒ 13(n - 1) = (13k ± 4)2 – 16 = 13k . (13k ± 8) = 13k2 ± 8k + 1
Vậy n = 13k2 ± 8k + 1 (với k ∊ N) thì 13n + 3 là số chính phương
d) Đặt n2 + n + 1589 = m2 (m ∊ N)
⇒ (4n2 + 1)2 + 6355 = 4m2
⇔ (2m + 2n + 1) (2m – 2n – 1) = 6355
Nhận xét thấy 2m + 2n + 1 > 2m – 2n – 1 > 0 và chúng là những số lẻ
Nên ta có thể viết (2m + 2n + 1) (2m – 2n – 1) = 6355 . 1 = 1271 . 5 = 205 . 31 = 155 . 41
Suy ra n có thể có các giá trị sau: 1588; 316; 43; 28
Dạng 5: Tìm số chính phương
Bài 1: Cho A là số chính phương gồm 4 chữ số. Nếu ta thêm vào mỗi chữ số của A một đơn vị thì ta được số chính phương B. Hãy tìm các số A và B.
Lời giải:
Gọi A = ![]() . Nếu thêm vào mỗi chữ số của A một đơn vị thì ta có số
. Nếu thêm vào mỗi chữ số của A một đơn vị thì ta có số
B = ![]() với k, m ∊ N và 32 < k < m < 100 và a, b, c, d =
với k, m ∊ N và 32 < k < m < 100 và a, b, c, d = ![]()
Ta có:
A = ![]()
B = ![]() . Đúng khi cộng không có nhớ
. Đúng khi cộng không có nhớ
m2 – k2 = 1111 ⇔ (m - k)(m + k) = 1111 (*)
Nhận xét thấy tích (m – k)(m + k) > 0 nên m – k và m + k là 2 số nguyên dương.
Và m – k < m + k < 200 nên (*) có thể viết (m – k) (m + k) = 11 . 101
Do đó:
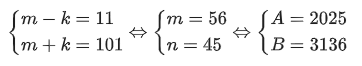
![]()
C. Bài tập Số chính phương
Bài 1: Chứng minh rằng với mọi số nguyên x, y thì
![]() là số chính phương.
là số chính phương.
Ta có
![]()
![]()
Đặt ![]()
![]() thì
thì
![]()
Vì ![]() nên
nên ![]() ⇒
⇒ ![]()
Vậy A là số chính phương.
Bài 2: Chứng minh tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
Gọi 4 số tự nhiên, liên tiêp đó là n, n + 1, n+ 2, n + 3 ![]() . Ta có
. Ta có
![]() =
= ![]()
= ![]() (*)
(*)
Đặt ![]() thì
thì
(*) = ![]() =
= ![]() =
= ![]()
= ![]()
Vì ![]() nên
nên ![]() Vậy
Vậy ![]() là số chính phương.
là số chính phương.
Bài 3: Cho ![]()
Chứng minh rằng ![]() là số chính phương.
là số chính phương.
Ta có
![]()
= ![]()
= ![]()
= ![]()
⇒ ![]()
![]() =
= ![]()
![]()
Theo kết quả bài 2 ⇒ ![]() là số chính phương.
là số chính phương.
Bài 4: Cho dãy số 49; 4489; 444889; 44448889; …
Dãy số trên được xây dựng bằng cách thêm số 48 vào giữa số đứng trước nó. Chứng minh rằng tất cả các số của dãy trên đều là số chính phương.
 Ta có
Ta có
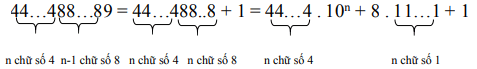
![]()
![]()
![]()
Ta thấy  ữố có tổng các chữ số chia hết cho 3 nên nó chia hết cho 3
ữố có tổng các chữ số chia hết cho 3 nên nó chia hết cho 3
⇒ ![]() hay các số có dạng 44…488…89 là số chính phương.
hay các số có dạng 44…488…89 là số chính phương.
Bài 5: Chứng minh rằng các số sau đây là số chính phương:
 ữốữố
ữốữố
 ữốữốữố
ữốữốữố
 ữốữốữố
ữốữốữố
Kết quả:  ;
;  ;
; 
Bài 6: Chứng minh rằng các số sau là số chính phương:
a) 
b) 
a) ![]()
![]()
![]()
![]()
![]()
⇒ A là số chính phương.
b) 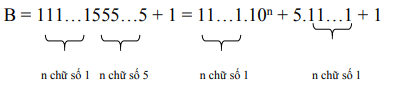
![]()
![]()
 là số chính phương (điều phải chứng minh)
là số chính phương (điều phải chứng minh)
Bài 7: Số chính phương gồm cả 4 chữ số 0 2 3 5 là số nào?
Ta sẽ gọi số cần tìm là abcd.
Vì là số chính phương phải có tận cùng bằng 0 hoặc 5, kết hợp với tính chtaas bất cứ số nào có 0 đứng cuối bình phương nên đều dư 1 số 0, nên ta biểu diễn số cần tìm dưới dạng : abc5.
Ta có 6 cách thay thế 0, 2, 3 vào abc: 0235, 0325, 2305, 2035, 3025, 3205.
Vậy số cần tìm là 3025, vì 3025 = 55^2.
Kết luận: Vậy, số chính phương gồm bốn chữ số 0 2 3 5 chính là 3025.
Bài 8: Chứng minh số n = 2004^2 + 2003^2 + 2002^2 – 2001^2 không phải là số chính phương.
Ta thấy chữ số tận cùng của các số 2004^2, 2003^2, 2002^2, 2001^2 lần lượt là 6,9,4,1. Do đó số n có chữ số tận cùng là 8 nên n không phải là số chính phương.
Bài 9: Chứng minh 1234567890 không phải là số chính phương.
Ta thấy số 1234567890 chia hết cho 5 vì chữ số tận cùng là 0 nhưng lại không chia hết cho 25 vì hai chữ số tận cùng là 90. Vì vậy, số 1234567890 không phải là số chính phương.
Bài 10: Chứng minh một số là số chính phương Chứng minh: Với mọi số tự nhiên n thì A = n(n+1)(n+2)(n+3) + 1 là số chính phương.
Ta có:
A = n(n+1)(n+2)(n+3) + 1
= n.(n+3).(n+1).(n+2) + 1
= (n² + 3n)(n² + 3n + 2) + 1
Khi đó đặt x = n² + 3n với x € số tự nhiên.
Khi đó: A = x ( x +2) + 1 = x² + 2x + 1 = (x+1)² = (n² + 3n + 1)²
Vì n là số tự nhiên nên n² + 3n + 1 cũng thuộc số tự nhiên.
Vì thế A = n(n+1)(n+2)(n+3) + 1 là một số chính phương.
Bài 11: Cho dãy số sau, số nào là số chính phương 9, 81, 790, 400, 121, 380, 2500, 441, 560.
Trong dãy số trên các số là số chính phương là: 9 = 3²; 81 = 9²; 121 = 11²; 2500 = 25²; 400 = 20²; 441 = 21²
Bài 12: Tìm số tự nhiên x sao cho những số dưới đây là số chính phương: A = x²+ 2x + 12.
A = x²+ 2x + 12
Để A là số chính phương, ta có:
x²+ 2x + 12 = n²
<=> (x²+ 2x + 1) + 11 = n²
<=> n² - (x + 1)² = 11
<=> (n + x + 1) . (n - x - 1) = 11
Nhận thấy (n + x + 1) > (n - x - 1) và đều là các số nguyên dương nên có thể viết như sau:
(n + x + 1) . (n - x - 1) = 11 . 1
Giải hệ phương trình:
n + x + 1 = 11
n - x - 1 = 1
Ta được n = 6, x = 4
Vậy số tự nhiên phải tìm là 4.