Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Hình lăng trụ là gì? Tính chất Hình lăng trụ; Các dạng hình lăng trụ thường gặp, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Hình lăng trụ, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Hình lăng trụ là gì? Tính chất Hình lăng trụ; Các dạng hình lăng trụ thường gặp

A. Lý thuyết Hình lăng trụ

1. Định nghĩa

Hình gồm hai đa giác A₁A₂...A_n, A₁’A₂’...A_n’ và các hình bình hành A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, ..., A_nA₁A₁’A_n’ được gọi là hình lăng trụ, kí hiệu là A₁A₂...A_n.A₁’A₂’...A_n’.

Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,... thì hình lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác (Hình 19),...

Trong hình lăng trụ A₁A₂...A_n.A₁’A₂’...A_n’:

– Hai đa giác A₁A₂...A_n và A₁’A₂’...A_n’ gọi là hai mặt đáy;

– Các hình bình hành A₁A₂A₂’A₁’, A₂A₃A₃’A₂’, ..., A_nA₁A₁’A_n’ gọi là các mặt bên;

– Các cạnh của hai mặt đáy gọi là các cạnh đáy;

– Các đoạn thẳng A₁A₁’, A₂A₂’, ..., A_nA_n’ gọi là các cạnh bên;

– Các đỉnh của hai mặt đáy gọi là các đỉnh của hình lăng trụ.

2. Tính chất

Hình lăng trụ có:

⦁ Các cạnh bên song song và bằng nhau.

⦁ Các mặt bên là các hình bình hành.

⦁ Hai mặt đáy là hai đa giác có các cạnh tương ứng song song và bằng nhau.

Ví dụ 1. Cho hình lăng trụ ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm của các tam giác ABC, A’B’C’. Lấy điểm M trên cạnh AC sao cho AM = 2MC. Chứng minh:

a) GM // (BCC’B’).

b) (GG’M) // (BCC’B’).

Hướng dẫn giải

a) Gọi I là trung điểm BC.

Vì G là trọng tâm của tam giác ABC nên $\frac{AG}{AI}=\frac{2}{3}$.

Lại có AM = 2MC, suy ra $\frac{AM}{AC}=\frac{2}{3}$.

Khi đó $\frac{AG}{AI}=\frac{AM}{AC}$.

Áp dụng định lí Thales đảo, ta được GM // BC.

Suy ra GM // (BCC’B’)   (1)

b) Ta có G, G’ lần lượt là trọng tâm của các tam giác ABC, A’B’C’ bằng nhau

Suy ra AG = A’G’ và AG // A’G’.

Do đó tứ giác AGG’A’ là hình bình hành.

Vì vậy AA’ // GG’.

Mà AA’ // BB’ (do ABB’A’ là hình bình hành).

Suy ra GG’ // BB’.

Do đó GG’ // (BCC’B’)    (2)

Trong (GG’M): GM ∩ GG’ = G   (3)

Từ (1), (2), (3), ta thu được (GG’M) // (BCC’B’).

Một số lăng trụ thường gặp

Hình hộp đứng

- Định nghĩa: hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy

- Tính chất: hình hộp đứng có hai đáy là hình bình hành, bốn mặt xung quanh là bốn hình chữ nhật.

Hình hộp chữ nhật

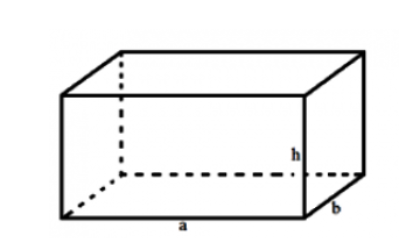
- Định nghĩa: hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

- Tính chất: hình hộp chữ nhật có sáu mặt là sáu hình chữ nhật.

• Hình chữ nhật có 12 cạnh, 8 đỉnh và 6 mặt
• Các đường chéo có hai đầu mút là hai đỉnh đối nhau của hình hộp chữ nhật đồng quy tại một điểm
• Diện tích của hai mặt đối diện trong hình hộp chữ nhật bằng nhau
• Chu vi của hai mặt đối diện trong hình hộp chữ nhật bằng nhau

Hình lập phương

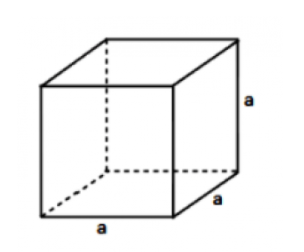
- Định nghĩa: hình lập phương là hình hộp chữ nhật 2 đáy và 4 mặt bên đều là hình vuông

- Tính chất: hình lập phương có 6 mặt đều là hình vuông

• Khối lập phương là hình đa diện đều loại ( 4;3 ). Các mặt là hình vuông, mỗi đỉnh là đỉnh chung của ba mặt
• Khối lập phương có 6 mặt, 8 đỉnh, 12 cạnh

B. Bài tập Hình lăng trụ

Câu hỏi trắc nghiệm

Câu 1: Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại A, AB = AC = a, AA' = 2a. Thể tích khối lăng trụ ABC. A'B'C' là:

A.

B.2a

C.

D.a

Câu 2: Cho lăng trụ đứng tam giác ABC. A'B'C' có đáy là tam giác vuông cân tại A, cạnh AB = , góc giữa A'C với mặt phẳng ABC bằng 45°. Tính thể tích của khối lăng trụ.

A.

B.

C.

D.

Câu 3: Tính thể tích của hình lập phương có độ dài đường chéo bằng 

A. 8

B.24

C.12

D.16

Câu 4: Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối lăng trụ đã cho bằng

A.

B.

C.

D.

Câu 5: Cho khối lăng trụ có diện tích đáy bằng 3a và khoản cách giữa hai đáy bằng a. Tính thể tích V của khối lăng trụ đã cho.

A.

B. 

C. 

D. 

Câu 6: Thể tích khối lập phương có cạnh 2a bằng

A.

B.

C.

D.

Câu 7: Thể tích khối lăng trụ tam giác đều có tất cả các cạnh bằng a là:

A.

B.

C.

D.

Câu 8: Cho hình lăng trụ đứng ABC.A'B'C' có đáy tam giác ABC vuông, AB = BC = a, cạnh bên A'A = . Tính theo a thể tích của khối lăng trụ ABC. A'B'C.

A.

B.

C.

D.

Câu 9: Cho khối lăng trụ đứng ABC.A'B'C' có BB' = a, đáy ABC là tam giác vuông cân tại B và AC = . Tính thể tích V của khối lăng trụ đã cho.

A. 

B.

C.

D.

Câu 10: Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a, A'C hợp với mặt đáy một góc 60°. Thể tích của khối lăng trụ ABC.A'B'C' tính theo bằng:

A.

B.

C.

D.

Câu 11: Thể tích khối hộp chữ nhât ABC.A'B'C'D có các cạnh AB = 3, AD = 4, AA' = 5 là 

A. 

B.

C.

D.

Câu 12: Ông A dự định sử dụng hết 6,5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng ( các mối ghép có dạng kích thước không đáng kể ). Bể cá có dung tích lớn nhất bằng bao nhiêu ( kết quả làm tròn đến hàng trăm )?

A.2.26 m

B.1.61 m

C.1.33 m

D. 1.5 m

Câu 13: Cho llăngtruj ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng ABC trùng với tâm O của đường tròng ngoại tiếp tam giác ABC, biết A'O = a. Tính thể tích khối lăng trụ đã cho.

A.

B.

C.

D.

Câu 14: Cho lăng trụ ABC. A'B'C' có đáy ABC là tam giác cân tại A, AB = AC = a, góc BAC = 120°, hình chiếu vuông góc của A' trên mặt phẳng ABC trùng với trọng tâm tam giác ABC, cạnh bên AA' = a. Thể tích của khối lăng trụ là:

A.

B.

C.

D.

Bài tập tự luyện

Bài 1. Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. Chứng minh:

a) Tứ giác MNC’C là hình bình hành.

b) (B’MC) // (ANC’).

Hướng dẫn giải

a) Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.

Suy ra MN là đường trung bình của hình bình hành ABB’A’.

Do đó MN // BB’ và MN = BB’.

Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).

Suy ra MN // CC’ và MN = CC’.

Vậy tứ giác MNC’C là hình bình hành.

b) Ta có ABB’A’ là hình bình hành.

Suy ra A’B’ // AB và A’B’ = AB.

Mà M, N lần lượt là trung điểm của AB, A’B’.

Do đó B’N // AM và B’N = AM.

Vì vậy tứ giác AMB’N là hình bình hành.

Khi đó AN // B’M.

Suy ra AN // (B’MC)   (1)

Ta có tứ giác MNC’C là hình bình hành, suy ra NC’ // MC.

Do đó NC’ // (B’MC)  (2)

Trong (ANC’) có N = AN ∩ NC’   (3)

Từ (1), (2), (3), ta thu được (ANC’) // (B’MC).

Bài . Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh BB’, CC’.

a) Xác định giao tuyến d của hai mặt phẳng (AMN) và (A’B’C’).

b) Chứng minh d // (ABC).

Hướng dẫn giải

a) Trong (AA’C’C): gọi D = A’C’ ∩ AN.

Mà A’C’ ⊂ (A’B’C’) và AN ⊂ (AMN).

Suy ra D đều thuộc hai mặt phẳng (AMN) và (A’B’C’)   (1)

Trong (AA’B’B): gọi E = AM ∩ A’B’.

Mà AM ⊂ (AMN) và A’B’ ⊂ (A’B’C’).

Suy ra E đều thuộc hai mặt phẳng (AMN) và (A’B’C’)   (2)

Từ (1), (2), suy ra DE là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) hay d ≡ DE.

b) Hình bình hành BCC’B’, có: M, N lần lượt là trung điểm của BB’, CC’.

Suy ra MN là đường trung bình của hình bình hành BCC’B’.

Do đó MN // B’C’ // BC.

Ta có:

⦁ MN = (AMN) ∩ (MNC’B’);

⦁ B’C’ = (A’B’C’) ∩ (MNC’B’);

⦁ DE = (AMN) ∩ (A’B’C’);

⦁ MN // B’C’ (chứng minh trên).

Suy ra DE // MN // B’C’.

Mà B’C’ // BC (chứng minh trên).

Do đó DE // BC.

Mà BC ⊂ (ABC).

Vậy DE // (ABC) hay d // (ABC).