Tailieumoi.vn xin giới thiệu tới bạn đọc tài liệu về Hình lăng trụ đứng: Lý thuyết và các dạng hình lăng trụ đứng, tài liệu gồm đầy đủ về lý thuyết Hình lăng trụ đứng, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Hình lăng trụ đứng: Lý thuyết và các dạng hình lăng trụ đứng
A. Lý thuyết Hình lăng trụ đứng
1. Hình lăng trụ đứng tam giác
- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
- Hai mặt đáy cùng là tam giác và song song với nhau; Mỗi mặt bên là hình chữ nhật;
- Các cạnh bên bằng nhau;
- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
Ví dụ:
Hình lăng trụ đứng tam giác ABC.A'B'C' có:
- Đáy dưới là tam giác ABC, đáy trên là tam giác A'B'C';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CA, A'B', B'C', C'A'
+ Cạnh bên: AA', BB', CC';
- Các đỉnh: A, B, C, A', B', C'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC'.
2. Hình lăng trụ đứng tứ giác
- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Ví dụ:
Hình lăng trụ đứng tứ giác ABCD.A'B'C'D' có:
- Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A'B'C'D';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Các cạnh bên: AA', BB', CC', DD' bằng nhau.
- Các đỉnh: A, B, C, D, A', B', C', D'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC' hoặc DD'.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
Ví dụ:
a) Cho hình lăng trụ đứng tam giác ABC.A'B'C'.
Sxq = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A'B'C'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC').
V = S . h, trong đó S là diện tích tam giác ABC (hoặc A'B'C'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC').
b) Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D':
Sxq = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC', hoặc DD').
V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC', hoặc DD').
B. Bài tập Hình lăng trụ đứng
Bài tập trắc nghiệm
Bài 1: Số cạnh của một đáy của hình dưới đây là :
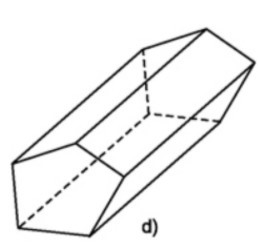
A. 6
B. 3
C. 4
D. 5
Đáp án: D
Ta thấy đáy là một ngũ giác và có số cạnh là 5
Bài 2: Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Các cặp mặt phẳng cho dưới đây cặp nào song song
A. mp(ABB’A’) // mp(BCC’B’)
B. mp(ABC)//mp(ACC’A’)
C. mp(ABC)//mp(A’B’C’)
D. mp(ABB’A’)//mp(ACC’A’)
Đáp án: C
Giải thích:
Hai mặt phẳng song song trong lăng trụ đứng tam giác ABC.A’B’C’ là mp(ABC) và mp(A’B’C’)
Bài 3: Cho hình lăng trụ đứng ABCD. A’B’C’D’ có đáy ABCD là hình thang vuông ( = = 900)
Có bao nhiêu cạnh song song với mặt phẳng (ABB’A’)?
A. 1
B. 2
C. 4
D. 5
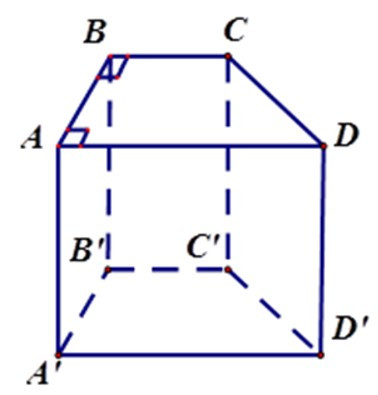
Vì CC’//BB’, DD’//AA’nên các đường thẳn DD’, CC’ song song với mp (ABB’A’)
Bài 4: Hình dưới đây có tổng số cạnh của hai đáy là
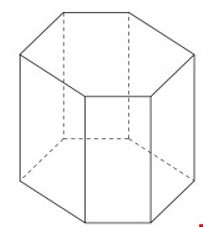
A. 6
B. 10
C. 12
D. 18
Đáp án: C
Tổng số cạnh của một đáy bằng 6
Tổng số cạnh của hai đáy là 12
Bài 5. Cho hình lăng trụ đứng ngũ giác ABCDE.A’B’C’D’E’ có bao nhiêu mặt phẳng vuông góc với mặt phẳng (ABCDE)
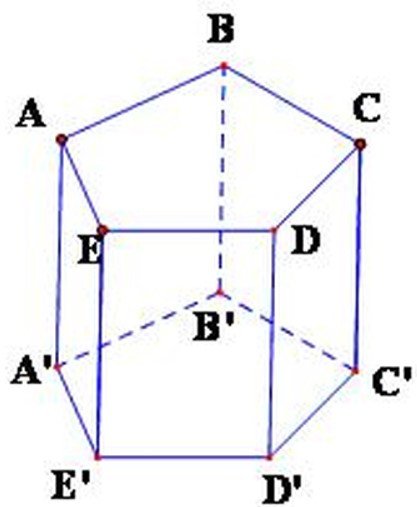
A. 3
B. 5
C. 7
D. 4
Mặt phẳng vuông góc với mặt phẳng (ABCDE) bao gồm :
5 mặt : mp(AEE’A’); mp(EDD’E’);
mp(DCC’D’); mp(CBB’C’); mp(ABB’A’)
Bài 6: Số cạnh bên của hình dưới đây là bao nhiêu
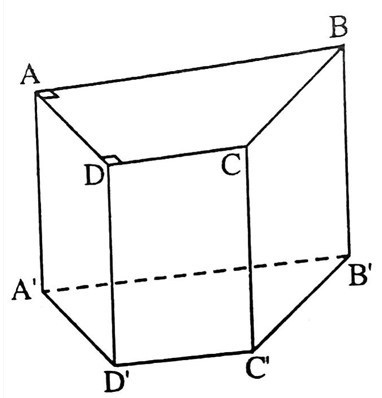
A. 4
B. 5
C. 6
D. 8
Đáp án: A
Hình trên có tất cả là 4 cạnh bên AA’, BB’, CC’, DD’.
Bài 7: Số mặt bên của hình lăng trụ đứng sau :
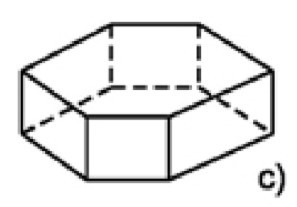
A. 5
B. 6
C. 7
D. 8
Đáp án: B
Số mặt bên của hình lăng trụ trên là 6 mặt
Bài 8: Cho hình lăng trụ đứng sau hãy tính tổng các mặt của hình đó
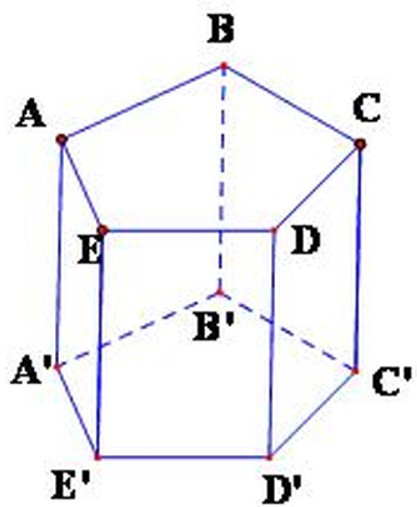
A. 5
B. 6
C. 7
D. 8
Đáp án: C
Tổng số mặt của lăng trụ trên là 7 mặt ( trong đó bao gồm 5 mặt bên và hai mặt đáy)
Bài 9: Các mặt bên của hình lăng trụ đứng là:
A. Các hình bình hành
B. Các hình thang cân
C. Các hình chữ nhật
D. Các hình vuông
Đáp án: C
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Bài 10: Các cạnh bên của hình lăng trụ đứng
A. Song song với nhau
B. Bằng nhau
C. Vuông góc với hai đáy
D. Có cả ba tính chất trên
Đáp án: D
Hình lăng trụ đứng có các mặt bên là những hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau
Bài tập vận dụng
Bài 1: Hãy kể tên các đỉnh, cạnh, mặt, chiều cao của hình lăng trụ đứng tam giác sau:
Hướng dẫn giải
Hình lăng trụ đứng tam giác ABC.DEF có:
- Các đỉnh: A, B, C, D, E, F.
- Các cạnh:
+ Cạnh đáy: AB, BC, CA, DE, EF, FD;
+ Cạnh bên: AD, BE, CF;
- Các mặt : Đáy dưới là tam giác ABC, đáy trên là tam giác DEF;
Các mặt bên là các hình chữ nhật: ADEB, BEFC, CFDA;
- Chiều cao là độ dài một cạnh bên: AD hoặc BE hoặc CF.
Bài 2: Tính diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác biết, đáy của nó là tam giác vuông và các kích thước như hình vẽ (đơn vị của các cạnh là cm).
Hướng dẫn giải
Ta tính chu vi đáy là tam giác ABC: C = 3 + 4 + 5 = 12 (cm), chiều cao h = 6 cm.
Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.DEF là:
Sxq = C . h = 12 . 6 = 72 (cm2).
Ta tính diện tích đáy (cm2).
Thể tích của hình lăng trụ đứng tam giác ABC.DEF là:
V = S.h = 6 . 6 = 36 (cm3).
Bài 3: Tính diện tích xung quanh và thể tích của lăng trụ đứng tứ giác, biết đáy của nó là hình chữ nhật (độ dài các cạnh đơn vị cm).
Hướng dẫn giải
Ta tính chu vi đáy C = 2(1 + 3 ) = 8 (cm), chiều cao h = 5 cm
Diện tích của hình lăng trụ đứng tứ giác này là: Sxq = C . h = 8 . 5 = 40 (cm2).
Ta tính diện tích đáy S = 1 . 3 = 3 (cm2)
Thể tích hình lăng trụ đứng tứ giác là: V = S . h = 3 . 5 = 15 (cm3).
Bài 4: Tính chiều cao của hình lăng trụ đứng ABCD.EFGH, biết rằng đáy ABCD là hình thoi có các đường chéo AC = 10cm,BD = 24cm và diện tích toàn phân bằng 1280cm2
Lời giải:
Áp dụng công thức: Stp = Sxq + 2Sd
Hay Sxq = Stp - 2Sd = 1280 - 2.1/2.1024
= 1280 - 240 = 1040( cm2 )
Vì đáy ABCD là hình thoi nên AC vuông góc với BD tại O (tính chất về đường chéo của hình thoi)
Áp dụng định lý Py – ta – go vào tam giác BOC vuông tại O ta được:
BC2 = BO2 + OC2 ⇒ BC2 = 122 + 52 = 132 ⇔ BC = 13( cm )
Chu vi đáy là 2p = 4.13 = 52( cm )
Áp dụng công thức Sxq = 2p.h
Bài 5: Một trại hè có dạng hình lăng trụ đứng đáy tam giác, thể tích hình không gian bên trong là 2,16( cm3 ). Biết chiều dài lều AD = 2,4( cm ), chiều rộng của lều là 1,2cm. Tính chiều cao AH của lều?
Lời giải:
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có:
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )
Bài 6. Cho hình lăng trụ ngũ giác ABCDE.A’B’C’D’E’.
a) Kể tên các mặt bên.
b) Kể tên các đỉnh.
c) Kể tên các mặt đáy.
d) Kể tên các cạnh song song và bằng nhau.
Lời giải:
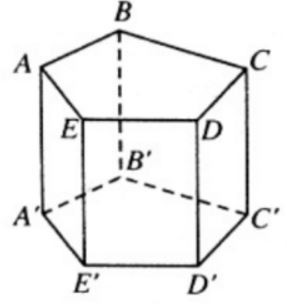
a) Các mặt bên là mặt ABB’A’; mặt BCC’B’; mặt CDD’C’; mặt DEE’D’; mặt AEE’A’
b) Tên các đỉnh là A; B; C; D; E; A’; B’; C’; D’ và E’
c) Hai mặt đáy là mặt ABCDE và mặt A’B’C’D’E’.
d) Tên các cạnh song song và bằng nhau.
+ Các cạnh AA’; BB’; CC’; DD’ và EE’ là các cạnh bên song song và bằng nhau.
+ AB song song và bằng A’B’.
+ BC song song và bằng B’C’
+ CD song song và bằng C’D’.
+ DE song song và bằng D’E’.
+ AE song song và bằng A’E’
Bài 7. Cho hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có đáy ABCD là hình bình hành.
a) Kể tên các đường thẳng vuông góc với mặt phẳng (ABCD).
b) Hình này có bao nhiêu cạnh bên?
c) Kể tên các cạnh đáy?
d) Những cặp mặt nào vuông góc với nhau.
Lời giải:
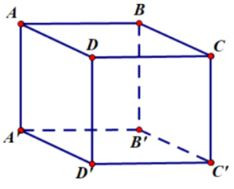
a) Các đường thẳng vuông góc với mặt phẳng (ABCD) là AA’; BB’; CC’ và DD’.
b) Hình này có 4 cạnh bên là: AA’; BB’; CC’ và DD’.
c) Các cạnh đáy là AB; BC; CD; DA; A’B’; B’C’; C’D’ và D’A’.
d) Những cặp mặt vuông góc với nhau:
+ Mặt (ABB’A’) và (ABCD) hoặc mặt (ABB’A’) và (A’B’C’D’).
+ Mặt ( BCC’B’) và (ABCD) hoặc mặt (BCC’B’) và (A’B’C’D’).
+ Mặt (CDD’C’) và (ABCD) hoặc mặt (CDD’C’) và (A’B’C’D’).
+ Mặt (DAA’D’) và (ABCD) hoặc mặt (DAA’D’) và (A’B’C’D’).