Thể tích khối lăng trụ: Công thức tính và bài tập vận dụng

nguyễn thương Ngày: 19-11-2024 Tổng hợp kiến thức

Tải xuống 6 4 K 11

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ tài liệu Thể tích khối lăng trụ: Công thức tính và bài tập vận dụng, tài liệu bao gồm đầy đủ lí thuyết và các dạng bài tập Thể tích khối lăng trụ có đáp án và lời giải chi tiết, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Thể tích khối lăng trụ: Công thức tính và bài tập vận dụng

1. Định nghĩa:

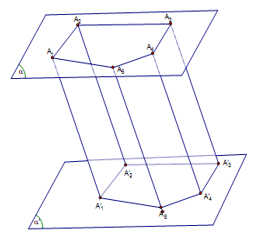
Cho hai mặt phẳng song song $(α)$ , $(α^{'})$ . Trên $(α)$ lấy đa giác lồi $A_{1} A_{2} .... A_{n}$ , qua các đỉnh của đa giác này dựng các đường thẳng song song với nhau cắt $(α^{'})$ tại ${A_{1}}^{'}, {A_{2}}^{'}, ...., {A_{n}}^{'}$

Hình gồm hai đa giác $A_{1} A_{2} .... A_{n}$ , ${A_{1}}^{'} {A_{2}}^{'} .... {A_{n}}^{'}$ và các hình bình hành $A_{1} A_{2} {A_{2}}^{'} {A_{1}}^{'}, A_{2} A_{3} {A_{3}}^{'} {A_{2}}^{'} ...., A_{n} A_{1} {A_{1}}^{'} {A_{n}}^{'}$ gọi là hình lăng trụ kí hiệu là $A_{1} A_{2} .... A_{n} . {A_{1}}^{'} {A_{2}}^{'} .... {A_{n}}^{'}$

Tài liệu VietJack

2. Các lăng trụ đặc biệt

a) Lăng trụ đứng: Là lăng trụ có cạnh bên vuông góc với đáy. Các mặt bên là các hình chữ nhật. Cạnh bên bằng đường cao của lăng trụ.

b) Lăng trụ đều: Là lăng trụ đứng và có đáy là đa giác đều. Các mặt bên của lăng trụ đều là các hình chữ nhật và bằng nhau.

c) Hình hộp: Là hình lăng trụ có đáy là hình bình hành.

+) 6 mặt của hình hộp là các hình bình hành.

+) Hai mặt đối diện song song và bằng nhau.

+) Bốn đường chéo của hình hộp đồng quy tại trung điểm của mỗi đường.

d) Hình hộp chữ nhật: là hình hộp có 6 mặt đều là các hình chữ nhật.

e) Hình lập phương: Là hình hộp có 6 mặt đều là các hình vuông (bằng nhau).

3. Công thức thể tích:

a) Thể tích khối lăng trụ

$V_{L T} = S . h$

với: S: Diện tích đáy

h: Chiều cao.

b) Thể tích khối hộp chữ nhật

$V = a . b . c$

với a, b, c là ba kích thước.

c) Thể tích khối lập phương

$V = a^{3}$

Trong đó a là độ dài cạnh.

4. Phương pháp tính thể tích khối lăng trụ

Bước 1: Xác định và tính chiều cao của khối đa diện

+) Trong nhiều trường hợp, chiều cao của khối đa diện được cho ngay từ đầu bài (chiều cao cho trực tiếp), nhưng cũng có trường hợp việc xác định phải dựa vào các định lí về quan hệ vuông góc (chiều cao cho gián tiếp), hay dùng nhất là: định lí 3 đường vuông góc, các định lí về điều kiện để một đường thẳng vuông góc với một mặt phẳng, …

+) Tính độ dài chiều cao: Sử dụng định lí Pitago, hoặc nhờ hệ thức lượng trong tam giác vuông, tỉ số lượng giác trong tam giác vuông, định lý cosin, …

+) Có thể tính chiều cao bằng cách chuyển về bài toán tìm khoảng cách từ một điểm đến một mặt phẳng.

Nếu $O A / / (α)$ thì $d (O, (α)) = d (A, (α))$

Nếu $O A \cap (α) = \{I\}$ thì $\frac{d (O, (α))}{d (A, (α))} = \frac{I O}{I A}$ (định lý Ta-lét)

Bước 2: Tìm diện tích đáy bằng các công thức.

Bước 3: Sử dụng công thức tính thể tích.

5. Bài tập tự luyện

Câu 1: Cho lăng trụ đứng ABC. A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a, AA’ = 2a. Thể tích khối lăng trụ ABC. A’B’C’ là

A. $\frac{2 a^{3}}{3}$

B. $2 a^{3}$

C. $\frac{a^{3}}{3}$

D. $a^{3}$

Lời giải

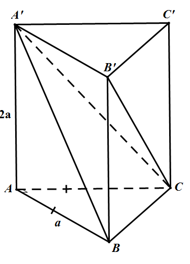
Tài liệu VietJack

Chọn D

Ta có chiều cao của lăng trụ là AA’ = 2a.

Diện tích đáy là:

$S_{A B C} = \frac{1}{2} A B . A C = \frac{1}{2} . a . a = \frac{a^{2}}{2}$

Thể tích khối lăng trụ là:

$V_{A B C . A' B' C'} = S_{A B C} . A A' = \frac{a^{2}}{2} .2 a = a^{3}$

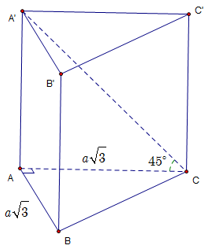
Câu 2: Cho lăng trụ đứng tam giác ABC. A’B’C’ có đáy là tam giác vuông cân tại A, cạnh $A B = a \sqrt{3}$ , góc giữa A’C và (ABC) bằng $45 °$ . Tính thể tích của khối lăng trụ.

A. $\frac{3 \sqrt{3}}{2} a^{3} .$

B. $a^{3} .$

C. $3 \sqrt{3} a^{3} .$

D. $\frac{a^{3}}{2} .$

Lời giải

Chọn A

Tài liệu VietJack

Câu 3: Tính thể tích của hình lập phương có độ dài đường chéo bằng $\sqrt{12}$ .

A. 8

B. 24

C. 12

D. 16

Hướng dẫn giải

Chọn A.

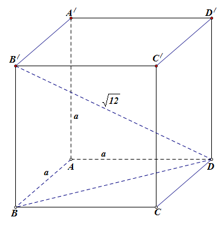
Tài liệu VietJack

Đặt AB = a. Vì đáy là hình vuông $\Rightarrow B D = a \sqrt{2}$

Vì vuông tại B nên $B^{'} D^{2} = B {B^{'}}^{2} + B D^{2}$

$12 = a^{2} + 2 a^{2}$

$\Leftrightarrow$ a = 2.

Vậy thể tích khối lập phương ABCD. A’B’C’D’ là:

$V_{A B C D . A' B' C' D'} = a^{3} = 2^{3} = 8.$

Câu 4: Cho hình lăng trụ tam giác ABC. A’B’C’ có BB’ = a, góc giữa đường thẳng BB’ và mặt phẳng (ABC) bằng $60 °$ , tam giác ABC vuông tại C và góc bằng $60 °$ . Hình chiếu vuông góc của điểm B’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Tính thể tích khối lăng trụ ABC. A’B’C’ theo a.

Lời giải

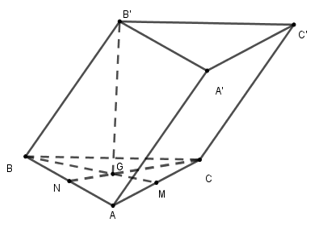
Tài liệu VietJack

Gọi G là trọng tâm của tam giác ABC. Khi đó $B^{'} G ⊥ (A B C)$

Tam giác B’BG vuông tại G nên góc B’BG là góc nhọn.

BG là hình chiếu vuông góc của đường thẳng BB’ trên (ABC) nên góc giữa BB’ và (ABC) bằng góc giữa BB’ và BG và bằng góc B’BG, bằng $60 °$ .

Tam giác B’BG vuông tại G nên:

$B^{'} G = B B^{'} . \sin \hat{B^{'} B G} = a . \sin 60 ° = \frac{a \sqrt{3}}{2}$

$B G = B B^{'} . \cos \hat{B^{'} B G} = a . c os 60 ° = \frac{a}{2}$

Gọi M là trung điểm của AC, ta có

$B M = \frac{3}{2} B G = \frac{3 a}{4} .$

Đặt AB = 2x

Vì tam giác ABC vuông tại C ta có :

+) $A C = A B . \cos \hat{B A C} = 2 x . \cos 60^{o}$

$= x \Rightarrow C M = \frac{x}{2}$

+) $B C = A B . \sin \hat{B A C} = 2 x . \sin 60^{0}$

$= 2 x . \frac{\sqrt{3}}{2} = x \sqrt{3}$

Tam giác BCM vuông tại C nên

$B M^{2} = C B^{2} + C M^{2} \Leftrightarrow \frac{9 a^{2}}{16} = {(x \sqrt{3})}^{2} + {(\frac{x}{2})}^{2} = \frac{13 x^{2}}{4} \Rightarrow x = \frac{3 a \sqrt{13}}{26}$

Diện tích tam giác ABC là :

$S_{A B C} = \frac{1}{2} . C A . C B = \frac{1}{2} . x . x \sqrt{3} = \frac{9 a^{2} \sqrt{3}}{104}$

Vậy thể tích khối lăng trụ đã cho là $V = B^{'} G . S_{A B C} = \frac{27 a^{3}}{208}$

Tài liệu có 6 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm