Tailieumoi.vn xin giới thiệu tài liệu về Giới hạn của hàm số thuộc chương trình Toán 11. Chuyên đề gồm đầy đủ lý thuyết, phương pháp giải các dạng bài tập và trên 200 bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 11.
Giới hạn của hàm số: Lý thuyết và các dạng bài tập
I. Lý thuyết về Giới hạn của hàm số
1. Giới hạn hữu hạn
+) Cho khoảng chứa điểm và hàm số xác định trên hoặc trên
khi và chỉ khi với dãy số bất kì, và , ta có
.
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi dãy số \((xn) bất kì, và ,ta có .
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, và , ta có
.
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, , thì .
+) Cho hàm số xác định trên khoảng .
khi và chỉ khi với dãy số bất kì, , thì .
2. Giới hạn vô cực
Sau đây là hai trong số nhiều loại giới hạn vô cực khác nhau:
+) Cho hàm số xác định trên khoảng , khi và chỉ khi với dãy số bất kì, , thì ta có
+) Cho khoảng chứa điểm và hàm số xác định trên hoặc trên
và chỉ khi với dãy số bất kì, và thì ta có: .
Nhận xét: có giới hạn khi và chỉ khi có giới hạn .
3. Các giới hạn đặc biệt
a) ;
b) ;
c) ;
d) ( là hằng số);
e) , với nguyên dương;
f) , nếu là số lẻ;
g) , nếu là số chẵn.
4. Định lí về giới hạn hữu hạn
Định lí 1.
a) Nếu và thì:
;
;
;
= (nếu ).
b) Nếu và , thì và
Chú ý: Định lí 1 vẫn đúng khi hoặc .
Định lí 2.
khi và chỉ khi f(x) = .
5. Quy tắc về giới hạn vô cực
a) Quy tắc giới hạn của tích
+ Nếu và thì được cho trong bảng sau:
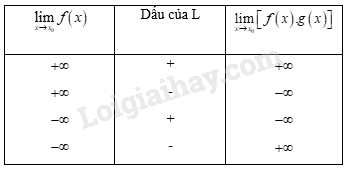
b) Quy tắc tìm giới hạn của thương
+ Nếu và và hoặc với mọi , trong đó là một khoảng nào đó chứa thì được cho trong bảng sau:
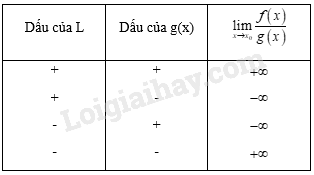
II. Các dạng bài tập về tìm giới hạn của hàm số
Phần 1: Cách tìm giới hạn của hàm số bằng định nghĩa cực hay
Ta sử dụng phương pháp chung để làm các bài toán dạng này.
Bài 1: Tìm các giới hạn sau:
Hướng dẫn:
Ta có:
Bài 2: Xét xem các hàm số sau có giới hạn tại các điểm chỉ ra hay không? Nếu có hay tìm giới hạn đó?
Hướng dẫn:
Bài 3: Tìm m để các hàm số:
Hướng dẫn:
Ta có:
Bài 4: Tìm các giới hạn sau:
Hướng dẫn:
Ta có:
Bài 5: Xét xem các hàm số sau có giới hạn tại các điểm chỉ ra hay không? Nếu có hay tìm giới hạn đó?
Hướng dẫn:
Ta có:
Vậy hàm số f(x) không có giới hạn khi x → 0.
Bài 6: Tìm m để các hàm số:
Hướng dẫn:
Ta có:
Bài 7: Tìm giới hạn các hàm số sau:
Hướng dẫn:
Ta có
Bài 8: Tìm giới hạn các hàm số sau:
Hướng dẫn:
Phần 2: Cách tìm giới hạn hàm số dạng 0/0, dạng vô cùng trên vô cùng cực hay
Tìm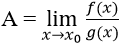 
trong đó f(x0) = g(x0) = 0
Dạng này ta gọi là dạng vô định 0/0
Để khử dạng vô định này ta sử dụng định lí Bơzu cho đa thức:
Định lí: Nếu đa thức f(x) có nghiệm x = x0 thì ta có :f(x) = (x-x0)f1(x)
* Nếu f(x) và g(x) là các đa thức thì ta phân tích
f(x) = (x-x0)f1(x)và : g(x) = (x-x0)g1(x).
Khi đó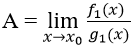 
, nếu giới hạn này có dạng 0/0 thì ta tiếp tục quá trình như trên.
Bài 1: Tìm các giới hạn sau: 
Hướng dẫn:
Ta có: 
Bài 2: Tìm giới hạn sau: 
Hướng dẫn:
Ta có:
Bài 3: 
Hướng dẫn:
Đặt t = x - 1 ta có:
Bài 4: 
Hướng dẫn:
Ta có:
Nên ta có B = 1 + 1 + 1 = 3
Bài 5: 
Hướng dẫn:
Ta có:
Vậy A = -2/3
Bài 6: 
Hướng dẫn:
Ta có:
Mà
Phần 3: Cách tìm giới hạn hàm số dạng 0 nhân vô cùng cực hay
Bài toán: Tính giới hạn
Ta có thể biến đổi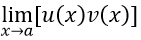 
về dạng 0/0 hoặc ∞/∞ rồi dùng các phương pháp tính giới hạn của hai dạng kia để làm.
Tuy nhiên, trong nhiều bài tập ta chỉ cần biến đổi đơn giản như đưa biểu thức vào trong (hoặc ra ngoài) dấu căn, quy đồng mẫu thức …. Là có thể đưa về dạng quen thuộc.
Bài 1: Tính giới hạn: 
Hướng dẫn:
Ta có:
Bài 2: Tính giới hạn: 
Hướng dẫn:
Ta có:
Bài 3: Tính giới hạn: 
Hướng dẫn:
Bài 4: Tính giới hạn: 
Hướng dẫn:
Bài 5: Tính giới hạn: 
Hướng dẫn:
Bài 6: Tính giới hạn: 
Hướng dẫn:
(chia cả tử và mẫu cho x3)
Bài 7: Tính giới hạn: 
Hướng dẫn:
Phần 4: Tìm giới hạn hàm số dạng vô cùng trừ vô cùng, vô cùng trên vô cùng
Những dạng vô định này ta tìm cách biến đổi đưa về dạng ∞/∞
Bài 1: Tìm các giới hạn sau:
Hướng dẫn:
Ta có:
Bài 2: 
Hướng dẫn:
Bài 3: 
Hướng dẫn:
Bài 4: 
Hướng dẫn:
Bài 5: 
Hướng dẫn:
Bài 6: 
Hướng dẫn:
Phần 5: Cách tính giới hạn của hàm số có chứa căn thức cực hay, chi tiết
- Đối với giới hạn hàm số dạng vô định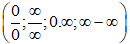 
, sử dụng các phép biến đổi liên hợp
- Đối với giới hạn hàm số tại vô cực, sử dụng phương pháp chia cả tử và mẫu cho lũy thừa bậc cao nhất của x.
Ví dụ 1: Tìm các giới hạn sau:
Hướng dẫn giải:
Ví dụ 2: Tìm các giới hạn sau:
Hướng dẫn giải:
Ví dụ 3: Tìm các giới hạn sau:
Hướng dẫn giải:
Ta dễ dàng thấy đây là dạng vô định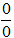 
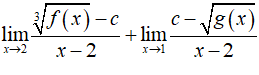
và tử số có hai căn thức khác loại, nên ta phải thêm bớt một hằng số c sao cho đưa được về dạng 
và mỗi giới hạn đều tính được giới hạn khi khử được dạng vô định bằng phương pháp nhân lượng liên hợp.
Kỹ thuật 1: Thay x = 2 vào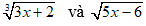 
đều bằng 2. Suy ra 2 là giá trị ta cần thêm bớt.
Kỹ thuật 2: Cho x – 2 = 0 ⇔ x = 2 sau đó giải hệ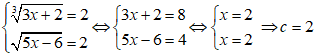 
là giá trị cần thêm bớt.
tương tự câu b) thay x = 2 vào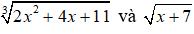 
đều bằng 3. Như vậy 3 là giá trị cần thêm và bớt, cụ thể:
Ví dụ 4: Tìm các giới hạn sau:
Hướng dẫn giải:
Phần 6: Cách tính giới hạn của hàm số có chứa trị tuyệt đối cực hay, chi tiết
a) Dạng 1: Tìm giới hạn của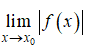 
với f(x) là các hàm đa thức, phân thức,…
- Bước 1: Tính giới hạn của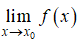 
(đưa về các giới hạn đã biết để tính)
- Bước 2: Suy ra 
b) Dạng 2: Tìm giới hạn của 
- Bước 1: Xét dấu của các biểu thức trong dấu giá trị tuyệt đối để bỏ dấu trị tuyệt đối
● Sử dụng tính chất của giá trị tuyệt đối: 
● Sử dụng định nghĩa về giới hạn một bên: 
- Bước 2: Thực hiện tính toán, đưa về các giới hạn của đa thức, phân thức,… thường gặp rồi tìm giới hạn.
Ví dụ 1: Tính các giới hạn sau
Hướng dẫn giải:
a) Ta có x →(-3)+ suy ra x + 3 > 0 thì 2x + 6 = 2(x + 3) > 0
Do đó |2x + 6| = 2x + 6
b) Ta có x →(-5)- suy ra x + 5 < 0 thì 3x + 15 = 3(x + 5) < 0
Do đó |3x + 15| = –3x – 15
Ví dụ 2: Tính các giới hạn sau
Hướng dẫn giải:
Ví dụ 3: Giá trị của giới hạn 
Hướng dẫn giải:
Ta tính giới hạn như hàm phân thức bình thường.
Đáp án C
Phần 7: Cách tính giới hạn của hàm số lượng giác cực hay, chi tiết
- Áp dụng giới hạn đặc biệt: 
- Các bước tìm giới hạn hàm số lượng giác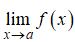 
với f(x) là hàm số lượng giác
● Bước 1: Sử dụng các công thức lượng giác cơ bản, công thức nhân đôi, công thức cộng, công thức biến đổi,… (đã được học ở chương 6 Đại số 10) để biến đổi hàm số lượng giác f(x) về cùng dạng giới hạn đặc biệt nêu trên.
● Bước 2: Áp dụng các định lý về giới hạn để tìm giới hạn đã cho.
Ví dụ 1: Cho a và b là hai số thực khác 0. Khi đó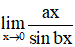 
bằng:
Hướng dẫn giải:
Đáp án C
Ví dụ 2: Tính các giới hạn sau:
Hướng dẫn giải:
Ví dụ 3: Tính các giới hạn sau (với a là số thực khác 0)
Hướng dẫn giải:
(áp dụng công thức cộng: sin(a-b) = sina.cosb-cosa.sinb)
Phần 8: Cách chứng minh phương trình có nghiệm cực hay, chi tiết
+) Áp dụng định lý: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0, thì phương trình f(x) = 0 có ít nhất 1 nghiệm nằm trong khoảng (a; b).
+) Các bước làm bài chứng minh phương trình có nghiệm.
- Bước 1: Biến đổi phương trình cần chứng minh về dạng f(x) = 0.
- Bước 2: Tìm 2 số a và b (a < b) sao cho f(a) . f(b) < 0
- Bước 3: Chứng minh hàm số y = f(x) liên tục trên đoạn [a; b].
Từ đó suy ra phương trình f(x) = 0 có ít nhất một nghiệm thuộc (a; b).
Lưu ý: Các bước trên có thể thay đổi thứ tự.
+) Một số chú ý:
- Nếu f(a).f(b) ≤ 0 thì phương trình có ít nhất 1 nghiệm thuộc [a; b].
- Nếu hàm số f(x) liên tục trên [a; + ∞) và có f(a) .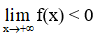 
< 0 thì phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc (a; +∞).
- Nếu hàm số f(x) liên tục trên (-∞; a] và có f(a) .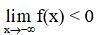 
< 0 thì phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc (-∞; a).
Ví dụ 1: Chứng minh rằng phương trình x3 + x - 1 = 0 có nghiệm.
Hướng dẫn giải:
Đặt f(x) = x3 + x - 1
Hàm f(x) là hàm đa thức nên f(x) liên tục trên R (định lý cơ bản về tính liên tục)
Suy ra hàm f(x) liên tục trên đoạn [0; 1] (vì [0; 1] ⊂R) (1)
Ta có: f(0) = 03 + 0 – 1 = - 1 ; f(1) = 13 + 1 – 1 = 1
⇒ f(0) . f(1) = - 1. 1 = - 1 < 0 (2)
Từ (1) và (2) suy ra f(x) = 0 có ít nhất 1 nghiệm thuộc (0; 1) (tính chất hàm số liên tục).
Vậy phương trình x3 + x - 1 = 0 có nghiệm (đpcm).
Ví dụ 2: Chứng minh 4x4 + 2x2 - x - 3 = 0 có ít nhất hai nghiệm thuộc khoảng (-1; 1).
Hướng dẫn giải:
+ Đặt f(x) = 4x4 + 2x2 - x - 3
Vì f(x) là hàm đa thức nên f(x) liên tục trên R.
Suy ra f(x) liên tục trên các đoạn [-1 ; 0] và [0; 1].
+ Ta có: f(-1) = 4.(-1)4 + 2.(-1)2 - (-1) - 3 = 4
f(0) = 4.0 + 2.0 - 0 - 3 = -3
f(1) = 4.14 + 2.12 - 1 - 3 = 2
+ Vì f(-1).f(0) = 4.(-3) = -12 < 0 nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc (-1; 0)
Vì f(0) . f(1) = -3 . 2 = -6 < 0 nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc (0; 1)
Mà hai khoảng (-1; 0) và (0; 1) không giao nhau. Từ đó suy ra phương trình đã cho có ít nhất hai nghiệm thuộc (-1; 1). (đpcm)
Ví dụ 3: Chứng minh rằng phương trình x5 - 5x3 + 4x - 1 = 0 có đúng 5 nghiệm.
Hướng dẫn giải:
Đặt f(x) = x5 - 5x3 + 4x - 1 thì f(x) liên tục trên R (vì f(x) là hàm đa thức).
Ta có:
Vì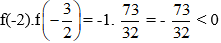 
nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc 
Vì 
nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng 
Vì 
nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng 
Vì 
nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng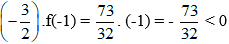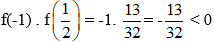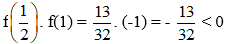 
Vì f(1) . f(3) = -1 . 119 = -119 < 0 nên phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng (1; 3).
Do các khoảng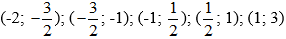 
không giao nhau nên phương trình f(x) = 0 có ít nhất 5 nghiệm.
Mà phương trình f(x) = 0 có bậc là 5, nên nó có không quá 5 nghiệm
Vậy phương trình f(x) = 0 có đúng 5 nghiệm (đpcm).
Ví dụ 4: Chứng minh rằng phương trình (m2 - m + 3)x2n - 2x - 4 = 0 với n ∈ N* luôn có ít nhất 1 nghiệm âm với mọi giá trị của tham số m.
Hướng dẫn giải:
Đặt f(x) = (m2 - m + 3)x2n - 2x - 4
Ta có:
Mặt khác hàm số f(x) xác định là liên tục trên R nên hàm số liên tục trên đoạn [-2; 0]
Do đó phương trình f(x) = 0 có ít nhất 1 nghiệm thuộc khoảng (-2; 0).
Vậy phương trình đã cho luôn có ít nhất 1 nghiệm âm với mọi giá trị của tham số m.
Ví dụ 5: Chứng minh rằng với mọi a, b, c phương trình x3 + ax2 + bx + c = 0 luôn có nghiệm.
Hướng dẫn giải:
Đặt f(x) = x3 + ax2 + bx + c thì f(x) liên tục trên R (vì f(x) là hàm đa thức).
Ta có: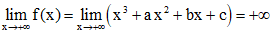 
⇒∃ x1 > 0 để f(x1) > 0
Tương tự: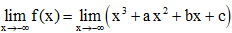 
⇒∃ x2 < 0 để f(x2) < 0
Như vậy có x1 ; x2 để f(x1) . f(x2) < 0 suy ra phương trình có nghiệm x ∈ (x1; x2)
Vậy phương trình đã cho luôn có nghiệm với mọi a, b, c.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
