Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập

diep4602 Ngày: 26-05-2023 Tổng hợp kiến thức

1 K

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập, tài liệu bao gồm có định nghĩa, công thức tính và các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập

1. Khái niệm nguyên hàm lnx

Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K. Nguyên hàm của lnx được tính như sau:

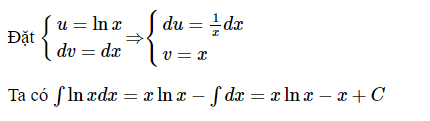
Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 1)

2. Bảng công thức nguyên hàm của ln(x)

3. Các dạng bài tập về nguyên hàm Inx thường gặp

Đối với bài tập về nguyên hàm của Inx sẽ có nhiều dạng khác nhau, mỗi dạng sẽ có những cách giải riêng dựa vào công thức trên để tìm đáp án. Cụ thể:

Dạng 1: Nguyên hàm In(x+1)

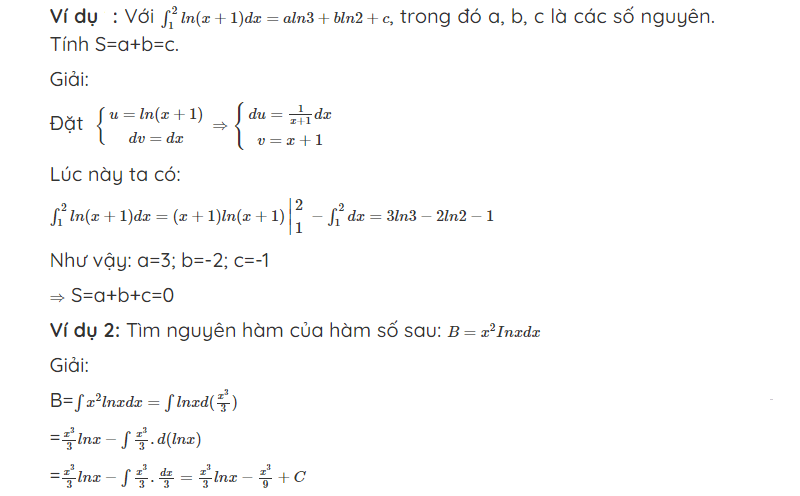
Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 3)

Dạng 2: Nguyên hàm 1+In/x

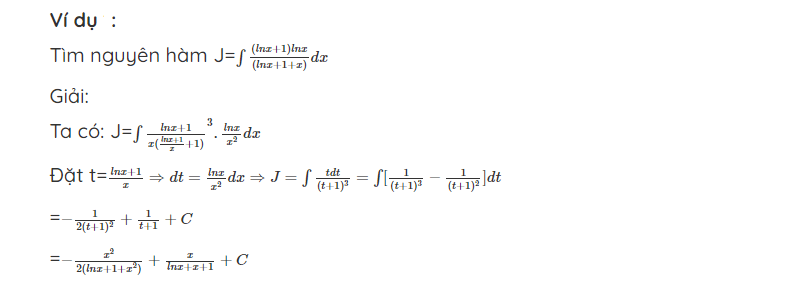
Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 4)

Dạng 3: Nguyên hàm của In(ax+b)

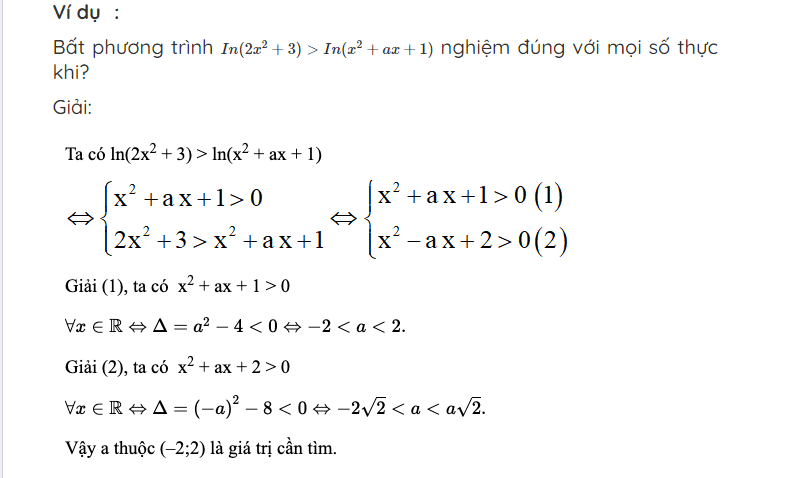
Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 5)

Dạng 4: Nguyên hàm của In(x2 +1)dx

Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 6)

Dạng 5: Nguyên hàm của hàm số f(x)=In/x

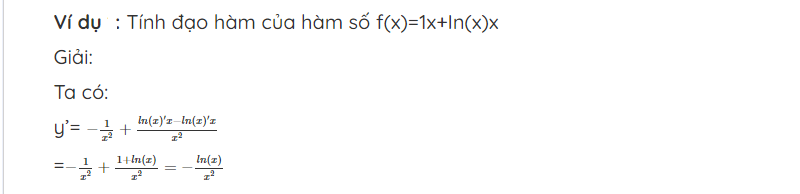
Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 7)

Dạng 6: Tính nguyên hàm của In(Inx)/x

Nguyên hàm lnx: Định nghĩa, công thức tính và các dạng bài tập (ảnh 8)

4. Bài tập tự luyện

Bài tập 1:

Tìm nguyên hàm của hàm số sau: ∫xlnx.dx

Bài tập 2:

Bài tập 3: Tính nguyên hàm của hàm số $A = \int {x\ln xdx}$

Hướng dẫn giải

Cách 1:

Đặt $\left\{ {\begin{array}{*{20}{c}} {u = \ln x} \\ {xdx = dv} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = \dfrac{1}{x}dx} \\ {v = \dfrac{{{x^2}}}{2}} \end{array}} \right.$

Khi đó nguyên hàm được tính như sau:

$A = \int {x\ln xdx} = \frac{{{x^2}}}{1}\ln x - \int {\frac{{{x^2}}}{2}.\frac{{dx}}{x} = \frac{{{x^2}}}{2}\ln x} - \frac{{{x^2}}}{4} + C$

Cách 2:

$\begin{matrix} A = \int {x\ln xdx} \hfill \\ = \int {\ln xd\left( {\dfrac{{{x^2}}}{2}} \right)} = \dfrac{{{x^2}}}{1}\ln x - \int {\dfrac{{{x^2}}}{2}.d\left( {\ln x} \right)} \hfill \\ = \dfrac{{{x^2}}}{1}\ln x - \int {\dfrac{{{x^2}}}{2}.\dfrac{{dx}}{x}} = \dfrac{{{x^2}}}{2}\ln x - \dfrac{{{x^2}}}{4} + C \hfill \\ \end{matrix}$

Bài tập 4: Tìm nguyên hàm của hàm số sau: $B = \int {{x^2}\ln xdx}$

Hướng dẫn giải

Cách 1:

Đặt $\left\{ {\begin{array}{*{20}{c}} {u = \ln x} \\ {{x^2}dx = dv} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {du = \dfrac{1}{x}dx} \\ {v = \dfrac{{{x^3}}}{3}} \end{array}} \right.$

Khi đó nguyên hàm được tính như sau:

$B = \int {{x^2}\ln xdx} = \frac{{{x^3}}}{3}\ln x - \int {\frac{{{x^3}}}{3}.\frac{{dx}}{x} = \frac{{{x^3}}}{3}\ln x} - \frac{{{x^3}}}{9} + C$

Cách 2:

$\begin{matrix} B = \int {{x^2}\ln xdx} = \int {\ln xd\left( {\dfrac{{{x^3}}}{3}} \right)} \hfill \\ = \dfrac{{{x^3}}}{3}\ln x - \int {\dfrac{{{x^3}}}{3}.d\left( {\ln x} \right)} \hfill \\ = \dfrac{{{x^3}}}{3}\ln x - \int {\dfrac{{{x^3}}}{3}.\dfrac{{dx}}{x} = \dfrac{{{x^3}}}{3}\ln x} - \dfrac{{{x^3}}}{9} + C \hfill \\ \end{matrix}$

Bài tập 5: Tình nguyên hàm của hàm số $C = \int {\ln \left( {x + \sqrt {1 + {x^2}} } \right)dx}$

Hướng dẫn giải

$\begin{matrix} C = \int {\ln \left( {x + \sqrt {1 + {x^2}} } \right)dx} \hfill \\ = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \int {xd\left[ {\ln \left( {x + \sqrt {1 + {x^2}} } \right)} \right]} \hfill \\ = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \int {\frac{{1 + \dfrac{x}{{\sqrt {1 + {x^2}} }}}}{{x + \sqrt {1 + {x^2}} }}.xdx} \hfill \\ = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \int {\dfrac{x}{{\sqrt {1 + {x^2}} }}dx} \hfill \\ = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \dfrac{1}{2}\int {\dfrac{{d\left( {{x^2} + 1} \right)}}{{\sqrt {1 + {x^2}} }}} \hfill \\ = x\ln \left( {x + \sqrt {1 + {x^2}} } \right) - \sqrt {1 + {x^2}} + C \hfill \\ \end{matrix}$