Tailieumoi.vn xin giới thiệu tới bạn đọc tài liệu về Cách tính thể tích hình hộp chữ nhật và các dạng bài tập, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Hình hộp chữ nhật, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Cách tính thể tích hình hộp chữ nhật và các dạng bài tập
A. Lý thuyết Thể tích Hình hộp chữ nhật
Ta có V = a.b.h
B. Bài tập Thể tích hình hộp chữ nhật
Bài tập trắc nghiệm
Câu 1: Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi cộng với chiều cao (cùng đơn vị đo). Đúng hay sai?
A. Đúng
B. Sai
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).
Vậy phát biểu trên là sai.
Câu 2: Một hình hộp chữ nhật có chiều dài là a, chiều rộng là b, chiều cao là c. Công thức tính thể tích V của hình hộp chữ nhật đó là:
A. V = (a + b) × c
B. V = a × b × c
C. V = a × b + c
D. V = (a + b) × 2 × c
Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).
Vậy công thức tính thể tích V của hình hộp chữ nhật đó là V = a × b × c.
Câu 3: Tính thể tích hình hộp chữ nhật có chiều dài là 17cm, chiều rộng là 9cm, chiều cao là 11cm.
A. 286cm3
B. 572cm3
C. 876cm3
D. 1683cm3
Thể tích hình hộp chữ nhật đó là:
17 × 9 × 11 = 1683 (cm3)
Đáp số: 1683cm3.
Câu 4: Điền số thích hợp vào ô trống:
Một hình hộp chữ nhật có chiều dài là 28m, chiều rộng là 15m và chiều cao bằng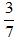 
chiều dài.
Vậy thể tích hình hộp chữ nhật đó là 
m3
Chiều cao của hình hộp chữ nhât là:
28 × 37 = 12 (m)
Thể tích hình hộp chữ nhật đó là:
28 × 15 × 12 = 5040 (m3)
Đáp số: 5040m3.
Vậy đáp án đúng điền vào ô trống là 5040.
Câu 5: Điền số thích hợp vào ô trống:
Thể tích hình hộp chữ nhật có chiều dài 23dm, chiều rộng 12dm và chiều cao 0,9m là m3.
Đổi 23dm = 2,3m; 12dm = 1,2m
Thể tích hình hộp chữ nhật đó là:
2,3 × 1,2 × 0,9 = 2,484 (m3)
Đáp số: 2,484m3.
Vậy đáp án đúng điền vào ô trống là 2,484.
Câu 6: Một bể nước hình hộp chữ nhật có các kích thước trong bể là chiều dài 3m; chiều rộng kém chiều dài 1,8m; chiều cao 1,5m. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước? (1 lít = 1dm3)
A. 5,4 lít
B. 81 lít
C. 5400 lít
D. 8100 lít
Chiều rộng của bể nước đó là:
3 − 1,8 = 1,2 (m)
Thể tích của bể nước đó là:
3 × 1,2 × 1,5 = 5,4 (m3)
5,4m3 = 5400dm3 = 5400 lít
Số lít nước bể có thể chứa được nhiều nhất bằng với thể tích của bể và bằng 5400 lít.
Đáp số: 5400 lít.
Câu 7: Một bể cá cảnh hình hộp chữ nhật có chiều dài 1,8m; chiều rộng 0,6m và chiều cao 0,9m. Hỏi người ta phải đổ vào trong bể cá đó bao nhiêu lít nước để lượng nước trong bể cao 0,6m?
A. 972 lít
B. 648 lít
C. 324 lít
D. 234 lít
Số lít nước cần đổ vào bể cá cảnh để lượng nước trong bể cao 0,6m là:
1,8 × 0,6 × 0,6 = 0,648 (m3)
0,648m3 = 648dm3 = 648 lít
Đáp số: 648 lít.
Câu 8: Điền số thích hợp vào ô trống:
Một hình hộp chữ nhật có thể tích 16m3, chiều dài là 3,2m và chiều rộng là 2m.
Vậy chiều cao của hình hộp chữ nhật đó là cm.
Diện tích đáy của hình hộp chữ nhật là:
3,2 × 2 = 6,4 (m)
Chiều cao của hình hộp chữ nhật đó là:
16 : 6,4 = 2,5 (m)
2,5m = 250cm
Đáp số: 250cm.
Vậy đáp án đúng điền vào ô trống là 250.
Câu 9: Một bể nước hình hộp chữ nhật có thể tích là 30dm3, chiều cao là 0,4m. Biết đáy bể có chiều rộng là 1,5dm. tính chiều dài của đáy bể.
A. 5dm
B. 7,5dm
C. 16dm
D. 20dm
Đổi 0,4m = 4dm
Diện tích đáy của bể nước đó là:
30 : 4 = 7,5 (dm3)
Chiều dài của đáy bể là:
7,5 : 1,5 = 5 (dm)
Đáp số: 5dm.
Câu 10: Điền số thích hợp vào ô trống (dạng thu gọn nhất có thể):
Một thùng hàng hình hộp chữ nhật có tỉ số giữa chiều dài và chiều rộng là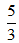 
. Biết chiều dài hơn chiều rộng 36cm và chiều cao của thùng hàng bằng trung bình cộng độ dài chiều rộng và chiều dài.
Vậy thể tích của thùng hàng đó là dm3.
Theo bài ra ta có sơ đồ:
Theo sơ đồ, hiệu số phần bằng nhau là:
5 − 3 = 2 (phần)
Giá trị một phần là:
36 : 2 = 18 (cm)
Chiều dài của thùng hàng là:
18 × 5 = 90 (cm)
Chiều rộng của thùng hàng là:
90 − 36 = 54 (cm)
Chiều cao của thùng hàng là:
(90 + 54) : 2 = 72 (cm)
Thể tích của thùng hàng đó là:
90 × 54 × 72 = 349920 (cm3)
349920cm3 = 349,92dm3
Đáp số: 349,92dm3.
Vậy đáp án đúng điền vào ô trống là 349,92.
Câu 11: Một bể nước dạng hình hộp chữ nhật có chiều dài 2m; chiều rộng 1,2m và chiều cao 1,4m. Hiện tại, lượng nước trong bể chiếm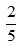 
thể tích của bể. Hỏi cần phải đổ thêm vào bể bao nhiêu lít nước để được đầy bề nước?
A. 134,4 lít
B. 201,6 lít
C. 1344 lít
D. 2016 lít
Thể tích của bể nước là:
2 × 1,2 × 1,4 = 3,36 (m3)
Thể tích nước đang có trong bể là:
3,36 × 25 = 1,344 (m3)
Thể tích cần đổ thêm vào bể để bể đầy nước là:
3,36 − 1,344 = 2,016 (m3)
Đổi 2,016m3 = 2016dm3 = 2016 lít
Đáp số: 2016 lít.
Câu 12: Điền số thích hợp vào ô trống:
Người ta thả 2 hòn đá có thể tích như nhau vào bể nước làm nước trong bể dâng cao thêm 1,4dm. Biết chiều dài bể là 80cm, chiều rộng của bể là 45cm.
Vậy thể tích mỗi hòn đá là cm3.
Đổi 1,4dm = 14cm
Thể tích của hai hòn đá là:
80 × 45 × 14 = 50400 (cm3)
Thể tích của mỗi hòn đá là:
50400 : 2 = 25200 (cm3)
Đáp số: 25200cm3.
Vậy đáp án đúng điền vào ô trống là 25200.
Câu 13: Một bể cá dạng hình hộp chữ nhật có chiều dài 90cm, chiều rộng là 50cm và chiều cao 75cm. Mực nước ban đầu trong bể cao 45cm. Người ta cho vào bể một hòn đá có thể tích 18dm3. Hỏi mực nước trong bể lúc này cao bao nhiêu xăng-ti-mét?
A. 49cm
B. 54cm
C. 63cm
D. 75cm
Đổi 18dm3 = 18000cm3
Diện tích đáy của bể cá là:
90 × 50 = 4500 (cm3)
Chiều cao mực nước tăng thêm là:
18000 : 4500 = 4 (cm)
Chiều cao mực nước lúc sau khi thả hòn đá là:
45 + 4 = 49 (cm)
Đáp số: 49cm.
Câu 14: Một cái bể hình hộp chữ nhật có chiều dài là 1,5m, chiều rộng là 1,2m và chiều cao 0,9m. Bể đã hết nước. Người ta đổ vào đó 30 gánh nước, mỗi gánh 45 lít. Hỏi mặt nước còn cách miệng bể bao nhiêu xăng-ti-mét?
A. 5cm
B. 15cm
C. 30cm
D. 75cm
Diện tích đáy của bể là:
1,5 × 1,2 = 1,8 (m3)
Thể tích lượng nước đã đổ vào bể là:
45 × 30 = 1350 (lít)
Đổi 1350 lít = 1350dm3 = 1,35m3
Chiều cao mực nước trong bể là:
1,35 : 1,8 = 0,75 (m)
Mặt nước còn cách miệng bể là:
0,9 − 0,75 = 0,15 (m)
0,15m = 15cm
Đáp số: 15cm.
Bài tập tự luận
Bài 1: Cho hình hộp chữ nhật ABCD.A1B1C1D1 có ABCD là hình vuông. Gọi O là giao điểm của AC và BD, O1 là giao điểm của A1C1 và B1D1. Chứng minh rằng:
a) BDD1B1 là hình chữ nhật.
b) OO1 ⊥ ( ABCD )
Lời giải:
a) Từ giả thiết ABCD.A1B1C1D1 là hình hộp chữ nhật nên các mặt bên ( BB1A1A ),( BB1C1C ) là hình chữ nhật, do đó ta có:
⇒ BB1 ⊥ mp( ABCD )
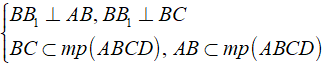
Mặt khác đường chéo BD ⊂ mp( ABCD ) và đi qua B nên:
BB1 ⊥ BD ⇒ Bˆ1BD = 900
Chứng minh tương tự như trên, ta cũng được: BB1D1ˆ = BDD1ˆ = 900
Điều đó chứng tỏ tứ giác BDD1B1 có ba góc vuông nên là hình chữ nhật.
b) Chứng minh tương tự như câu a, ta có tứ giác ACC1A1 là hình chữ nhật
Áp dụng tính chất đường chéo và các hình vuông ABCD, A1B1C1D1 ta được O là trung điểm của AC và BD và O1 là trung điểm của A1C1 và B1D1
⇒ OO1 là đường trung bình của các hình chữ nhật BDD1B1 và ACC1A1
Do đó: OO1//BB1//DD1//AA1//CC1
Suy ra
Bài 2: Các kích thức của hình hộp chữ nhật như trên hình vẽ. Tính độ dài của đoạn AC1 ?
Lời giải:
Vì ABCD.A1B1C1D1 là hình hộp chữ nên
CC1 ⊥ mp( ABCD ) ⇒ CC1 ⊥ AC hay tam giác ACC1 vuông tại C, đáy ABCD là hình chữ nhật nên tam giác ACD vuông tại D.
Áp dụng định lý Py – ta – go ta có:
Thay đẳng thức ( 1 ) vào ( 2 ) ta được:
AC12 = CD2 + AD2 + CC12 ⇒ AC1 = √ (CD2 + AD2 + CC12)
Hay AC1 = √ (302 + 402 + 1202) = √ (1302) = 130( cm )
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
