Diện tích hình thoi: Công thức tính và 50 bài tập vận dụng

Hoài Phạm Thị Thu Ngày: 15-11-2024 Tổng hợp kiến thức

Tải xuống 2 2.4 K 11

Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Diện tích hình thoi: Công thức tính và 50 bài tập vận dụng, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Hình thoi , các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Diện tích hình thoi: Công thức tính và 50 bài tập vận dụng

A. Lý thuyết Hình thoi

1. Định nghĩa: Hình thoi là tứ giác có bốn cạnh bằng nhau.

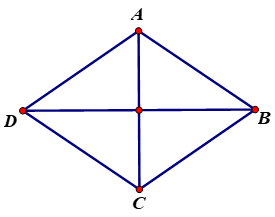
Các dạng bài tập về hình thoi và cách giải

ABCD là hình thoi ⇔ AB = BC = CD = DA.

Nhận xét: Hình thoi cũng là một hình bình hành.

2. Tính chất:

- Hình thoi có tất cả các tính chất của hình bình hành.

- Trong hình thoi:

a) Hai đường chéo vuông góc với nhau;

b) Hai đường chéo là đường phân giác của các góc ở đỉnh của hình thoi.

3. Dấu hiệu nhận biết:

a) Tứ giác có bốn cạnh bằng nhau là hình thoi;

b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi;

c) Hình bình hành có hai đường chéo vuông góc là hình thoi;

d) Hình bình hành có một đường chéo là đường phân giác của một góc ở đỉnh là hình thoi.

4. Diện tích hình thoi

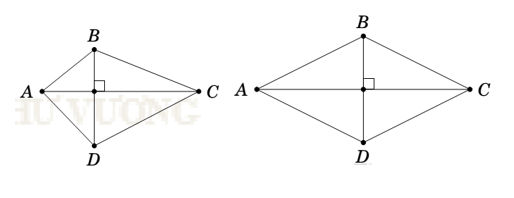
• Diện tích tứ giác ABCD có hai đường chéo vuông góc bằng nửa tích hai đường chéo $S = \frac{1}{2} . A C . B D$ .

• Diện tích hình thoi ABCD bằng nửa tích hai đường chéo $S = \frac{1}{2} . A C . B D$

B. Bài tập Hình thoi

Bài tập trắc nghiệm

Bài 1: Cho hình thoi có độ dài hai đường chéo lần lượt là 8cm, 10cm. Diện tích hình thoi là?

A. 80cm². B. 40cm².

C. 18cm². D. 9cm².

Lời giải:

Diện tích của hình thoi là S = 1/2d₁.d₂

Trong đó d₁,d₂ lần lượt là độ dài hai đường chéo.

Khi đó, diện tích của hình thoi là S_{hình thoi} = 1/2.8.10 = 40( cm² )

Chọn đáp án B.

Bài 2: Hình thoi có độ dài hai đường chéo lần lượt là a√ 2 ,cm, a√ 3 cm. Diện tích của hình thoi là ?

A. a²√ 6 ( cm² )

B. (a²√ 6 )/3( cm² )

C. (a²√ 6 )/2( cm² )

D. (a²√ 5 )/2( cm² )

Lời giải:

Diện tích của hình thoi là S = 1/2d₁.d₂

Trong đó d₁,d₂ lần lượt là độ dài hai đường chéo.

Khi đó, diện tích của hình thoi là S_{hình thoi} = 1/2. a√ 2 . a√ 3 = (a²√ 6 )/2( cm² )

Chọn đáp án C.

Bài 3: Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và BACˆ = 60⁰. Diện tích của hình thoi ABCD là ?

A. 8( cm² ) B. 8√ 3 ( cm² )

C. 16( cm² ) D. 16√ 3 ( cm² )

Lời giải:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Xét hình thoi ABCD có BACˆ = 60⁰.

Ta có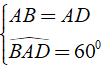 Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án ⇒ Δ ABD đều.

⇒ AB = AD = BD = 4cm

Gọi H là giao điểm của hai đường chéo AC,BD.

Áp dụng định lí Py – to – go ta có:

AH² + HB² = AB² ⇒ AH = √ (AB² - HB²)

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

⇒ AC = 2AH = 4√ 3 ( cm )

Do đó S_ABCD = 1/2AC.BD = 1/2.4√ 3 .4 = 8√ 3 ( cm² )

Chọn đáp án B.

Bài 4: Cho hình thoi ABCD có chu vi bằng 40cm và đường chéo BD = 8cm. Diện tích của hình thoi là ?

A. 16( cm² )

B. 8√ 21 ( cm² )

C. 16√ 21 ( cm² )

D. 8( cm² )

Lời giải:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Gọi H là giao điểm của hai đường chéo AC,BD.

⇒ HB = HD = 4( cm )

Theo giải thiết ta có:

P_ABCD = AB + BC + CD + DA = 40

⇒ AB = BC = CD = DA = 10( cm )

Áp dụng định lý Py – ta – go ta có :

AH² + HB² = AB² ⇒ AH = √ (AB² - HB²) = √ (10² - 4²) = 2√ 21 ( cm )

⇒ AC = 2AH = 4√ 21 ( cm )

Do đó S_ABCD = 1/2.BD.AC = 1/2.4√ (21) .8 = 16√ 21 ( cm² )

Chọn đáp án C.

Bài 5: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Biết OA = 3cm và OB = 5cm. Tính diện tích hình thoi?

A. 30cm² B. 35cm²

C. 40cm² D. 45cm²

Lời giải:

VÌ ABCD là hình thoi nên O là trung điểm của AC và BD

Suy ra: AC = 2OA = 2.3 = 6cm

Và BD = 2.OB = 2.5= 10cm

Diện tích hình thoi là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án A

Bài 6: Cho hình bình hành ABCD có AB = BC = 10 cm và O là giao điểm của hai đường chéo sao cho OA = 6cm. Tính diện tích hình bình hành ABCD

A. 96 B. 80

C. 72 D. 64

Lời giải:

Vì hình bình hành ABCD có 2 cạnh liền kề bằng nhau AB = BC nên ABCD là hình thoi

Suy ra: AB = BC = CD= DA = 10cm và O là trung điểm của AC và trung điểm của BD

Ta có: AC = 2AO = 2. 6 = 12cm

Áp dụng định lí py tago vào tam giác AOD có:

AD² = AO² + OD² suy ra: OD² = AD² – AO² = 10² – 6² = 64 nên OD = 8cm

Suy ra: BD = 2OD = 16cm

Diện tích hình thoi ABCD là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án A

Bài 7: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Diện tích của hình thoi là 120cm²; AC = 12cm . Tính độ dài cạnh của hình thoi

A. 2√30cm B. 2√34cm

C. 8cm D. 9cm

Lời giải:

Diện tích của hình thoi là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.

Suy ra:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Áp dụng định lí Pytago vào tam giác OAB có:

AB² = OA² + OB² = 6² + 10² = 136

⇒ AB = 2√34cm

Chọn đáp án B

Bài 8: Cho hình thoi ABCD có diện tích là 24cm². Tỉ số độ dài hai đường chéo là 3: 4. Tính độ dài hai đường chéo của hình thoi

A. 9cm và 12cm B. 12cm và 16cm

C. 6cm và 8cm D. 3cm và 4cm

Lời giải:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án C

Bài 9: Cho hình thoi ABCD có diện tích là 40cm². Gọi O là giao điểm của hai đường chéo.. Tính diện tích tam giác AOB?

A. 10 cm² B. 12 cm²

C. 8 cm² D. 5 cm²

Lời giải:

Vì ABCD là hình thoi có O là giao điểm của hai đường chéo nên O là trung điểm của AC và BD.

Suy ra

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Diện tích hình thoi ABCD là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Diện tích tam giác vuông OAB là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án A

Bài 10: Cho hình thoi ABCD có O là giao điểm của hai đường chéo biết diện tích tam giác ABC là 16cm². Tính diện tích hình thoi ABCD?

A. 24cm² B. 32cm²

C. 48cm² D. 64cm²

Lời giải:

Do ABCD là hình thoi nên hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường

Diện tích tam giác ABC là

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Suy ra: BO.AC = 32

Diện tích hình thoi ABCD là:

Bài tập Diện tích hình thoi | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án B

Bài tập tự luận

Bài 1. Cho hình thoi có độ dài hai đường chéo là 24 cm và 10 cm. Tính độ dài cạnh hình thoi.

Hướng dẫn giải

Lý thuyết Toán 8 Cánh diều Bài 6: Hình thoi

Giả sử hình thoi có hai đường chéo cắt nhau tại H và AC = 10 cm, BD = 24 cm.

Do ABCD là hình thoi nên:

AC ⊥ BD

$A H = \frac{1}{2} A C = \frac{1}{2} . 10 = 5 (c m)$

$H B = \frac{1}{2} B D = \frac{1}{2} . 24 = 12 (c m)$

Xét tam giác AHB vuông tại H:

AB² = AH² + HB² = 5² + 12² = 169

Do đó AB = 13 cm.

Bài 2. Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Tứ giác AMBM’ là hình gì?

Hướng dẫn giải

Lý thuyết Toán 8 Cánh diều Bài 6: Hình thoi

Vì M’ đối xứng M qua D nên DM = DM’

M là trung điểm BC

D là trung điểm AB

Suy ra MD là đường trung bình của ΔABC.

Suy ra MD // AC.

Mặt khác ΔABC vuông ở A nên AB ⊥ AC.

Do đó AB ⊥ DM hay AB ⊥ MM’.

Vì D là trung điểm của AB và MM’ nên tứ giác AMBM’ là hình bình hành.

Mà AB ⊥ MM’ nên AMBM’ là hình thoi.

Vậy AMBM’ là hình thoi.

Bài 3. Cho hình bình hành ABCD có AC vuông góc với AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD. Chứng minh tứ giác AECF là hình thoi.

Hướng dẫn giải

Lý thuyết Toán 8 Kết nối tri thức Bài 14: Hình thoi và hình vuông

Vì hình bình hành ABCD có AC vuông góc với ADnên $\hat{C A D} = \hat{A C B} = 90 °$ .

Xét tam giác vuông CAD vuông tại A có AF là đường trung tuyến ứng với cạnh huyền CD.

Suy ra $A F = \frac{1}{2} C D \Rightarrow A F = F C = F D = \frac{1}{2} C D$ (1)

Tương tự xét tam giác vuông ACB vuông tại C có CE là đường trung tuyến ứng với cạnh huyền AB.

$\Rightarrow C E = \frac{1}{2} A B \Rightarrow E C = A E = E B = \frac{1}{2} A B$ (2)

Lại có: AB = CD (tính chất hình bình hành) (3)

Từ (1), (2) và (3) suy ra AE = CE = CF = FA

Suy ra tứ giác AECF là hình thoi.

Bài 4. Cho tam giác GHJ cân tại G. Đường trung tuyến kẻ từ G của tam giác cắt HJ tại K. Lấy điểm I trên tia GK sao cho KG = KI. Chứng minh GHIJ là hình thoi.

Hướng dẫn giải

Lý thuyết Toán 8 Chân trời sáng tạo Bài 4: Hình bình hành – Hình thoi

• Ta có GK là trung tuyến của tam giác GHJ nên K là trung điểm của HJ.

Do KG = KI nên K là trung điểm của GI.

Tứ giác GHIJ có hai đường chéo GI và HJ cắt nhau tại trung điểm K của mỗi đường nên là hình bình hành.

• ∆GHJ cân tại G nên đường trung tuyến GK đồng thời là đường cao tương ứng với cạnh HJ nên GI ⊥ HJ.

Hình bình hành GHIJ có hai đường chéo GI và HJ vuông góc với nhau nên là hình thoi

Bài 5. Cho hình thoi ABCD có B là góc tù. Từ B hạ BM ⊥ AD, BN ⊥ CD. Từ D hạ DP ⊥ AB, DQ ⊥ BC. Gọi H là giao điểm của MB và PD, K là giao điểm của BN và DQ, O là giao điểm của AC và BD.

a) Chứng minh H là trực tâm của tam giác ABD.

b) Chứng minh A, H, K, C thẳng hàng.

c) Chứng minh $\hat{P D Q} = \hat{M B N}$ .

d) Chứng minh $\hat{P H M} = \hat{Q K N}$ .

e) Chứng minh tứ giác BHDK là hình thoi.

Hướng dẫn giải

Lý thuyết Toán 8 Chân trời sáng tạo Bài 4: Hình bình hành – Hình thoi

a) Tam giác ABD có hai đường cao BM, DP cắt nhau tại H nên H là trực tâm của tam giác.

b) ABCD là hình thoi nên AC ⊥ BD tại O, do đó A, O, C thẳng hàng (1)

Do H là trực tâm của DABD suy ra AH ⊥ BD tại O nên H ∈ AO (2)

Chứng minh tương tự câu a ta có K là trực tâm DBCD

Suy ra CK ⊥ BD tại O nên K ∈ CO (3)

Từ (1), (2) và (3) suy ra A, H, K, C thẳng hàng.

c) Vì ABCD là hình thoi nên hai đường chéo AC, BD vuông góc với nhau tại trung điểm của mỗi đường

Suy ra AC là đường trung trực của BD

Do đó HB = HD nên DHBD cân tại H, suy ra ${\hat{B}}_{1} = {\hat{D}}_{1}$

Tương tự, ${\hat{B}}_{2} = {\hat{D}}_{2}$

Suy ra ${\hat{B}}_{1} + {\hat{B}}_{2} = {\hat{D}}_{1} + {\hat{D}}_{2}$ hay $\hat{M B N} = \hat{P D Q}$ .

d) ABCD là hình thoi nên $\hat{B A D} = \hat{B C D}$

Tứ giác APHM có $\hat{P H M} = 360 ° - 90 ° - 90 ° - \hat{B A D}$

Tứ giác CQKN có $\hat{Q K N} = 360 ° - 90 ° - 90 ° - \hat{B C D}$

Suy ra $\hat{P H M} = \hat{Q K N}$ .

e) Ta có: ${\hat{A}}_{1} + {\hat{H}}_{2} = 90 °$ và ${\hat{C}}_{1} + {\hat{K}}_{2} = 90 °$

Mà ${\hat{A}}_{1} = {\hat{C}}_{1}$ nên ${\hat{H}}_{2} = {\hat{K}}_{2}$

Lại có ${\hat{H}}_{1} = {\hat{H}}_{2}$ (đối đỉnh) và ${\hat{K}}_{1} = {\hat{K}}_{2}$ (đối đỉnh) nên ${\hat{H}}_{1} = {\hat{K}}_{1}$

Suy ra DBHK cân tại B, nên BH = BK

Mà BH = DH và BK = DK nên BH = HD = CK = KB

Suy ra tứ giác BHDK là hình thoi.

Bài tập tự luyện

Bài 1. Hình thoi ABCD có $\hat{A} = 30 °$ , AB = 4cm. Tính diện tích hình thoi.

Bài 2. Cho hình bình hành ABCD. Lấy M thuộc AB, N thuộc cạnh CD. Gọi P là giao điểm của AN và DM, Q là giao điểm của BN và CM.

a) Chứng minh $S_{Δ A P M} + S_{Δ M B Q} = S_{Δ D N P} + S_{Δ C Q N}$ .

b) Chứng minh $S_{M P N Q} = S_{Δ A D P} + S_{Δ B C Q}$ .

Bài 3. Cho hình thang ABCD (BC là đáy nhỏ). Gọi I là trung điểm của CD. Qua I kẻ đường thẳng d song song với AB. Kẻ AH và BE vuông góc với d. Chứng minh $S_{A B C D} = S_{A B E H}$ .

Bài 4. Trên đường chéo AC của hình vuông ABCD, lấy điểm E (E khác A và C). Qua E kẻ đường thẳng song song với các cạnh và cắt AB, BC, CD, DA lần lượt tại M, N, P, Q. So sánh diện tích MNPQ và diện tích ABCD.

Bài 5. Cho điểm O bất kì nằm trong hình bình hành ABCD. Chứng minh $S_{Δ O A B} + S_{Δ O C D} = S_{Δ O A D} + S_{Δ O B C}$ .

Bài 6. Cho hình thoi ABCD có AB = BD = 6cm.

a) Tính diện tích hình thoi ABCD.

b) Lấy E đối xứng với A qua D. Tính diện tích tứ giác ABCE.

Bài 7. Cho hình vuông ABCD có độ dài cạnh 6cm. Trên AB, CD lần lượt lấy M, N sao cho AM =CN. Tìm vị trí của M để diện tích tứ giác AMCN bằng $\frac{1}{9}$ diện tích tứ giác ABCD.

Tài liệu có 2 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm