Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Tổng hợp công thức tính khoảng cách trong không gian, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Khoảng cách trong không gian, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Tổng hợp công thức tính khoảng cách trong không gian

A. Tổng hợp công thức tính khoảng cách trong không gian

1. Tính khoảng cách hai điểm bất kì

Công thức tính khoảng cách giữa hai điểm cực trị bất kỳ A(xA, yA) và B(xB, yB) như sau:

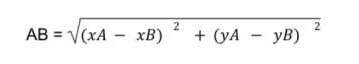2. Tính khoảng cách từ một điểm đến một đường thẳng

+ Cho đường thẳng d: ax + by + c = 0 và điểm M ( x₀; y₀). Khi đó khoảng cách từ điểm M đến đường thẳng d là: d(M; d) = 

+ Cho điểm A( x_A; y_A) và điểm B( x_B; y_B) . Khoảng cách hai điểm này là :

AB = 

3. Tính khoảng cách từ một điểm đến một mặt phẳng

Để tính được khoảng từ điểm A đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm A trên (α)

Cho trước SA ⊥ Δ; trong đó S ∈ (α) và Δ ⊂ (α)

Bước 1: Dựng AK ⊥ Δ ⇒ Δ ⊥ (SAK) ⇒(α) ⊥ (SAK) và (α) ∩ (SAK) = SK

Bước 2: Dựng AP ⊥ SK ⇒ AP ⊥ (α) ⇒ d(A, (α)) = AP

4. Tính khoảng cách hai đường thẳng chéo nhau

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta dựng đoạn vuông góc chung MN của a và b. Khi đó d(a, b) = MN. Sau đây là một số cách dựng đoạn vuông góc chung thường dùng:

Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng $∆$ và song song với $∆$'. Khi đó d($∆$, $∆$') = d($∆$', (α)).

Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

 Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.

- Trường hợp 1:  $∆$ và $∆$' vừa chéo nhau vừa vuông góc với nhau.

Bước 1: Chọn mặt phẳng (α) chứa $∆$' và vuông góc với $∆$ tại I.

Bước 2: Trong mặt phẳng (α) kẻ IJ $\perp$ $∆$'.

Khi đó IJ là đoạn vuông góc chung và d($∆$, $∆$') = IJ.

- Trường hợp 2:  $∆$ và $∆$' vừa chéo nhau và không vuông góc với nhau.

Bước 1: Chọn mặt phẳng (α) chứa $∆$' và song song với $∆$.

Bước 2: Dựng d là hình chiếu vuông góc của $∆$ xuống (α) bằng cách lấy điểm M$\in$ $∆$ dựng đoạn MN $\perp$ (α), lúc đó d là đường thẳng đi qua N và song song với $∆$.

Bước 3: Gọi H = d $\cap$ $∆$', dựng HK // MN.

Khi đó HK là đoạn vuông góc chung và d($∆$, $∆$') = HK = MN.

Hoặc

Bước 1: Chọn mặt phẳng (α)$\perp$ $∆$ tại I.

Bước 2: Tìm hình chiếu d của $∆$' xuống mặt phẳng (α).

Bước 3: Trong mặt phẳng (α), dựng IJ $\perp$ d, từ J dựng đường thẳng song song với $∆$ cắt $∆$' tại H, từ H dựng HM // IJ.

Khi đó HM là đoạn vuông góc chung và d($∆$, $∆$') = HM = IJ.

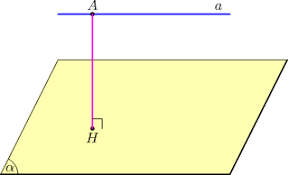
5. Tính khoảng cách giữa đường thẳng và một mặt phẳng song song

Khoảng cách giữa đường thẳng a và mặt phẳng (α) song song với a là khoảng cách từ một điểm bất kì của a tới mặt phẳng (α) cụ thể d(a,(α)) = d (A,(α)) với A thuộc a.

Ta có: d(a, (α)) = d(A, (α)) = AH 

với A thuộc a và H là hình chiếu của A lên mặt phẳng (α).

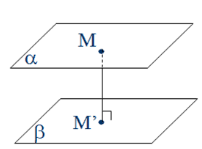
6.Tính khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này tới mặt phẳng kia, cụ thể d((α),(β)) = d(M,(β)) với M thuộc mặt phẳng (α) .

B. Bài tập Khoảng cách trong không gian

Dạng 1: Tính khoảng cách hai điểm bất kì

Bài 1: Trong không gian Oxyz, cho hai điểm A(1;3;-1), B(5;4;-4). Khoảng cách giữa hai điểm A và B là:

Khoảng cách giữa hai điểm A và B là:

$AB=\sqrt{{\left(5-1\right)}^2+{\left(4-3\right)}^2+{\left(-4+1\right)}^2}=\sqrt{26}$

Bài 2: Hãy tính khoảng cách giữa hai điểm A và B trong trường hợp A(2;3;4) và B( 6; 0; 4)

Khoảng cách giữa hai điểm A và B là 

AB = $\sqrt{{(6 - 2)}^{2 }+{(0 - 3)}^{2 }+{(4 - 4)}^2} = 5$

Dạng 2: Tính khoảng cách từ một điểm đến một đường thẳng;

Bài tập vận dụng

Bài 1. Tính khoảng cách từ điểm A(2; 3) đến đường thẳng d: 5x – 3y – 2 = 0.

Hướng dẫn giải:

Khoảng cách từ điểm A(2; 3) đến đường thẳng d: 5x – 3y – 2 = 0 là:

d(A; d) = $\frac{\left|5.2-3.3-2\right|}{\sqrt{5^2+{\left(-3\right)}^2}}=\frac{\sqrt{34}}{34}$.

Bài 2. Tính khoảng cách từ điểm O đến đường thẳng d: 3x + 2y – 1 = 0.

Hướng dẫn giải:

Khoảng cách từ điểm O đến đường thẳng d: 3x + 2y – 1 = 0 là:

d(O; d) = $\frac{\left|5.0+2.0-1\right|}{\sqrt{5^2+2^2}}=\frac{\sqrt{29}}{29}$.

Bài 3. Tính khoảng cách từ điểm A(–5; 2) đến đường thẳng d: 2x –y + 5 = 0.

Hướng dẫn giải:

Khoảng cách từ điểm A(–5; 2) đến đường thẳng d: 2x –y + 5 = 0 là:

d(A; d) = $\frac{\left|2.\left(-5\right)-1.2+5\right|}{\sqrt{2^2+{\left(-1\right)}^2}}=\frac{7\sqrt{5}}{5}$.

Bài 4. Tính khoảng cách từ điểm O đến đường thẳng d: $\frac{x}{3}+\frac{y}{2}=5$.

Hướng dẫn giải:

Đường thẳng d: $\frac{x}{3}+\frac{y}{2}=5\iff \frac{x}{3}+\frac{y}{2}-5=0$

Khoảng cách từ điểm O đến đường thẳng d: $\frac{x}{3}+\frac{y}{2}=5$ là:

d(O; d) = $\frac{\left|\frac{0}{3}+\frac{0}{2}-5\right|}{\sqrt{{\left(\frac{1}{3}\right)}^2+{\left(\frac{1}{2}\right)}^2}}=\frac{30\sqrt{13}}{13}$.

Bài 5. Tính khoảng cách từ điểm B(3; –5) đến đường thẳng {x = 2 + 3t; y = 5 – 2t}.

Hướng dẫn giải:

Xét đường thẳng d: {x = 2 + 3t; y = 5 – 2t}

2x + 3y = 2(2 + 3t) + 3(5 – 2t) = 4 + 6t + 15 – 6t = 19

Do đó 2x + 3y - 19 = 0

Khoảng cách từ điểm B(3; –5) đến đường thẳng d: 2x + 3y – 19 = 0 là:

d(B; d) = $\frac{\left|2.3+3.\left(-5\right)-19\right|}{\sqrt{2^2+3^2}}=\frac{28\sqrt{13}}{13}$.

Bài tập tự luyện

Bài 1. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Tính Bán kính R của đường tròn (C).

Bài 2.  Tính Khoảng cách từ giao điểm của hai đường thẳng a: x - 3y + 4 = 0 và b: 2x + 3y - 1 = 0 đến đường thẳng d: 3x + y + 16 = 0.

Bài 3. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (d₁): 2x – 3y + 6 = 0 và (d₂): 5x + 3y – 2 = 0, đỉnh A(3; 5). Tính diện tích của hình chữ nhật.

Bài 4. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a): 3x – 2y + 1 = 0 và (b): 4x + 3y – 3 = 0. Biết hình chữ nhật có đỉnh là giao điểm của hai đường thẳng a: 2x – 3y + 2 = 0 và b: 4x + 3y – 3 = 0. Tính diện tích của hình chữ nhật.

Bài 5. Đường tròn (C) có tâm I (–2; –2) và tiếp xúc với đường thẳng d: 5x + 12y – 10 = 0. Tính bán kính R của đường tròn (C).

Dạng 3: Tính khoảng cách từ một điểm đến một mặt phẳng

Bài tập vận dụng

Câu 1: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến (BCD) bằng:

Lời giải:

Chọn B

Gọi O là trọng tâm tam giác BCD

⇒ OB = OC = OD (do tam giác BCD là tam giác đều)

Lại có: AB = AC = AD = a

⇒ AO là trục đường tròn ngoại tiếp tam giác BCD

⇒ AO ⊥ (BCD)

Câu 2: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Khoảng cách từ O đến mặt phẳng (SBC) là:

Lời giải:

Chọn C

+ Trong mặt phẳng ( ABCD), kẻ OK ⊥ BC (K ∈ BC)

+ Mà BC ⊥ SO nên suy ra hai mặt phẳng (SOK) và (SBC) vuông góc nhau theo giao tuyến SK.

+ Trong mặt phẳng (SOK), kẻ OH ⊥ SK (H ∈ SK)

Suy ra: OH ⊥ (SBC) ⇒ d(O, (SBC)) = OH

+ Xét mp(ABCD) có:

+ xét tam giác SOK vuông tại O ta có:

Câu 3: Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60°; tam giác ABC cân tại C, tam giác ABD cân ở D. Đường cao DM của tam giác ABD bằng 12 cm. Khoảng cách từ D đến (ABC) bằng

A. 3√3 cm              B. 6√3 cm              C. 6 cm              D. 6√2 cm

Lời giải:

+ Gọi M là trung điểm AB.

Do tam giác ABC cân tại C và tam giác ABD cân tại D nên CM ⊥ AB; DM ⊥ AB suy ra: AB ⊥ (CDM)

+ Do hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60° nên ∠CMD = 60°

+ Gọi H là hình chiếu vuông góc của D lên CM

⇒ DH = d(D, (ABC))

Xét tam giác DHM có:

DH = DM.Sin 60° = 6√3

Chọn đáp án B

Câu 4: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Khoảng cách từ A đến (B’CD’) bằng

Lời giải:

Ta có: AB’ = AC = AD’ = B’D’ = B’C = CD’ = a√2

⇒ Tứ diện AB’CD’ là tứ diện đều.

Gọi I là trung điểm B’C và G là trọng tâm tam giác B’CD’.

Ta có : AC = AD’ = AB’ và GB’ = GC = GD’

nên AG ⊥ (B'CD')

Khi đó ta có: d(A , (B’CD’)) = AG

Vì tam giác B’CD’ đều cạnh a√2 nên 

Theo tính chất trọng tâm ta có: 

Trong tam giác vuông AGD’ có:

Chọn C

Câu 5: Cho hình chóp S. ABC có đáy ABC là tam giác vuông cân tại A với AB = a. Mặt bên chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc 45°. Tính khoảng cách từ điểm S đến mặt phẳng đáy (ABC) .

Lời giải:

Gọi H là hình chiếu của S lên (ABC) , vì mặt bên (SBC) vuông góc với (ABC) nên H ∈ BC

Dựng HI ⊥ AB, HJ ⊥ AC, theo đề bài ta có ∠SIH = ∠SJH = 45°.

Do đó: ΔSHI = ΔSHJ (cạnh góc vuông - góc nhọn)

Suy ra : HI = HJ

Lại có ∠B = ∠C = 45° ⇒ ΔBIH = ΔCJH ⇒ HB = HC

Vậy H trùng với trung điểm của BC

Từ đó ta có HI là đường trung bình của tam giác ABC nên HI = AC/2 = a/2

Tam giác SHI vuông tại H và có ∠SIH = 45° ⇒ ΔSHI vuông cân.

Do đó: SH = HI = a/2

Chọn đáp án A

Câu 6: Cho hình chóp tam giác đều S.ABC có cạnh bên bằng b cạnh đáy bằng d, với d < b√3. Hãy chọn khẳng định đúng trong các khẳng định bên dưới.

Lời giải:

Gọi I là trung điểm của BC và H là trọng tâm tam giác ABC.

Do S.ABC là hình chóp đều nên SH ⊥ (ABC) ⇒ d(S, (ABC)) = SH

Chọn C

Câu 7: Cho hình lập phương ABCD. A₁B₁C₁D₁ cạnh bằng a. Gọi M là trung điểm của AD. Khoảng cách từ A₁ đến mặt phẳng (C₁D₁M) bằng bao nhiêu?

Lời giải:

Gọi N là trung điểm cạnh DD₁ và

Ta có: ΔA₁ND₁ = ΔD₁MD    (c.g.c)

Chọn đáp án A

Câu 8: Cho hình chóp tam giác đều S. ABC có cạnh đáy bằng 3a cạnh bên bằng 2a. Khoảng cách từ S đến mặt phẳng (ABC) bằng:

A. 4a              B. 3a              C. a              D. 2a

Lời giải:

Gọi G là trọng tâm tam giác ABC

Do S.ABC là hình chóp đều nên SG ⊥ (ABC)

Tam giác SAG vuông tại G có:

Chọn đáp án C

Câu 9: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng a√2. Tính khoảng cách từ tâm O của đáy ABCD đến một mặt bên:

Lời giải:

Chọn B

Gọi O là tâm của hình vuông ABCD và M là trung điểm của CD

Do hình chóp S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD)

Kẻ OH ⊥ SM, ta có:

Câu 10: Cho hình chóp S.ABCD có mặt đáy là hình thoi tâm O, cạnh a và góc ∠BAD = 120°, đường cao SO = a. Tính khoảng cách từ điểm O đến mặt phẳng (SBC).

Lời giải:

Vì hình thoi ABCD có ∠BAD bằng 120° nên ∠ABC = 60°

⇒ tam giác ABC đều cạnh a.

Kẻ đường cao AM của tam giác ABC ⇒ AM = a√3/2

Kẻ OI ⊥ BC tại I ⇒ OI = AM/2 = a√3/4 .

Kẻ OH ⊥ SI ⇒ OH ⊥ (SBC)

⇒ d(O; (SBC)) = OH

Xét tam giác vuông SOI ta có:

Chọn D

Câu 11: Cho hình chóp S.ABCD có mặt đáy ABCD là hình thoi cạnh a, ∠ABC = 120°. Hình chiếu vuông góc của đỉnh S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD, ∠ASC = 90°. Khoảng cách từ điểm A đến mặt phẳng (SBD) tính theo a bằng

Lời giải:

Xác định khoảng cách:

- Ta có đáy ABCD là hình thoi, góc ∠ABC = 120° nên ∠ABD = 60° và tam giác ABD đều cạnh a

Ta có: AC = a√3, AG = a√3/3

Tam giác SAC vuông ở S, có đường cao SG nên

Xét hình chóp S. ABD có chân đường cao trùng với tâm của đáy nên SA = SB = SD = a.

- Dựng hình chiếu của A lên mặt phẳng (SBD): Kẻ đường cao AH của tam giác SAO với O là tâm của hình thoi.

AH = a√6/3

Cách khác: Nhận xét tứ diện S.ABD có tất cả các cạnh bằng a. Do đó S.ABD là tứ diện đều, vậy AH = SG = a√6/3

Chọn đáp án D

Câu 12: Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a; AC = 2a và SA vuông góc với mặt phẳng (ABCD); SC tạo với mặt phẳng (SAB) một góc 30°. Gọi M là một điểm trên cạnh AB sao cho BM = 3MA. Khoảng cách từ điểm A đến mặt phẳng (SCM)?

Lời giải:

+ Ta có: 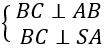 nên BC ⊥ (SAB)

Khi đó; SC tạo với mặt phẳng (SAB) góc 30° nên ∠CSB = 30°

+ Xác định khoảng cách: d(A; (SBC)) = AH

Tính AH:

Chọn đáp án B

Câu 13: Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác vuông tại S hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AD sao cho HA = 3 HD. Gọi M là trung điểm của cạnh AB. Biết rằng SA = 2√3.a và đường thẳng SC tạo với mặt đáy một góc 30°. Khoảng cách từ M đến mặt phẳng (SBC) tính theo a bằng

Lời giải:

+ SC có hình chiếu vuông góc lên mp(ABCD) là HC ⇒ (SC, (ABCD)) = ∠SCH = 30°

Đặt AD = 4x (x > 0)

Xét tam giác SAD vuông tại S ta có:

Chọn D

Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi I là trung điểm của cạnh AB. Hình chiếu vuông góc của đỉnh S lên mặt phẳng đáy là trung điểm H của CI góc giữa đường thẳng SA và mặt đáy bằng 60°. Khoảng cách từ điểm H đến mặt phẳng (SAC) là

Lời giải:

Chọn A

+ Do góc giữa SA và mp(ABC) là 60° nên ∠SAH = 60°

+ Ta có; CI = CA.sin60° = (a√3)/2; AI = AB/2 = a/2

Trong tam giác ACI có trung tuyến AH suy ra

Trong tam giác SHA vuông tại H và ∠SAH = 60° suy ra SH = AH √3 = a√21/4

Gọi E; F lần lượt là hình chiếu của H trên AC và SE. Khi đó d(H; (SAC)) = HF

Ta có:

 

Bài tập tự luyện

Bài 1. Cho hình chóp S.ABC có đáy là tam giác vuông tại A, biết SA ⊥ (ABC) và AB = 2a; AC = 3a; SA = 4a. Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).

Bài 2. Cho hình chóp S.ABC có SA = 3a, SA vuông góc (ABC), AB = 2a, $\widehat{ABC}=120°$. Tính khoảng cách từ A đến mặt phẳng (SBC).

Bài 3. Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên tia Ax vuông góc với mặt phẳng (P) lấy điểm S sao cho SA = a. Tính khoảng cách từ A đến (SBC).

Bài 4. Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B, AB = a, SA vuông góc với mặt phẳng đáy và SA = 2a. Tính khoảng cách từ A đến mặt phẳng (SBC).

Bài 5. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, ABC là tam giác vuông đỉnh B có AB = a. Biết SA = 2a. Tính khoảng cách từ A đến (SBC).

Bài 6. Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ A đến (BCD)?

Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC = 60. Mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy. Trên cạnh SC lấy điểm M sao cho MC = 2MS. Khoảng cách từ điểm M đến mặt phẳng (SAB) bằng?

Bài 8. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD = 2AB = 2BC, CD = $2a\sqrt{2}$. Hình chiếu vuông góc của S trên mặt đáy là trung điểm M của cạnh CD. Khoảng cách từ điểm B đến mặt phẳng (SAM) bằng?

Bài 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành với BC = $a\sqrt{2}$, $\widehat{ABC}=60°$. Cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ điểm D đến mặt phẳng (SAB) bằng?

Bài 10. Cho khối chóp S.ABCD có đáy là hình chữ nhật ABCD với AB = a. Hình chiếu vuông góc của đỉnh S lên mặt đáy trùng với trọng tâm của tam giác ABD. Biết SC = $2a\sqrt{2}$ và tạo với đáy một góc 45°. Khoảng cách từ trung điểm của SD đến mặt phẳng (SAC) bằng bao nhiêu?

Bài 11. Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng các giữa hai đường thẳng AB và CD.

Bài 12. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA vuông góc với mặt đáy SA = a. Tính:

a) Khoảng cách từ điểm S đến mp(A1CD) trong đó A1 là trung điểm của SA;

b) Khoảng cách giữa AC và SD.

Bài 13. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng $a\sqrt{2}$

a. Tính khoảng cách từ S đến mp(ABCD).

b. Tính khoảng cách giữa đường thẳng AB và mp(SCD).

c. Tính khoảng cách giữa hai đường thẳng AB và SC.

d. Gọi P là mặt phẳng đi qua A và vuông góc với SC. Hãy xác định thiết diện của hình chóp khi cắt bởi (P). Tính diện tích thiết diện.

e. Tính góc giữa đường thẳng AB và mp(P).

Bài 14. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Mặt bên SAB là tam giác cân tại S và mp(SAB) vuông góc với mp(ABCD), cạnh SC tạo với mặt phẳng đáy góc α. Tính:

a) Chiều cao của hình chóp S.ABCD;

b) Khoảng cách từ chân đường cao hình chóp đến mặt phẳng (SCD);

c) Diện tích thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng trung trực của cạnh BC.

Bài 15. Cho hình chóp tứ giác đều .SABCD có đáy bằng 2a , SA tạo với đáy một góc 30°. Tính theo a khoảng cách d giữa hai đường thẳng SA và CD.

Dạng 4: Tính khoảng cách hai đường thẳng chéo nhau

Bài tập vận dụng

Ví dụ 1. Cho hình chóp S.ABCD có đáy hình vuông ABCD tâm O cạnh $a\sqrt{2}$ , cạnh $SA=a\sqrt{2}$  và vuông góc mặt đáy.

a) Tính khoảng cách giữa BC và SD.

b) Tính khoảng cách giữa SC và AD.

Hướng dẫn giải:

a) Vì SA $\perp$ (ABCD) $\Rightarrow$ SA $\perp$ CD.

Do ABCD là hình vuông nên CD $\perp$ AD.

Ta có: CD $\perp$ SD tại D, CD $\perp$ BC tại C.

$\Rightarrow$ CD là đoạn vuông góc chung của SD và BC.

$\Rightarrow$ d(SD, BC) = CD = 2a.

b) Vì AD // BC mà BC$\subset$ (SBC) $\Rightarrow$ AD // (SBC).

Do đó d(AD, SC) = d(AD, (SBC)) = d(A, (SBC)).

Kẻ AH $\perp$ SB tại H.

Có SA$\perp$ (ABCD) $\Rightarrow$ SA $\perp$BC mà BC $\perp$ AB $\Rightarrow$ BC $\perp$(SAB) $\Rightarrow$ BC $\perp$AH.

Lại có AH $\perp$ SB nên AH $\perp$ (SBC).

Do đó d(A, (SBC)) = AH.

Xét $∆$SAB vuông tại A, có $\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{B}^2}=\frac{1}{2a^2}+\frac{1}{2a^2}=\frac{1}{a^2}\Rightarrow AH=a$.

Vậy d(SC, AD) = a.

Ví dụ 2. Cho lăng trụ đứng ABCD.A'B'C'D' có tất cả các cạnh bằng a, góc $\widehat{DAB}=120°$ .

a) Tính khoảng cách giữa BD và CC'.

b) Tính khoảng cách giữa AC và BD'.

Hướng dẫn giải:

a) Gọi O là tâm của hình thoi ABCD.

Vì ABCD là hình thoi nên O là trung điểm của AC, BD và AC $\perp$ BD.

Xét DABD có BD² = AB² + AD² – 2AB.AD.cos120° = 3a²

$\Rightarrow$ $BD=a\sqrt{3}\Rightarrow BO=\frac{a\sqrt{3}}{2}$

Xét DAOB vuông tại O, có $AO=\sqrt{A{B}^2-B{O}^2}=\sqrt{a^2-\frac{3a^2}{4}}=\frac{a}{2}$  $\Rightarrow$ AC = a.

Vì CC' $\perp$ (ABCD) $\Rightarrow$ CC' $\perp$ CO mà CO$\perp$ BD nên CO là đoạn vuông góc chung của BD và CC'.

Do đó d(BD, CC') = CO = AO = $\frac{a}{2}$ .

b) Trong (BDD'B') kẻ OE $\perp$ BD' tại E (1).

Vì AC $\perp$ BD và AC $\perp$ DD' (DD' $\perp$ (ABCD)) $\Rightarrow$ AC $\perp$ (BDD'B')$\Rightarrow$ AC $\perp$OE (2).

Từ (1) và (2), suy ra OE là đoạn vuông góc chung của AC và BD'.

Do đó d(AC, BD') = OE.

Mà OE = d(O, BD') = $\frac{1}{2}d\left(D,B{D}^{\text{'}}\right)$.

Gọi h là khoảng cách từ D đến BD'.

Xét DD'DB vuông tại D, có $\frac{1}{h^2}=\frac{1}{D{D^{\text{'}}}^2}+\frac{1}{D{B}^2}=\frac{1}{a^2}+\frac{1}{3a^2}=\frac{4}{3a^2}\Rightarrow h=\frac{a\sqrt{3}}{2}$ .

Vậy d(AC, BD') = $\frac{a\sqrt{3}}{4}$ .

Bài tập tự luyện

Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy ABCD. Gọi K, H theo thứ tự là hình chiếu vuông góc của A và O lên SD. Chọn khẳng định đúng trong các khẳng định sau?

A.Đoạn vuông góc chung của AC và SD là AK;

B.Đoạn vuông góc chung của AC và SD là CD;

C.Đoạn vuông góc chung của AC và SD là OH;

D.Các khẳng định trên đều sai.

Bài 2. Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.

A. $\frac{a\sqrt{3}}{2}$ ;

B. $\frac{a\sqrt{2}}{3}$;

C. $\frac{a\sqrt{2}}{2}$;

D. $\frac{a\sqrt{3}}{3}$.

Bài 3. Cho hình chóp S.ABCD có SA $\perp$ (ABCD), đáy ABCD là hình chữ nhật với $AC=a\sqrt{5}$ và $BC=a\sqrt{2}$ . Tính khoảng cách giữa SD và BC.

A. $\frac{3a}{4}$ ;

B. $\frac{2a}{3}$;

C. $\frac{a\sqrt{3}}{2}$;

D. $a\sqrt{3}$.

Bài 4. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa BB' và AC bằng:

A. $\frac{a}{2}$ ;

B. $\frac{a}{3}$;

C. $\frac{a\sqrt{2}}{2}$;

D. $\frac{a\sqrt{3}}{3}$.

Bài 5. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1. Khoảng cách giữa AA' và BD' bằng:

A. $\frac{\sqrt{3}}{3}$ ;

B. $\frac{\sqrt{2}}{2}$ ;

C. $\frac{2\sqrt{2}}{5}$;

D. $\frac{3\sqrt{5}}{7}$.

Bài 6. Cho khối lập phương ABCD.A'B'C'D'. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A'C' là:

A. AA';

B. BD;

C. DA';

D. DD'.

Bài 7. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD nhận giá trị nào trong các giá trị sau?

A. a;

B. $a\sqrt{2}$ ;

C. $a\sqrt{3}$ ;

D. 2a.

Bài 8. Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc với nhau, OA = OB = OC = a. Gọi I là trung điểm BC. Khoảng cách giữa AI và OC bằng bao nhiêu?

A. a;

B. $\frac{a}{\sqrt{5}}$ ;

C. $\frac{a\sqrt{3}}{2}$ ;

D. $\frac{a}{2}$ .

Bài 9. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a, SA vuông góc với mặt đáy và SA = a. Tính khoảng cách giữa SB và CD.

A. $\frac{a\sqrt{2}}{4}$ ;

B. $\frac{a}{2}$ ;

C. $\frac{a\sqrt{3}}{3}$ ;

D. $\frac{a\sqrt{2}}{2}$ .

Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h.  Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BD.

A. $\frac{ah}{\sqrt{3a^2+h^2}}$ ;

B. $\frac{ah}{\sqrt{a^2+h^2}}$ ;

C. $\frac{ah}{\sqrt{2a^2+h^2}}$ ;

D. $\frac{ah}{\sqrt{a^2+2h^2}}$ .

Dạng 5: Tính khoảng cách giữa đường thẳng và một mặt phẳng song song

Bài tập vận dụng

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = a√2. Gọi E là trung điểm AD. Khoảng cách giữa AB và (SOE) là

Lời giải:

+ Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy .

mà (SAB) ∩ (SAD) = SA

⇒ SA ⊥ (ABCD) .

+ Do E là trung điểm của AD khi đó

Tam giác ABD có EO là đường trung bình

⇒ EO // AB ⇒ AB // (SOE)

⇒ d(AB, (SOE)) = d(A; (SOE)) = AH

với H là hình chiếu của A lên SE.

Câu 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 (đvdt). Khoảng cách giữa AA’ và (BB’D’) bằng:

Lời giải:

Chọn B

Ta có: AA’ // BB’ mà BB’ ⊂ ( BDD’B’)

⇒ AA’ // (BDD’B’)

⇒ d( AA’; (BD’B’)) = d(A; (BDD’B’)

Gọi O là giao điểm của AC và BD

⇒ AO ⊥ (BDD’B’) (tính chất hình lập phương)

Câu 3: Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật với AC = a√5 và BC = a√2. Tính khoảng cách giữa (SDA) và BC?

Lời giải:

+ Ta có: BC // AD nên BC // (SAD)

⇒ d(BC; (SAD)) = d(B; SAD))

+ Ta chứng minh BA ⊥ (SAD) :

Do BA ⊥ AD (vì ABCD là hình chữ nhật)

Và BA ⊥ SA (vì SA ⊥ (ABCD))

⇒ BA ⊥ (SAD)

⇒ d(B; (SAD)) = BA

Áp dụng định lí Pytago trong tam giác vuông ABC có:

AB² = AC² - BC² = 5a² - 2a² = 3a²

⇒ AB = √3 a

⇒ d(CB; (SAD)) = AB = √3 a

Đáp án D

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AB = 2a; BC = a . Các cạnh bên của hình chóp bằng nhau và bằng a√2 . Gọi E và F lần lượt là trung điểm của AB và CD; K là điểm bất kỳ trên BC. Khoảng cách giữa hai đường thẳng EF và (SBK) là:

Lời giải:

Gọi O là giao điểm của AC và BD; I là trung điểm cạnh BC

+ Do SA = SB = SC = SD và OA = OB = OC = OD nên SO ⊥ (ABCD)

+ Ta chứng minh BC ⊥ (SOI)

- Tam giác SBC cân tại S có SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI    (1).

- Lại có: BC ⊥ SO (vì SO ⊥ (ABCD))    (2)

Từ ( 1) và ( 2) suy ra: BC ⊥ (SOI)

Mà OH ⊂ (SOI) nên BC ⊥ OH

⇒ OH ⊥ (SBC)

Do EF // BK nên EF // (SBK)

⇒ d(EF; (SBK)) = d(O; (SBK)) = OH

Chọn đáp án D.

Câu 5: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B; AB= a cạnh bên SA vuông góc với đáy và SA = a√2. Gọi M và N lần lượt là trung điểm của AB; AC. Khoảng cách giữa BC và (SMN) bằng bao nhiêu?

Lời giải:

+ Tam giác ABC có MN là đường trung bình nên MN // BC

⇒ BC // (SMN) nên :

d(BC; (SMN)) = d(B; (SMN)) = d(A; (SMN))

Gọi H là hình chiếu vuông góc của A trên đoạn SM.

+ Ta chứng minh: MN ⊥ (SAM):

Chọn đáp án A

Câu 6: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên SA = SB = SC = SD = a√2. Khoảng cách giữa hai đường thẳng AD và (SBC) là:

Lời giải:

+ Do AD // BC nên AD // (SBC)

⇒ d (AD, (SBC)) = d(H; (SBC))

trong đó H là trung điểm AD.

+ Gọi M là trung điểm của BC và K là hình chiếu vuông góc của H lên SM

⇒ d(H; (SBC)) = HK.

+ Diện tích tam giác SMH là:

Chọn đáp án C

Câu 7: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SD = a√17/2 . Hình chiếu vuông góc H của đỉnh S lên mặt phẳng (ABCD) là trung điểm của cạnh AB. Gọi K là trung điểm của AD. Tính khoảng cách giữa hai đường HK và (SBD) theo a

Lời giải:

+ Ta có: H và K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ABD

⇒ HK // BD ⇒ HK // (SBD)

⇒ d(HK; (SBD)) = d(H, (SBD))

Kẻ HI ⊥ BD và HJ ⊥ SI

Chọn đáp án C

Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ∠ABC = 60° Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 30°. Khoảng cách giữa hai đường thẳng CD và (SAB) theo a bằng:

Lời giải:

Gọi O là giao điểm của AC và BD

Kẻ: OI ⊥ AB; OH ⊥ SI

+ Do CD // AB nên CD // (SAB)

⇒ d(CD, (SAB)) = d(C; (SAB)) = 2d( O; (SAB))

Ta có: AB ⊥ SO , AB ⊥ OI ⇒ AB ⊥ (SOI) ⇒ AB ⊥ OH

Nên OH ⊥ (SAB) ⇒ d(O, (SAB)) = OH

Mà tam giác ACB cân tại B có ∠ABC = 60° nên tam giác ABC đều

⇒ OC = (1/2)AC = (1/2)AB = a/2 .

+ xét tam giác OAB có:

Chọn đáp án B

Câu 9: Cho hình chóp tứ giác đều S.ABCD có đường cao SO = 2, mặt bên hợp với mặt đáy một góc 60°. Khi đó khoảng cách giữa hai đường thẳng AB và (SCD) bằng

Lời giải:

+ Gọi I là trung điểm của CD . Ta có:

⇒ ((SCD), (ABCD)) = (OI, SI) = 60°

+ Ta có: AB // CD nên AB // (SCD)

⇒ d(AB, (SCD)) = d(A, ( SCD)) = 2.d(O, (SCD))

+ Trong mp (SOI) , gọi H là hình chiếu vuông góc của O lên SI

+ Tam giác SOI vuông tại O, có đường cao OH nên

Do đó: d(AB; (SCD)) = 2d(O; (SCD)) = 2.OH = 2.1 = 2

Chọn B

Bài tập tự luyện

Bài 1. Cho hình thang vuông ABCD vuông ở A và D; AD = a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với SD = $a\sqrt{3}$. Tính khỏang cách giữa đường thẳng CD và (SAB).

Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Biết hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy và SA = $a\sqrt{2}$. Gọi E là trung điểm AD. Khoảng cách giữa AB và (SOE) bằng bao nhiêu?

Bài 3. Cho hình chóp S.ABCD có SA ⊥ (ABCD) đáy ABCD là hình chữ nhật với AC = $a\sqrt{5}$ và BC = $a\sqrt{2}$. Tính khoảng cách giữa (SDA) và BC.

Bài 4. Cho hình chóp tứ giác đều S.ABCD có đường cao SO = 2, mặt bên hợp với mặt đáy một góc 60°. Tính khoảng cách giữa hai đường thẳng AB và (SCD).

Bài 5. Cho hình chóp tứ giác đều S.ABCD có AB = SA = a . Khoảng cách từ đường thẳng AB đến (SCD) bằng bao nhiêu?

Dạng 6: Tính khoảng cách giữa hai mặt phẳng song song

Bài tập vận dụng 

Câu 1: Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC và A’D’. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC’)

Lời giải:

Nhận xét (ACC') ≡ (ACC'A')

Gọi O = AC ∩ BD, I = MN ∩ BD

+ Ta có M và N lần lượt là trung điểm của AD và DC nên MN là đường trung bình của tam giác ADC và MN // AC    (1)

+ Tương tự: M, P lần lượt là trung điểm của AD và A’D’ nên MP là đường trung bình của hình thang A’D’DA

⇒ MP // AA’ // PP’    (2) .

Từ (1) và (2) suy ra: (MNP) // (ACC’)

Mà O thuộc mp( ACC’) nên d((MNP); (ACC’) ) = d(O; (ACC’))

+ Ta có: OI ⊥ AC và OI ⊥ AA’ (vì AA’ ⊥ (ABCD) và OI ⊂ (ABCD))

⇒ OI ⊥ (ACC’A’) nên d(O; (ACC’)) = OI

Suy ra 

Chọn đáp án B

Câu 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó, khoảng cách giữa hai mặt phẳng (CB’D’) và (BDA’) bằng

Lời giải:

+ Ta có: BD // B’D’ và A’D // B’C

⇒ (A'BD) // (B'CD') nên ta có:

d((A’BD); (CB’D’)) = d(B’; (A’BD)) = d(A; (A’BD))

+ Vì AB = AD = AA’ = a và A'B = A'D = BD = a√2

⇒ Hình chóp A.A’BD là hình chóp tam giác đều.

+ Gọi I là trung điểm A’B và G là trọng tâm tam giác A’BD.

⇒ AG ⊥ (A’BD)

Khi đó ta có: d(A ; (A’BD)) = AG

+ Vì tam giác A’BD đều cạnh a√2 nên

Theo tính chất trọng tâm ta có:

Trong tam giác vuông AGD có:

Chọn B

Câu 3: Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khoảng cách giữa (ACB’) và (DA’C’) bằng

Lời giải:

+ Ta có : AC // A’C’ và B’C // A’D

=> (ACB') // (DA'C')

Lại có: D ∈ mp(DA'C') nên d((ACB'), (DA'C')) = d(D, (ACB')) = d(B, (ACB'))

+ Vì BA = BB’ = BC = a và nên hình chóp B.ACB’ là hình chóp tam giác đều

+ Gọi I là trung điểm AC và G là trọng tâm tam giác ACB’.

⇒ BG ⊥ (ACB’)

Khi đó ta có: d(B, (ACB')) = BG

+ Vì tam giác ACB’ đều cạnh a√2 nên 

Theo tính chất trọng tâm ta có: 

Trong tam giác vuông BGB’ có:

Chọn C

Câu 4: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 4; AD = 3. Mặt phẳng (ACD’) tạo với mặt đáy một góc 60°. Tính khoảng cách giữa hai mặt đáy của hình hộp.

Lời giải:

+ Gọi O là hình chiếu của D lên AC.

+ Khoảng cách giữa hai mặt đáy là:

Chọn đáp án B

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi M, N và P lần lượt là trung điểm của các cạnh AB, AD và DC. Gọi J là trung điểm SA và H là giao điểm của CN và DM, biết SH vuông góc (ABCD), SH = a√3. Khoảng cách từ (MDJ) đến mặt phẳng (SBP) tính theo a bằng

Lời giải:

+ Ta có: MJ // SB (vì MJ là đường trung bình của tam giác SAB). Và MD // BP

⇒ (DMJ) //( SBP)

⇒ d((DMJ); (SBP)) = d(H, (SBP)).

+ Ta chứng minh: NC ⊥ MD

Chọn C

Bài tập tự luyện

Bài 1. Cho hình lăng trụ tứ giác đều ABCD.A′B′C′D′ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC, A'D'. Tính khoảng cách giữa hai mặt phẳng (MNP) và (ACC').

Bài 2. Cho hình lăng trụ tam giác ABC.A₁B₁C₁ có cạnh bên bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc 60°. Hình chiếu vuông góc của A lên mặt phẳng (A₁B₁C₁) là trung điểm của B₁C₁. Khoảng cách giữa hai mặt đáy của lăng trụ bằng bao nhiêu?

Bài 3. Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Tính khoảng cách giữa hai mặt phẳng (BA′C′) và (ACD′).

Bài 4. Cho hình lăng trụ ABC.AB’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30°. Hình chiếu H của A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’. Khoảng cách giữa hai mặt phẳng đáy là?

Bài 5. Cho hình lập phương ABCD.A'B'C'D; cạnh a. Khoảng cách giữa (AB’C) và (A’DC’) bằng?