Khoảng cách từ 1 điểm đến đường thẳng là gì? Công thức tính và bài tập

Quang Trung Ngày: 08-03-2024 Tổng hợp kiến thức

Tải xuống 18 3.1 K 18

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Khoảng cách từ 1 điểm đến đường thẳng, tài liệu bao gồm có định nghĩa, các tính khoảng cách từ một điểm đến một đường thẳng và các bài tập vận dụng. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Khoảng cách từ 1 điểm đến đường thẳng

1. Định nghĩa

- Khoảng cách từ điểm $M$ đến đường thẳng $Δ$ là khoảng cách giữa hai điểm $M$ và $H$ , trong đó $H$ là hình chiếu của điểm $M$ trên đường thẳng $Δ$ .

Kí hiệu: $d (M, Δ) = M H$ trong đó $H$ là hình chiếu của $M$ trên $Δ$ .

2. Bài toán tính khoảng cách từ một điểm đến một đường thẳng

Phương pháp 1:

Để tính khoảng cách từ điểm $M$ đến đường thẳng $Δ$ ta cần xác định được hình chiếu $H$ của điểm $M$ trên đường thẳng $Δ$ , rồi xem $M H$ là đường cao của một tam giác nào đó để tính.

Điểm $H$ thường được dựng theo hai cách sau:

Cách 1: Trong $m p (M, Δ)$ vẽ $M H ⊥ Δ \Rightarrow d (M, Δ) = M H$

Cách 2: Dựng mặt phẳng $(α)$ qua $M$ và vuông góc với $Δ$ tại $H$ .

Khi đó $d (M, Δ) = M H$ .

Ví dụ: Cho hình chóp tam giác $S . A B C$ với $S A$ vuông góc với $(A B C)$ và $S A = 3 a .$ Diện tích tam giác $A B C$ bằng $2 a^{2}, B C = a$ . Khoảng cách từ $S$ đến $B C$ bằng bao nhiêu?

A. $2 a .$

B. $4 a .$

C. $3 a .$

D. $5 a .$

Hướng dẫn giải:

Kẻ $A H$ vuông góc với $B C :$ $S_{Δ A B C} = \frac{1}{2} A H . B C \Rightarrow A H = \frac{2. S_{Δ A B C}}{B C} = \frac{4 a^{2}}{a} = 4 a$

Ta có: $S A ⊥ (A B C) \Rightarrow S A ⊥ B C$

Lại có $A H ⊥ B C$ nên $B C ⊥ (S A H) \Rightarrow B C ⊥ S H$

Do đó khoảng cách từ $S$ đến $B C$ chính là $S H .$

Dựa vào tam giác vuông $Δ S A H$ ta có $S H = \sqrt{S A^{2} + A H^{2}} = \sqrt{{(3 a)}^{2} + {(4 a)}^{2}} = 5 a$

Phương pháp 2:

Để tính được khoảng từ điểm M đến mặt phẳng (α) thì điều quan trọng nhất là ta phải xác định được hình chiếu của điểm M trên (a ).

Phương pháp này, chúng tôi chia ra làm 3 trường hợp sau (minh hoạ bằng hình vẽ): TH 1: A là chân đường cao, tức là A \[ \equiv \] H .

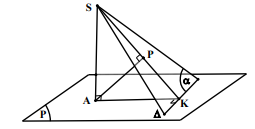
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 1)

Bước 1: Dựng AK $⊥$ D => D $⊥$ (SAK)

=> (a ) $⊥$ (SAK) và (a) Ç (SAK) = SK.

Bước 2: Dựng AP $⊥$ SK => AP $⊥$ (a)

=> d (A; (a)) = AP.

TH 2: Dựng đường thẳng AH, AH || (a ) .

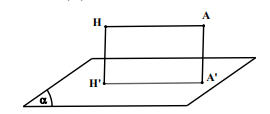
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 2)

Lúc đó : d(A(a)) = d(H,(a)).

TH 3: Dựng đường thẳng AH, AH \[ \cap \](a) = I

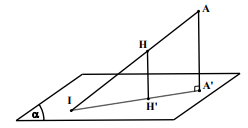
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 3)

Lúc đó: \[\frac{{d(A,(\alpha ))}}{{d(H,(\alpha ))}} = \frac{{IA}}{{IH}} \Rightarrow d(A,(\alpha )) = \frac{{IA}}{{IH}}.d(H,\alpha ))\]

Một kết quả có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng đối với tứ diện vuông (tương tư như hệ thức lượng trong tam giác vuông) là:

Nếu tứ diện OABC có OA, OB, OC đôi một vuông góc và có đường cao OH thì

\[\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\]

3. Bài tập vận dụng

Câu 1: Cho hình chóp S.ABC trong đó SA, AB , BC vuông góc với nhau từng đôi một. Biết SA = \[a\sqrt 3 \] , AB = \[a\sqrt 3 \] . Khoảng cách từ A đến (SBC) bằng

A. \[\frac{{a\sqrt 3 }}{2}\]

B. \[\frac{{a\sqrt 2 }}{3}\]

C. \[\frac{{2a\sqrt 5 }}{5}\]

D. \[\frac{{a\sqrt 6 }}{2}\]

Hướng dẫn giải:

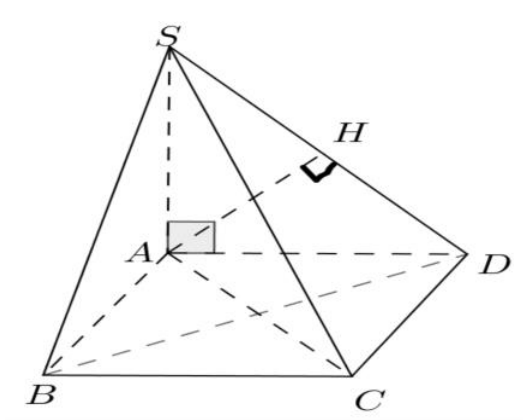
Chọn D.

Kẻ AH $⊥$ SB. Ta có \[\left\{ {\begin{array}{*{20}{c}}{BC \bot SA}\\{BC \bot AB}\end{array} \Rightarrow BC \bot (SAB)} \right. \Rightarrow BC \bot AH\].

Suy ra AH $⊥$ (SBC) => d(A, (SBC)) = AH.

Trong tam giác vuông SAB ta có:

\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Rightarrow AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + AB{}^2} }} = \frac{{\sqrt 6 a}}{2}.\]

Câu 2: Cho hình chóp S.ABCD có SA $⊥$ (ABCD) , đáy ABCD là hình chữ nhật. Biết AD = 2a , SA = a. Khoảng cách từ A đến (SCD) bằng:

A. \[\frac{{3a\sqrt 2 }}{2}\]

B. \[\frac{{2a\sqrt 3 }}{3}\]

C. \[\frac{{2a}}{{\sqrt 5 }}\]

D. \[\frac{{3a}}{{\sqrt 7 }}\]

Hướng dẫn giải:

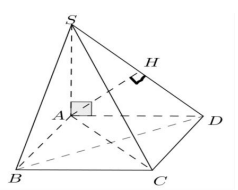
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 5)

Chọn C.

Kẻ AH $⊥$ SD , mà vì CD $⊥$ (SAD)

=> CD $⊥$ AH nên d (A;(SCD)) = AH.

Trong tam giác vuông SAD ta có:

\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} \Rightarrow AH = \frac{{SA.AD}}{{\sqrt {S{A^2} + AD{}^2} }} = \frac{{2a}}{{\sqrt 5 }}.\].

Câu 3: Cho hình chóp tam giác đều S.ABC cạnh đáy bằng 2a và chiều cao bằng \[a\sqrt 3 \] . Tính khoảng cách từ tâm O của đáy ABC đến một mặt bên:

A. \[\frac{{a\sqrt 5 }}{2}\]

B. \[\frac{{2a\sqrt 3 }}{3}\]

C. \[a\sqrt {\frac{3}{{10}}} \]

D. \[a\sqrt {\frac{2}{5}} \]

Hướng dẫn giải:

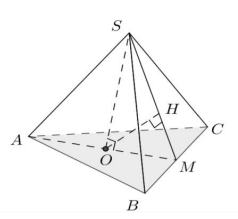
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 6)

Chọn C.

SO $⊥$ (ABC), với O là trọng tâm của tam giác ABC . M là trung điểm của BC . Kẻ OH ^ SM , ta có \[\left\{ {\begin{array}{*{20}{c}}{BC \bot SO}\\{BC \bot MO}\end{array} \Rightarrow BC \bot (SOM)} \right. \Rightarrow BC \bot OH\]

nên suy ra d(O;(SBC)) = OH. Ta có OM = \[\frac{1}{3}AM = \frac{{a\sqrt 3 }}{3}\]

\[\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} \Rightarrow OH = \frac{{SO.OM}}{{\sqrt {S{O^2} + OM{}^2} }} = \sqrt {\frac{3}{{10}}} a.\]

Câu 4: Cho tứ diện đều ABCD có cạnh bằng a . Khoảng cách từ A đến (BCD) bằng:

A. \[\frac{{a\sqrt 6 }}{2}\]

B. \[\frac{{a\sqrt 6 }}{3}\]

C. \[\frac{{a\sqrt 3 }}{6}\]

D. \[\frac{{a\sqrt 3 }}{3}\]

Hướng dẫn giải:

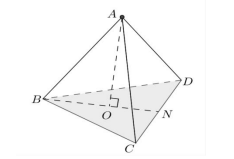
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 7)

Chọn B.

Ta có: AO $⊥$ (BCD) => O là trọng tâm tam giác BCD.

d(A;(BCD)) = AO = \[\sqrt {A{B^2} - BO{}^2} \]=\[\sqrt {{a^2} - \frac{{3{a^2}}}{9}} = \frac{{a\sqrt 6 }}{3}\]

Câu 5. Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc BAD = 60⁰. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = \[\frac{{3a}}{4}\]. Khoảng cách từ O đến mặt phẳng (SBC) là:

A. \[\frac{a}{3}\]

B. \[\frac{{3a}}{4}\]

C. \[\frac{{3a}}{8}\]

D. \[\frac{{a\sqrt 3 }}{4}\]

Hướng dẫn giải:

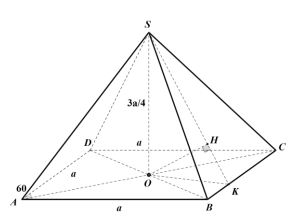
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 8)

Trong mặt phẳng (ABCD): kẻ OK $⊥$ BC (KÎBC). Mà BC $⊥$ SO nên suy ra hai mặt phẳng (SOK ) và (SBC) vuông góc nhau theo giao tuyến SK. Trong mặt phẳng (SOK): kẻ OH $⊥$ SK (HÎSK ). Suy ra: OH $⊥$ (SBC) => d(O;(SBC)) = OH.

Câu 6: Cho hai tam giác ABC và ABD nằm trong hai mặt phẳng hợp với nhau một góc 60⁰, DABC cân ở C, DABD cân ở D. Đường cao DK của DABD bằng 12 . cm Khoảng cách từ D đến ( ABC) bằng

A. \[3\sqrt 3 cm\]

B. \[6\sqrt 3 cm\]

C. 6 cm

D. \[6\sqrt 2 cm\]

Hướng dẫn giải:

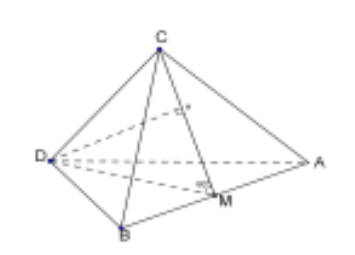
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 9)

Gọi M là trung điểm AB suy ra:

Gọi H là hình chiếu vuông góc của D lên CM

=> DH = d(D,(ABC))

DH = sin 60⁰. DM = \[6\sqrt 3 \]

Chọn đáp án B.

Câu 7: Cho hình lập phương ABCD A’B’C’D có cạnh bằng a. Khi đó khoảng cách từ tâm của hình lập phương đến mặt phẳng (BDA') bằng

A. \[a\sqrt 2 \]

B. \[a\sqrt 3 \]

C. \[\frac{{a\sqrt 3 }}{3}\]

D. \[\frac{{a\sqrt 3 }}{6}\]

Hướng dẫn giải:

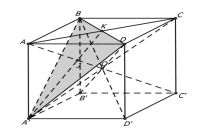
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 10)

Bài toán chứng minh AC' $⊥$ (ABD') trong sách giáo khoa đã có. Không chứng minh lại. Dễ dàng tìm được AC’ = \[a\sqrt 3 \]

d(O,(A’BD) = OJ = \[\frac{1}{6}\]AC’ = \[\frac{{a\sqrt 3 }}{6}\]

Câu 8: Cho hình lập phương ABCD.A’B’C’D cạnh a. Khoảng cách từ A đến (BDA' ) bằng

A. \[\frac{{a\sqrt 2 }}{2}\]

B. \[\frac{{a\sqrt 3 }}{3}\]

C. \[\frac{{a\sqrt 3 }}{2}\]

D. \[\frac{{a\sqrt 6 }}{3}\]

Hướng dẫn giải:

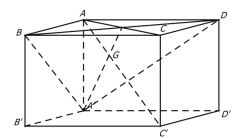
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 11)

Ta có:

\[\begin{array}{l}\left. {\begin{array}{*{20}{c}}{A'C \bot (B{\rm{D}}A')}\\{A'C \cap (B{\rm{D}}A') = {\rm{\{ }}G{\rm{\} }}}\end{array}} \right\} \Rightarrow d(A,(B{\rm{D}}A')) = AG = \frac{1}{3}AC'\\ \Rightarrow d(A,(BCA')) = \frac{{a\sqrt 3 }}{3}\end{array}\]

Đáp án B.

Câu 9: Cho hình lập phương ABCD.A’B’C’D cạnh a. Khoảng cách từ A đến (B’CD') bằng

A. \[\frac{{a\sqrt 2 }}{2}\]

B. \[\frac{{a\sqrt 3 }}{3}\]

C. \[\frac{{2a\sqrt 3 }}{3}\]

D. \[\frac{{a\sqrt 6 }}{3}\]

Hướng dẫn giải:

Ta có: AB’ = AC = AD = B’D’ = B’C = CD’ = \[a\sqrt 2 \]. Nên tứ diện AB’CD’ là tứ diện đều. Gọi I là trung điểm BC' , G là trọng tâm tam giác B’CD’. Khi đó ta có: d(A;(B’CD)) = AG. Vì tam giác B’CD’ đều nên D’I = \[a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\]

Theo tính chất trọng tâm ta có: D’G = \[\frac{2}{3}D'I = \frac{{a\sqrt 6 }}{3}\]

Trong tam giác vuông AGD' có:

\[AG = \sqrt {D'{A^2} - D'{G^2}} = \sqrt {{{\left( {a\sqrt 2 } \right)}^2} - {{\left( {\frac{{a\sqrt 6 }}{3}} \right)}^2}} = \frac{{2a\sqrt 3 }}{3}\]

Chọn C.

Câu 10: Cho hình chóp S ABC có đáy ABC là tam giác vuông cân tại A với AB = a. Mặt bên chứa BC của hình chóp vuông góc với mặt đáy, hai mặt bên còn lại đều tạo với mặt đáy một góc 45⁰ . Tính khoảng cách từ điểm S đến mặt phẳng đáy (ABC) .

A. \[\frac{a}{2}\]

B. \[\frac{{a\sqrt 2 }}{2}\]

C. \[\frac{{a\sqrt 3 }}{2}\]

D. \[\frac{{3a}}{2}\]

Hướng dẫn giải:

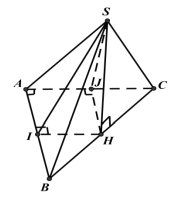
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 12)

Gọi H là hình chiếu của S lên ( ABC) , vì mặt bên (SBC) vuông góc với (ABC) nên H Î BC. Dựng HI $⊥$ AB, HJ $⊥$ AC, theo đề bài ta có SIH = SJH = 45⁰ . Do đó tam giác SHI = SHJ (cạnh góc vuông - góc nhọn)

Suy ra HI = HJ. Lại có B = C => DBIH = DCJH => HB = HC.

Vậy H trùng với trung điểm của BC . Từ đó ta có HI là đường trung bình của tam giác ABC nên HI = \[\frac{{AC}}{2} = \frac{a}{2}\]

Tam giác SHI vuông tại H và có SIH = SHI = 45⁰ Þ D SHI vuông cân.

Do đó: SH = HI = \[\frac{a}{2}\].Chọn đáp án A.

Câu 11: Cho hình chóp tam giác đều S ABC có cạnh bên bằng b, cạnh đáy bằng d với d < \[b\sqrt 3 \]. Hãy chọn khẳng định đúng trong các khẳng định bên dưới.

A. \[d(S,(ABC)) = \sqrt {{b^2} - \frac{1}{2}{d^2}} \]

B. \[d(S,(ABC)) = \sqrt {{b^2} - {d^2}} \]

C. \[d(S,(ABC)) = \sqrt {{b^2} - \frac{1}{3}{d^2}} \]

D. \[d(S,(ABC)) = \sqrt {{b^2} + {d^2}} \]

Hướng dẫn giải:

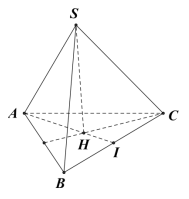
35 Bài tập trắc nghiệm về tính khoảng cách từ điểm đường thẳng, mặt phẳng có lời giải chi tiết (ảnh 13)

Gọi I là trung điểm của BC , H là trọng tâm tam giác ABC . Do S.ABC là hình chóp đều nên SH $⊥$ (ABC) => d(S,(ABC)) = SH.

Ta có AI = \[\sqrt {A{B^2} - B{I^2}} = \sqrt {{d^2} - \frac{{{d^2}}}{4}} = \frac{{d\sqrt 3 }}{2}\]

\[AH = \frac{2}{3}AI = \frac{{d\sqrt 3 }}{3} \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{b^2} - \frac{{{d^2}}}{3}} \]

Chọn C.

Tài liệu có 18 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm