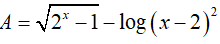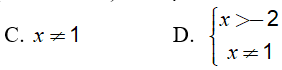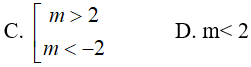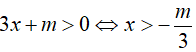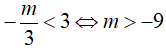Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Điều kiện để biểu thức logarit xác định và bài tập vận dụng, tài liệu bao gồm lý thuyết và các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Điều kiện để biểu thức logarit xác định và bài tập vận dụng
- Hàm số logarit cơ số là hàm số có dạng .
- Hàm số logarit có đạo hàm tại và
(đặc biệt )
- Giới hạn liên quan .
- Đạo hàm:
(đặc biệt )
Khảo sát :
- TXĐ:
- Chiều biến thiên:
+ Nếu thì hàm đồng biến trên .
+ Nếu thì hàm nghịch biến trên .
- Đồ thị:
+ Đồ thị hàm số có tiệm cận đứng .
+ Đồ thị hàm số luôn đi qua các điểm và .
+ Đồ thị nằm hoàn toàn phía bên phải trục tung vì .
+ Dáng đồ thị:
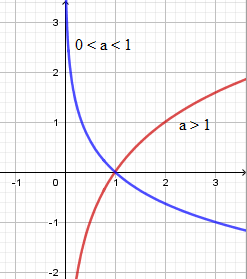
2. Điều kiện hàm logarit
Xét hàm số , ta có 3 điều kiện hàm logarit ở dạng tổng quát như sau:
-
- Xét trường hợp hàm số điều kiện . Nếu chứa biến thì ta bổ sung điều kiện
- Xét trường hợp đặc biệt: điều kiện >0 nếu n lẻ; nếu n chẵn.
Tổng quát lại:
thì điều kiện xác định là và xác định.
3. Phương pháp giải
* Để biểu thức logaf(x) xác định thì cần :
+ Cơ số a > 0 và a ≠ 1
+ f(x) > 0
* Chú ý : Xét tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0) có Δ = b2 − 4ac.
• Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a.
• Nếu Δ > 0 thì phương trình f(x)= 0 có hai nghiệm x1 ; x2.
+ Trường hợp 1 : a > 0 thì f(x) > 0 khi x ∈ (−∞; x1) ∪ (x2; +∞) và f(x) < 0 khi x ∈ (x1; x2)
+ Trường hợp 2. a < 0 thì f(x) < 0 khi x ∈ (−∞; x1) ∪ (x2; +∞) và f(x)> 0 khi x ∈ (x1; x2)
4. Bài tập vận dụng
Bài 1. Với giá trị nào của x thì biểu thức log2(4x − 2) xác định ?
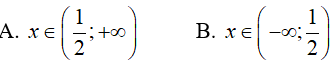
Đáp án: A
Điều kiện để biểu thức log2(4x − 2) xác định là:
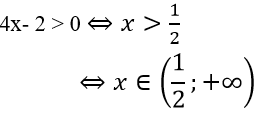
Bài 2. Tìm tập xác định của biểu thức
A. D = (2; +∞) B. D = [0; +∞)
C. D = [0; +∞)\{2} D. (0; +∞)\{2}
Đáp án: C
Biểu thức đã cho xác định
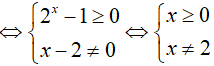
Vậy tập xác định của biểu thức là D = [0; +∞)\{2} .
Bài 3. Với giá trị nào của x thì biểu thức C = ln (x2 − 5x +6) xác định?
A. x ∈ (−∞; 2)∪(3; +∞) B. x ∈ [2; 3]. C. x ∈ R\(2; 3) D. x ∈ R\{2;3}
Đáp án: A
Điều kiện xác định: x2 − 5x + 6 > 0
⇔ x ∈ (−∞; 2)∪(3; +∞)
Bài 4. Với giá trị nào của x thì biểu thức: f(x) = log7 ( x3 − 3x + 2 ) xác định?

Đáp án: D
Biểu thức có nghĩa khi và chỉ khi:
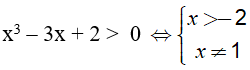
Bài 5. Điều kiện xác định của biểu thức 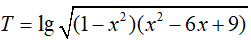
A. x < 1 hoặc x > 3 B. x > 3
C. −1 < x < 1 D. x > 1
Đáp án: C
Biểu thức có nghĩa khi và chỉ khi:
(1 − x2).(x2 − 6x + 9) > 0 ⇔ (1 − x2).(x − 3)2 > 0
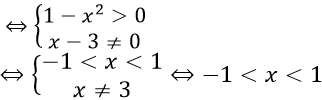
Bài 6. Với giá trị nào của m thì biểu thức f(x) = log√5(x − m) xác định với mọi x ∈ (−3; +∞)?
A. m > −3 B. m < −3 C. m ≤ −3. D. m ≥ −3.
Đáp án: C
Biểu thức f(x) xác định khi và chỉ khi: x − m > 0 ⇔ x > m.
Để f(x) xác định với mọi x ∈ (−3; +∞) thì m ≤ −3
Bài 7. Biểu thức lg(x2 − 2mx + 4) có nghĩa với mọi x ∈ R khi
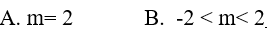
Đáp án: B
Biểu thức lg(x2 − 2mx + 4) có nghĩa với mọi số thực x khi và chỉ khi :
x2 − 2mx+ 4 > 0 với mọi x.
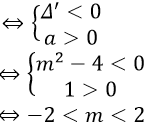
Bài 8. Biểu thức A= log2 (ax2 − 4x + 1) có nghĩa với mọi x ∈ R khi
A. 0 < a < 4 B. a > 0 C. a > 4 D. a ∈ ∅ .
Đáp án: A
Biểu thức A= log2(ax2 − 4x + 1) có nghĩa với mọi x ∈ R ⇔ ax2 − 4x + 1 > 0, ∀x ∈ R.
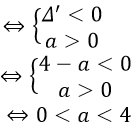
Bài 9. Với giá trị nào của m thì biểu thức f(x) =124 + 113log2(3x + m) xác định với mọi x ∈ (3; +∞)?
A. m > −3 B. m > −9 C. m < −9 D. m < −3
Đáp án: A
Biểu thức f(x) xác định khi và chỉ khi
Để f(x) xác định với mọi x ∈ (3; +∞) thì
Xem thêm các nội dung khác: