Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Tích có hướng của hai vecto trong không gian: Định nghĩa, công thức và bài tập vận dụng, tài liệu gồm đầy đủ về lý thuyết Tích có hướng của hai vecto trong không gian, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Tích có hướng của hai vecto trong không gian: Định nghĩa, công thức và bài tập vận dụng

A. Lý thuyết

1. Định nghĩa Tích có hướng của hai vectơ

Trong không gian Oxyz cho hai vectơ $\overrightarrow{a}=(a_1;a_2;a_3)$, $\overrightarrow{b}=(b_1;b_2;b_3)$. Tích có hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b},$ kí hiệu là $\left[\overrightarrow{a},\overrightarrow{b}\right]$, được xác định bởi

$$\begin{gathered} \left[\overrightarrow{a},\overrightarrow{b}\right]=\left(\left|\begin{array}{cc}{a}_2& a_3\\ b_2& b_3\end{array}\right|;\left|\begin{array}{cc}{a}_3& a_1\\ b_3& b_1\end{array}\right|;\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|\right) \\ =\left(a_2{b}_3-a_3{b}_2;a_3{b}_1-a_1{b}_3;a_1{b}_2-a_2{b}_1\right) \end{gathered}$$

Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

2. Tính chất của tích có hướng

Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ $\overrightarrow{AB};\overrightarrow{AC};\overrightarrow{AD}$ không đồng phẳng hay $\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AD}\ne 0$ và 4 điểm A, B, C, D đồng phẳng khi $\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AD}=0.$

3. Ứng dụng của tích có hướng

+ Điều kiện đồng phẳng của ba vecto:

$\overrightarrow{a}; \overrightarrow{b}$ và $\overrightarrow{c}$đồng phẳng <=> $\left[\begin{array}{cc}\overrightarrow{a},& \overrightarrow{b}\end{array}\right].\overrightarrow{c}=0$

+ Diện tích hình bình hành ABCD:

$S_{ABCD}=\left|\left[\begin{array}{cc}\overrightarrow{AB},& \overrightarrow{AD}\end{array}\right]\right|$

+ Diện tích tam giác ABC:

$S_{ABC}\frac{1}{2}\left|\left[\begin{array}{cc}\overrightarrow{AB},& \overrightarrow{AC}\end{array}\right]\right|$

+ Thể tích khối hộp ABCD.A’B’C’D’:

$V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}=|\left[\overrightarrow{AB},\overrightarrow{AD}\right].\overrightarrow{AA\text{'}|}$

+ Thể tích tứ diện ABCD

$V_{ABCD}=\frac{1}{3}|\left[\overrightarrow{AB},\overrightarrow{AC}\right].\overrightarrow{AD}|$

B. Các dạng bài tập về Tích có hướng

Tích có hướng của hai vectơ thường sử dụng để tính diện tích tam giác; tính thể tích khối tứ diện, thể tích hình hộp; chứng minh các vectơ đồng phẳng – không đồng phẳng, chứng minh các vectơ cùng phương.

Dạng 1: Tính tích có hướng của hai vectơ

Phương pháp giải: Cho hai vectơ $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ và $\overrightarrow{b}=\left(b_1;b_2;b_3\right)$, khi đó:

$$\begin{gathered} \left[\overrightarrow{a},\overrightarrow{b}\right]=\left(\left|\begin{array}{cc}{a}_2& a_3\\ b_2& b_3\end{array}\right|;\left|\begin{array}{cc}{a}_3& a_1\\ b_3& b_1\end{array}\right|;\left|\begin{array}{cc}{a}_1& a_2\\ b_1& b_2\end{array}\right|\right) \\ =\left(a_2{b}_3-a_3{b}_2;a_3{b}_1-a_1{b}_3;a_1{b}_2-a_2{b}_1\right) \end{gathered}$$

Ví dụ: Trong không gian với hệ trục tọa độ Oxyz, cho $\overrightarrow{a}=\left(3;2;1\right),$$\overrightarrow{b}=\left(3;2;5\right)$. Khi đó $\left[\overrightarrow{a},\overrightarrow{b}\right]$ có tọa độ bằng

A. $\left(8;-12;5\right)$

B. $\left(8;-12;0\right)$

C. $\left(0;8;12\right)$

D. $\left(0;8;-12\right)$

Hướng dẫn giải

$$\begin{gathered} \left\{\begin{array}{l}\overrightarrow{a}=\left(3;2;1\right)\\ \overrightarrow{b}=\left(3;2;5\right)\end{array}\right. \\ \Rightarrow \left[\overrightarrow{a},\overrightarrow{b}\right] \\ =\left(2.5-2.1;1.3-3.5;3.2-3.2\right) \\ =\left(8;-12;0\right) \end{gathered}$$

Chọn B.

Dạng 2: Tìm điều kiện để ba vectơ đồng phẳng

Phương pháp giải: $\overrightarrow{a},\overrightarrow{b}$ và $\overrightarrow{c}$ đồng phẳng $[\overrightarrow{a},\overrightarrow{b}].\overrightarrow{c}=0$

Ví dụ: Trong không gian với hệ tọa độ Oxyz cho vectơ $\overrightarrow{a}=\left(1;m;2\right);$$\hspace{0.17em}\overrightarrow{b}=\left(m+1;2;1\right);$$\overrightarrow{c}=\left(0;m-2;2\right)$. Giá trị của m để $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ đồng phẳng là

A. $\frac{2}{5}$

B. $\frac{-2}{5}$

C. $\frac{1}{5}$

D. 1.

Hướng dẫn giải

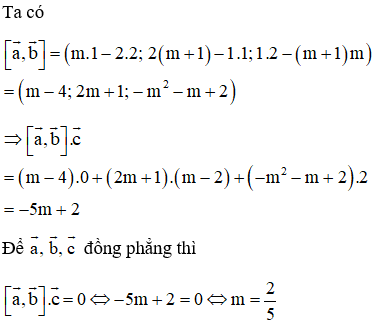
Chọn A.

Dạng 3: Tính diện tích một số hình phẳng

Phương pháp giải:

Áp dụng các công thức sau:

+) Diện tích hình bình hành ABCD:

$S_{ABCD}=\left|\left[\overrightarrow{AB},\overrightarrow{AD}\right]\right|$

+) Diện tích tam giác ABC:

$S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB},\overrightarrow{AC}\right]\right|$

Ví dụ: Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC với A (1; 2; 1), B (2; 1; 3) và C (3; 2; 2). Diện tích tam giác ABC bằng

A. $\frac{\sqrt{11}}{2}$

B. $\sqrt{3}$

C. $\frac{\sqrt{13}}{2}$

D. $\frac{\sqrt{14}}{2}$

Hướng dẫn giải

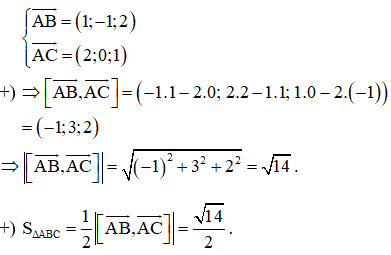
Chọn D.

Dạng 4: Tính thể tích khối hộp và tứ diện

Phương pháp giải:

Áp dụng các công thức sau:

+) Thể tích khối hộp ABCD. A’B’C’D’:

$V_{ABCD.A\text{'}B\text{'}C\text{'}D\text{'}}=\left|[\overrightarrow{AB},\overrightarrow{AD}].\overrightarrow{A{A}^{\text{'}}}\right|$

+) Thể tích tứ diện ABCD:

$V_{ABCD}=\frac{1}{6}\left|[\overrightarrow{AB},\overrightarrow{AC}].\overrightarrow{AD}\right|$

Ví dụ: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD với A (1; 2; 1), B (2; 1; 3), C (3; 2; 2), D (1; 1; 1). Thể tích của tứ diện ABCD bằng

A. 1

B. 2

C. $\frac{1}{2}$

D. 3.

Hướng dẫn giải

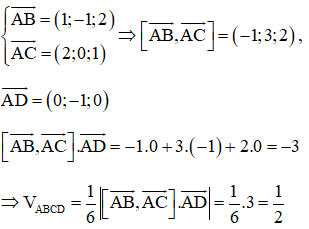
Chọn C.

C. Bài tập về Tích có hướng

1. Bài tập vận dụng

Câu 1: Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ $\overrightarrow{a}=\left(2;1;0\right)$ và $\overrightarrow{b}=\left(-1;0;-2\right)$. Tính $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)$.

A. $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=-\frac{2}{25}$

B. $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=-\frac{2}{5}$

C. $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{2}{25}$

D. $\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=\frac{2}{5}$

Câu 2: Trong không gian với hệ trục tọa độ Oxyz, cho $\overrightarrow{a}=\left(1;-2;1\right),$$\overrightarrow{b}=\left(2;-4;2\right)$. Khi đó $\left[\overrightarrow{a},\overrightarrow{b}\right]$ có tọa độ bằng

A. (0 ; 0 ; 0).

B. (1 ; 1 ; 1)

C. (2 ; 8 ; 2)

D. (1 ; -2 ; 1).

Câu 3: Cho bốn véc tơ $\overrightarrow{a}=\left(-1;1;0\right)$,$\overrightarrow{b}=\left(1;1;0\right)$ ,$\overrightarrow{c}=\left(1;1;1\right)$, $\overrightarrow{d}=\left(2;0;1\right)$. Chọn mệnh đề đúng.

A.$\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ đồng phẳng.

B. $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{d}$ đồng phẳng.

C. $\overrightarrow{a}$, $\overrightarrow{c}$, $\overrightarrow{d}$ đồng phẳng.

D. $\overrightarrow{d}$, $\overrightarrow{b}$, $\overrightarrow{c}$ đồng phẳng.

Câu 4: Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A (1; 1; 1), B (4; 3; 2), C (5; 2; 1). Diện tích tam giác ABC là

A. $\frac{\sqrt{42}}{4}$

B. $\sqrt{42}$

C. $2\sqrt{42}$

D. $\frac{\sqrt{42}}{2}$

Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có A (1; 0; 1), B (2; 0; -1), C (0; 1; 3), D (3; 1; 1). Thể tích khối tứ diện ABCD là

A.$V=\frac{2}{3}$

B. $V=\frac{4}{3}$

C. V = 4

D. V = 2.

Câu 6: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD. A’B’C’D’ có A (-1; 0; 2), B (1; 1; -1), D (0; 1; 1), A’ (2; -1; 0). Thể tích V của khối hình hộp ABCD. A’B’C’D’ là

A. V = 1.

B. V = 4.

C. V = 5.

D. V = 6.

Câu 7: Cho ba vectơ $\overrightarrow{a}=\left(4;2;5\right),\overrightarrow{b}=\left(3;1;3\right),\overrightarrow{c}=\left(2;0;1\right)$. Chọn mệnh đề đúng:

A. Ba vectơ đồng phẳng

B. Ba vectơ không đồng phẳng.

C. Ba vectơ cùng phương

D. $\overrightarrow{c}=\left[\overrightarrow{a},\overrightarrow{b}\right]$

Câu 8: Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(-2;2;1), B(1;0;2), C(-1;2;3). Diện tích tam giác ABC là:

A. /2

B. 

C. 

D. 5/2

Câu 9: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0). Bán kính đường tròn nội tiếp tam giác ABC là:

A. 

B. 

C. 

D. 

Câu 10: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(1;0;0), B(0;0;1), C(2;1;1). Độ dài đường cao của tam giác ABC kẻ từ A là:

A. ( )/5

B. ()/5

C. ()/5

D. ()/2

Câu 11: Cho A(1;-2;0), B(3;3;2), C(-1;2;2), D(3;3;1). Thể tích của tứ diện ABCD bằng

A. 3   

B. 4

C. 5   

D. 6

Câu 12: Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Độ dài đường cao AH của tứ diện ABCD là:

A. 5   

B. 6

C. 7   

D. 9

2. Bài tập tự luyện

Bài 1. Trong không gian Oxyz, cho ba điểm A(-2; 2; 1), B(1; 0; 2), C(-1; 2; 3). Tính diện tích tam giác ABC.

Bài 2. Trong không gian với hệ toạ độ Oxyz, cho hình chóp S.OAMN với S(0; 0; 1), A(1; 1; 0), M(m; 0; 0), N(0; n; 0). Trong đó m > 0, n > 0 và m + n = 6. Tính thể tích hình chóp S.OAMN.

Bài 3. Trong không gian với hệ toạ độ Oxyz, cho bốn điểm A(-1; -2; 4), B(-4; -2; 0), C(3; -2; 1), D(1; 1; 1). Tính độ dài đường cao của tứ diện kẻ từ D.

Bài 4. Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC biết A(2; -1; 6), B(-3; -1; -4), C(5; -1; 0). Tính bán kính đường tròn nội tiếp tam giác ABC.

Bài 5. Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD biết A(2; -1; 1), B(5; 5; 4), C(3; 2; -1), D(4; 1; 3). Tính thể tích tứ diện ABCD.