Tailieumoi.vn xin giới thiệu đến bạn đọc bài viết về Cách viết Phương trình chính tắc của elip. Bài viết nêu đầy để về phương pháp giải và một số bài tập vận dụng giúp các bạn ôn luyện kiến thức, rèn kĩ năng là bài để học tốt môn Toán hơn.

Cách viết Phương trình chính tắc của elip và bài tập vận dụng

A. Phương pháp giải

- Từ các thành phần đã biết, áp dụng các công thức liên quan ta tìm được phương trình chính tắc của elip:

 = 1

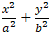
- Các hệ thức:

+ 0 < b < a; 0 < c < a

+ c² = a² - b²

+ F₁F₂ = 2c ( tiêu cự)

+ A₁A₂ = 2a (độ dài trục lớn) .

+ B₁B₂ = 2b( độ dài trục nhỏ).

+ M thuộc ( E) ⇔ MF₁ MF₂= 2a.

B. Bài tập vận dụng

Ví dụ 1: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip ( E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình nào sau đây là phương trình của elip (E)?

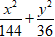
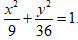
A.  = 1         B.     

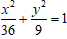
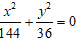
C.          D.         

Lời giải

Phương trình chính tắc của elip có dạng 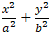 = 1 (a,b > 0).

Ta có độ dài trục lớn bằng 12 nên 2a= 12 ⇒ a= 6

Vậy phương trình của Elip là: 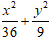     = 1.

Chọn C

Ví dụ 2: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E)?

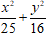
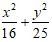
A.  = 1     B.  = 1

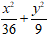
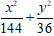
C.  = 1     D.  = 1

Lời giải

Ta có:

+ Độ dài trục lớn bằng 10 nên 2a = 10 ⇒ a = 5

+ Độ dài tiêu cự là 6 nên 2c = 6 ⇒ c = 3

⇒ b² = a² – c² = 52- 32 = 16

Vậy phương trình của Elip là: 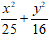     = 1.

Chọn A

Ví dụ 3: Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10. Phương trình nào sau đây là phương trình của elip (E)

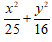
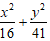
A.  = 1     B.  = 1

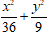
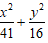
C.  = 1     D.  = 1

Lời giải

Ta có:

+ Độ dài trục nhỏ là 8 nên 2b= 8 ⇔ b= 4.

+ Độ dài tiêu cự bằng 10 nên 2c= 10 ⇔ c= 5

Suy ra : a² = b² + c² = 42+ 52 = 41

Vậy phương trình của Elip là: 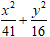 = 1    

Chọn D

Ví dụ 4: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng 4√3.

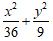
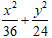
A.  = 1     B.  = 1

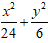
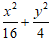
C.  = 1     D.  = 1

Lời giải

Gọi phương trình chính tắc của Elip 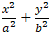 = 1 (a,b > 0). .

Ta có  ⇒  ⇒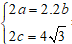 

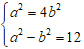
⇒ Phương trình elip ( E) : 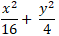     = 1

Chọn D

Ví dụ 5: Tìm phương trình chính tắc của Elip có trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng 1/3 .

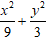
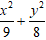
A.  = 1     B.  = 1

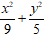
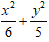
C.  = 1     D.  = 1

Lời giải

Gọi phương trình chính tắc của Elip có dạng 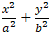 = 1 (a,b > 0).

Tỉ số của tiêu cự với độ dài trục lớn bằng 1/3 nên 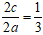 ⇒ a = 3c.

Lại có trục lớn bằng 6 nên 2a= 6 ⇔ a= 3

Mà a = 3c nên c = 1 ⇒ b² = a² - c² = 8

⇒ Phương trình chính tắc elip ( E) : 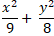    = 1

Chọn B

Ví dụ 6: Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là

M( 4; 3)

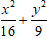
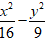
A.  = 1     B.  = 1

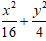
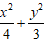
C.  = 1     D.  = 1

Lời giải

Gọi phương trình chính tắc của Elip có dạng 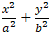 = 1 (a,b > 0).

Các đỉnh của hình chữ nhật cơ sở có tọa độ: ( a;b) ; ( a; - b); ( -a; -b) và (-a; b).

Ta có M(4; 3) là một đỉnh của hình chữ nhật cơ sở nên chọn  .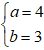

⇒ Phương trình elip ( E) : 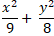     = 1.

Chọn A

Ví dụ 7: Phương trình của Elip có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là:

A. 9x² + 16y² = 144     B. 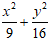 = 1

C. 9x² + 16y² = 1     D. 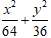 = 1

Lời giải

Gọi phương trình chính tắc của Elip có dạng 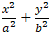 = 1 (a,b > 0).

Ta có độ dài trục lớn là 8 và độ dài trục nhỏ bằng 6 nên:      ⇒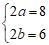 

⇒ Phương trình elip ( E) : 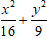 = 1 hay 9x² + 16y² = 144

Chọn A

Ví dụ 8: Phương trình chính tắc của Elip có độ dài trục lớn bằng 26, tâm sai e = 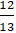 là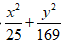

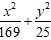
A.  = 1     B.  = 1

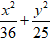
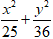
C.  = 1     D.  = 1

Lời giải

+ Ta có độ dài trục lớn là 26 nên 2a = 26 ⇔ a = 13

+ Tâm sai của elip (E): e = 

⇔ c = 12

⇒ b² = a² – c² = 132- 122 = 25

Phương trình chính tắc của elip là: (E): 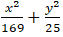     = 1.

Chọn B

Ví dụ 9: Elip có một tiêu điểm F( -2; 0) và tích độ dài trục lớn với trục bé bằng 12√5. Phương trình chính tắc của elip là:

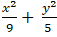
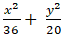
A.  = 1     B.  = 1

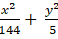
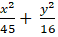
C.  = 1     D.  = 1

Lời giải

Elip ( E) có một tiêu điểm F(-2; 0) nên c = 2.

Elip ( E) có tích độ dài trục lớn với trục bé bằng 12√5 nên :

2a. 2b = 12√5 hay ab = 3√5 ⇒a = 

Lại có: a² - b² = c² nên 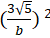 - b² = 4

⇔ 45- b⁴ = 4b² ⇔ 

Với b² = 5 thì b = √5 ⇒ a = 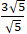 = 3.

⇒ Phương trình chính tắc của Elip là 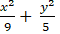     = 1.

Chọn A

Ví dụ 10: Lập phương trình chính tắc của elip có độ dài trục nhỏ bằng 12 và tỉ số của tiêu cự với độ dài trục lớn bằng 4/5.

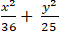
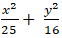
A.  = 1     B.  = 1

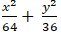
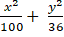
C.  = 1     D.  = 1

Lời giải

Gọi phương trình chính tắc của Elip là: 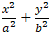 = 1 (a,b > 0).

Độ dài trục nhỏ của Elip là 12 suy ra 2b = 12 ⇒ b = 6. ( 1)

Tiêu cự của Elip là 2c; độ dài trục lớn là 2a theo giả thiết ta có:

 nên c =  (2)

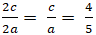
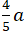
Mặt khác a² - b² = c² ( 3)

Thay (1); ( 2) vào ( 3) ta được: a² - 62 = 

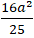
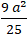
⇔ a² - 36=  ⇔  = 36

⇔ a² = 100

Vậy phương trình cần tìm là ( E) : 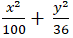     = 1.

Chọn D