Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Góc giữa đường thẳng và mặt phẳng Toán lớp 12, tài liệu bao gồm 12 trang, tuyển chọn các bài tập Góc giữa đường thẳng và mặt phẳng đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có lời giải, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
Góc giữa đường thẳng và mặt phẳng
1. Định nghĩa
Định nghĩa:
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của nó lên trên mặt phẳng.
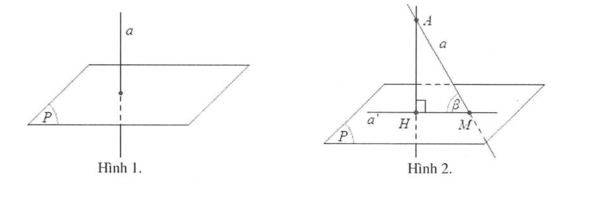
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 90 độ. (hình 1).
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và hình chiếu a' của nó lên mặt phẳng (P) (hình 2).
Chú ý: Góc giữa đường thẳng và mặt phẳng không vượt quá .
2. Phương pháp giải
Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng.
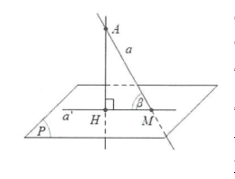
Cách tìm hình chiếu của a trên mặt phẳng (P) ta có thể làm như sau:
Tìm giao điểm
Tìm một điểm A tùy ý trên đường thẳng a và xác định hình chiếu vuông góc H của A trên mặt phẳng (P). Khi đó, là đường thẳng đi qua hai điểm A và M. Ta có
Xét tam giác vuông AMH ta có:
(trong đó là khoảng cách từ điểm A đến mặt phẳng (P)).
3. Bài tập ví dụ
Dạng 1: Góc giữa cạnh bên và mặt đáy
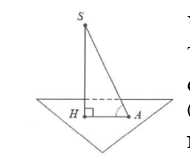
Tìm góc giữa cạnh bên SA và mặt đáy (ABC)
Gọi H là hình chiếu vuông góc của S trên mặt phẳng đáy (ABC).
Như vậy HA là hình chiếu vuông góc của SA trên (ABC).
Vậy
Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, có AB = a. Biết , SB tạo với đáy một góc 600 và M là trung điểm của BC.
a) Tính cosin góc giữa SC và mặt phẳng (ABC).
b) Tính cosin góc giữa SM và mặt phẳng (ABC).
Lời giải
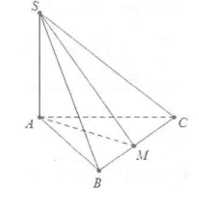
a) Do
Do đó
Ta có:
Khi đó:
b) Do
Ta có:
Khi đó
Ví dụ 2: Cho hình chóp S.ABCD, đáy là hình chữ nhật có \[AB = 2a;AD = a\]. Tam giác (SAB) đều và thuộc mặt phẳng vuông góc với đáy.
a) Tính góc giữa SB, SC và mặt phẳng (ABCD).
b) Gọi I là trung điểm của BC. Tính tan góc giữa SI và mặt phẳng (ABCD).
Lời giải
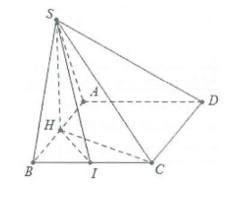
a) Gọi H là trung điểm của AB ta có: \[SH \bot AB\]
Mặt khác
\[\begin{array}{l}\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\AB = \left( {SAB} \right) \cap \left( {ABCD} \right)\end{array} \right.\\ \Rightarrow SH \bot \left( {ABCD} \right).\end{array}\]
Tam giác SAB đều cạnh 2a nên \[SH = a\sqrt 3 ,\]
\[HC = \sqrt {H{B^2} + B{C^2}} = a\sqrt 2 .\]
Do \[SH \bot \left( {ABCD} \right)\]\[ \Rightarrow \left( {\widehat {SB;\left( {ABCD} \right)}} \right) = \widehat {SBH} = 60^\circ \]
\[\left( {\widehat {SC;\left( {ABCD} \right)}} \right) = \widehat {SCH}\] và \[\tan \widehat {SCH} = \frac{{SH}}{{HC}} = \sqrt {\frac{3}{2}} .\]
b) Ta có:
\[\begin{array}{l}HI = \sqrt {H{B^2} + B{I^2}} \\ = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}.\end{array}\]
Mặt khác \[\left( {\widehat {SI;\left( {ABCD} \right)}} \right) = \widehat {SIH}\] và \[\widehat {SIH} = \frac{{SH}}{{SI}} = a\sqrt 3 :\frac{{a\sqrt 5 }}{2} = \frac{{2\sqrt {15} }}{5}.\]
Ví dụ 3: Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a, \[AD = 2a\]. Biết \[SA \bot \left( {ABCD} \right)\] và đường thẳng SB tạo với đáy một góc \[45^\circ .\]
a) Tính cosin góc tạo bởi các cạnh SC, SD và mặt đáy (ABCD).
b) Gọi I là trung điểm của CD, tính tan góc tạo bởi SI và mặt phẳng (ABCD).
Lời giải
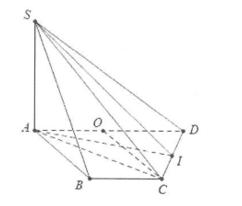
a) Gọi O là trung điểm của AD \[ \Rightarrow \] OABC là hình thoi cạnh a \[ \Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD\] vuông tại C.
Do \[SA \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 45^\circ .\]
Do đó \[SA = AB\tan 45^\circ = a.\]
\[\begin{array}{l}AC = \sqrt {A{D^2} - C{D^2}} = a\sqrt 3 \\ \Rightarrow \cos \widehat {\left( {SC;\left( {ABC} \right)} \right)} = \cos \widehat {SCA}\end{array}\]
\[\begin{array}{l} = \frac{{AC}}{{SC}} = \frac{{AC}}{{\sqrt {S{A^2} + A{C^2}} }}\\ = \frac{{a\sqrt 3 }}{{\sqrt {{a^2} + 3{a^2}} }} = \frac{{\sqrt 3 }}{2}.\end{array}\]
\[\begin{array}{l}\cos \left( {\widehat {SD;\left( {ABCD} \right)}} \right) = \cos \widehat {SDA}\\ = \frac{{AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{2}{{\sqrt 5 }}.\end{array}\]
b) Ta có:
\[\begin{array}{l}AI = \sqrt {A{C^2} + C{I^2}} \\ = \sqrt {3{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {13} }}{2}.\end{array}\]
Do đó
\[\begin{array}{l}\tan \widehat {\left( {SI;\left( {ABCD} \right)} \right)} = \tan \widehat {SIA}\\ = \frac{{SA}}{{AI}} = \frac{2}{{\sqrt {13} }}.\end{array}\]
Dạng 2: Góc giữa cạnh bên và mặt phẳng chứa đường cao

Tìm góc giữa cạnh bên SB và mặt phẳng (SHA) với \[\left( {SHA} \right) \bot \left( {ABH} \right).\]
Dựng \[BK \bot AH\], có \[BK \bot SH \Rightarrow BK \bot \left( {SHA} \right).\]
Suy ra K là hình chiếu vuông góc của B trên mặt phẳng (SAH).
Vậy \[\widehat {\left( {SB;\left( {SAH} \right)} \right)} = \widehat {\left( {SB;SK} \right)} = \widehat {BSK}.\]
Ví dụ 1: Cho hình chóp S.ABCD có đáy là hình chữ nhật có \[AB = a,AD = a\sqrt 3 ,SA \bot \left( {ABCD} \right).\]
Biết SC tạo với đáy một góc \[60^\circ \]. Tính cosin góc tạo bởi:
a) SC và mặt phẳng (SAB); SC và mặt phẳng (SAD).
b) SD và mặt phẳng (SAC).
Lời giải
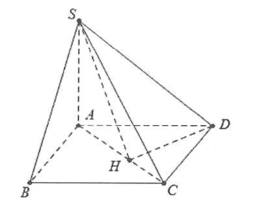
Do \[SA \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\]
Lại có:
\[\begin{array}{l}AC = \sqrt {A{B^2} + A{D^2}} = 2a\\ \Rightarrow SA = AC\tan 60^\circ = 2a\sqrt 3 .\end{array}\]
Khi đó \[\left\{ \begin{array}{l}SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt {13} \\SD = \sqrt {S{A^2} + A{D^2}} = a\sqrt {15} \\SC = \sqrt {S{A^2} + A{C^2}} = 4a.\end{array} \right.\]
Do \[\left\{ \begin{array}{l}CB \bot SA\\CB \bot AB\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\]\[ \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {CSB}.\]
Mặt khác \[\cos \widehat {CSB} = \frac{{SB}}{{SC}} = \frac{{\sqrt {13} }}{4}.\]
Tương tự \[CD \bot \left( {SAD} \right) \Rightarrow \widehat {\left( {SC;\left( {SAD} \right)} \right)} = \widehat {CSD}\] và \[\cos \widehat {SCD} = \frac{{SD}}{{SC}} = \frac{{\sqrt {15} }}{4}.\]
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a, \[BD = a\sqrt 3 ,SA \bot \left( {ABCD} \right).\]
Biết SC tạo với đáy một góc \[60^\circ \]. Tính tan góc tạo bởi:
a) SC và mặt phẳng (SAB).
b) SD và mặt phẳng (SAC).
Lời giải
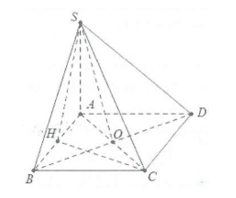
a) Ta có: \[AC \bot BD\] tại O. Khi đó \[OA = OC,OB = OD.\]
Xét tam giác vuông OAB ta có: \[\sin \widehat {OAB} = \frac{{OB}}{{AB}} = \frac{{\sqrt 3 }}{2}\]
\[ \Rightarrow \widehat {OAB} = 60^\circ \Rightarrow \Delta ABC\] đều cạnh a.
Mặt khác
\[\begin{array}{l}SA \bot \left( {ABCD} \right)\\ \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\end{array}\]
Suy ra \[SA = AC\tan 60^\circ = a\sqrt 3 .\]
Dựng \[CH \bot AB \Rightarrow CH \bot \left( {SAB} \right)\]
\[ \Rightarrow \widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {CSH}.\]
Do \[\Delta ABC\] đều cạnh a nên H là trung điểm của AB.
Ta có: \[CH = \frac{{a\sqrt 3 }}{2} \Rightarrow \tan \widehat {CSH} = \frac{{CH}}{{SH}}\] trong đó \[SH = \sqrt {S{A^2} + A{H^2}} = \frac{{a\sqrt {13} }}{2}.\]
Do đó \[\tan \widehat {CSH} = \frac{{\sqrt 3 }}{{\sqrt {13} }} = \frac{{\sqrt {39} }}{{13}}.\]
b) Ta có:
\[\left\{ \begin{array}{l}DO \bot AC\\DO \bot SA\end{array} \right. \Rightarrow \left( {\widehat {SD;\left( {SAC} \right)}} \right) = \widehat {DSO}\] và \[\tan \widehat {DSO} = \frac{{OD}}{{SO}}.\]
Trong đó
\[\begin{array}{l}OD = \frac{{a\sqrt 3 }}{2};\\SO = \sqrt {S{A^2} + O{A^2}} = \frac{{a\sqrt {13} }}{2}\\ \Rightarrow \tan \widehat {DSO} = \frac{{\sqrt {39} }}{{13}}.\end{array}\]
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, hình chiếu vuông góc của đỉnh S lên mặt đáy là điểm H thuộc cạnh AB sao cho \[\overrightarrow {HB} = - 2\overrightarrow {HA} \]. Biết \[AB = 3,AD = 6\] và \[SH = 2\]. Tính tan góc tạo bởi:
a) SA và mặt phẳng (SHD).
b) SB và mặt phẳng (SHC).
Lời giải
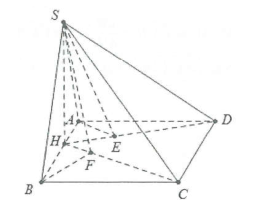
a) Ta có:
\[\begin{array}{l}AH = 1,HB = 2\\ \Rightarrow \left\{ \begin{array}{l}SA = \sqrt {S{H^2} + A{H^2}} = \sqrt 5 \\SB = \sqrt {S{H^2} + H{B^2}} = 2\sqrt 2 \end{array} \right.\end{array}\]
Dựng
\[\begin{array}{l}AE \bot DH \Rightarrow AE \bot \left( {SHD} \right)\\ \Rightarrow \widehat {\left( {SA;\left( {SHD} \right)} \right)}{\rm{ = }}\widehat {{\rm{ASE}}}\end{array}\]
Mặt khác \[AE = \frac{{AH.AD}}{{\sqrt {A{H^2} + A{D^2}} }} = \frac{6}{{\sqrt {37} }}\]
Suy ra \[\tan \widehat {{\rm{ASE}}} = \frac{{AE}}{{SA}} = \frac{6}{{\sqrt {185} }}.\]
b) Dựng \[BF \bot HC \Rightarrow BF \bot \left( {SHC} \right).\]
Khi đó \[\widehat {\left( {SB;\left( {SHC} \right)} \right)}{\rm{ = }}\widehat {BSF}\], \[BF = \frac{{BH.BC}}{{\sqrt {B{H^2} + B{C^2}} }} = \frac{{3\sqrt {10} }}{5}.\]
Ta có: \[\tan \widehat {\left( {SB;\left( {SHC} \right)} \right)} = \tan \widehat {BSF} = \frac{{BF}}{{SB}} = \frac{{3\sqrt 5 }}{{10}}.\]
Ví dụ 4: Cho hình lăng trụ \[ABCD.A'B'C'D'\] có đáy ABCD là hình chữ nhật có\[AB = 2a,AD = 2a\sqrt 3 \], hình chiếu vuông góc của \[A'\] lên mặt phẳng (ABCD) trùng với tâm O của hình chữ nhật ABCD, biết cạnh bên \[AA'\] tạo với đáy một góc \[60^\circ \]. Tính cosin góc tạo với \[A'C\] và mặt phẳng \[\left( {A'BD} \right).\]
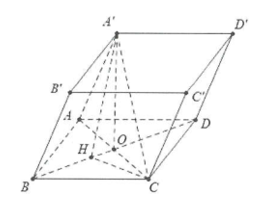
Ta có:
\[\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = 4a\\ \Rightarrow OA = 2a = OC.\end{array}\]
Do \[A'O \bot \left( {ABCD} \right)\]\[ \Rightarrow \widehat {\left( {A'O;\left( {ABCD} \right)} \right)} = \widehat {A'AO} = 60^\circ .\]
\[ \Rightarrow A'O = OA\tan 60^\circ = 2a\sqrt 3 \]
Dựng \[CH \bot BD \Rightarrow CH \bot \left( {A'BD} \right)\]
\[ \Rightarrow \widehat {\left( {A'C;\left( {A'BD} \right)} \right)} = \widehat {CA'H}.\]
Ta có: \[CH = \frac{{BC.CD}}{{\sqrt {B{C^2} + C{D^2}} }} = a\sqrt 3 .\]
\[A'C = \sqrt {O{{A'}^2} + O{C^2}} = \sqrt {12{a^2} + 4{a^2}} = 4a.\]
Suy ra
\[\begin{array}{l}\cos \widehat {CA'H} = \frac{{A'H}}{{A'C}} = \frac{{\sqrt {A'{C^2} - H{C^2}} }}{{A'C}}\\ = \frac{{\sqrt {16{a^2} - 3{a^2}} }}{{4a}} = \frac{{\sqrt {13} }}{4}.\end{array}\]
Ví dụ 5: Cho hình lăng trụ đứng \[ABC.A'B'C'\] có đáy là tam giác đều cạnh a. Tính góc tạo bởi \[A'C\] và mặt phẳng \[\left( {ABB'A'} \right)\] biết \[AA' = \frac{{a\sqrt 2 }}{2}.\]
Lời giải

Dựng \[CH \bot AB \Rightarrow CH = \frac{{a\sqrt 3 }}{2}.\]
Do
\[\begin{array}{l}\left\{ \begin{array}{l}CH \bot AB\\CH \bot AA'\end{array} \right. \Rightarrow CH \bot \left( {ABB'A'} \right)\\ \Rightarrow \widehat {\left( {A'C;\left( {ABB'A'} \right)} \right)} = \widehat {CA'H}.\end{array}\]
Lại có: \[A'H = \sqrt {A{{A'}^2} + A{H^2}} = \sqrt {\frac{{{a^2}}}{2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{4}.\]
Do đó \[\tan \widehat {CA'H} = \frac{{CH}}{{A'H}} = 1 \Rightarrow \widehat {CA'H} = 45^\circ .\]
Vậy \[\widehat {\left( {A'C;\left( {ABB'A'} \right)} \right)} = \widehat {CA'H} = 45^\circ .\]
Dạng 3: Góc giữa đường cao và mặt bên
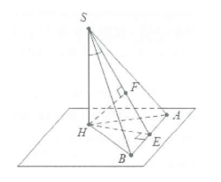
Tìm góc giữa đường cao SH và mặt phẳng (SAB).
Dựng \[HE \bot AB,HF \bot SE.\]
Ta có: \[AB \bot SH \Rightarrow AB \bot \left( {SHE} \right) \Rightarrow AB \bot HF.\]
Mặt khác \[HF \bot SE \Rightarrow HF \bot \left( {SAB} \right) \Rightarrow F\] là hình chiếu vuông góc của H trên mặt phẳng (SAB).
Vậy \[\widehat {\left( {SH;SAB} \right)} = \widehat {\left( {HF;SF} \right)} = \widehat {HSF}.\]
Ví dụ 1: Cho hình chóp S.ABC, có đáy ABC là tam giác đều cạnh 2a. Cạnh bên \[SA = a\sqrt 3 \] và vuông góc với đáy. Tính góc giữa SA và mặt phẳng (SBC).
Lời giải
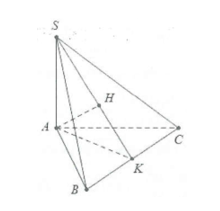
Từ A kẻ AK vuông góc với BC tại K.
Ta có : \[SA \bot BC\] và \[AK \bot BC \Rightarrow BC \bot \left( {SAK} \right).\]
Kẻ \[AH \bot SK,H \in SK\]. Mà \[BC \bot AH.\]
Suy ra \[AH \bot \left( {SBC} \right) \Rightarrow \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASH} = \widehat {ASK}.\]
Tam giác SAK vuông tại A, có \[SA = AK = a\sqrt 3 .\]
\[ \Rightarrow \] tam giác SAK vuông cân tại A nên \[ASK = 45^\circ .\]
Vậy \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = 45^\circ .\]
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật có \[AB = a,AD = 2a,SA = 2a\] và \[SA \bot \left( {ABCD} \right)\]. Tính tan góc giữa SA và các mặt phẳng (SBC), (SBD) và (SCD).
Lời giải
Do \[\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right).\]
Dựng \[AM \bot SB \Rightarrow AM \bot \left( {SBC} \right)\]
\[ \Rightarrow \] M là hình chiếu vuông góc của A trên (SBC).
Khi đó: \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASM} = \widehat {ASB} = \alpha .\]
Do đó \[\tan \alpha = \frac{{AB}}{{SA}} = \frac{1}{2}.\]
Tương tự ta có: \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASD} = \beta \] và \[\tan \beta = \frac{{AD}}{{SA}} = 1.\]
Dựng \[AE \bot BD,AF \bot SE\] ta có:
\[\left\{ \begin{array}{l}BD \bot AE\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAE} \right) \Rightarrow BD \bot AF.\]
Mặt khác
\[\begin{array}{l}AF \bot SE \Rightarrow AF \bot \left( {SBD} \right)\\ \Rightarrow \widehat {\left( {SA;\left( {SBD} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\end{array}\]
Khi đó \[\tan \widehat {ASE} = \frac{{AE}}{{SA}}\], trong đó
\[\begin{array}{l}AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt 5 }}\\ \Rightarrow \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{1}{{\sqrt 5 }}.\end{array}\]
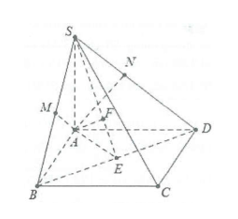
Ví dụ 3: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có \[AD = 2AB = 2CD = 2a\] và \[SA \bot \left( {ABCD} \right)\]. Biết rằng SC tạo với đáy một góc \[60^\circ \]. Tính tan góc giữa SA và các mặt phẳng (SBC), (SCD) và (SBD).
Lời giải
Ta có: \[AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \]
Do \[SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {SCA} = 60^\circ .\]
Suy ra \[SA = AC\tan 60^\circ = a\sqrt 6 .\]
Dựng \[AM \bot SB\] có \[\left\{ \begin{array}{l}BC \bot SA\\BC \bot AB\end{array} \right. \Rightarrow BC \bot AM.\]
Do đó \[AM \bot \left( {SBC} \right) \Rightarrow \] M là hình chiếu của A trên mặt phẳng (SBC).
Suy ra \[\widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASM} = \widehat {ASB}.\]
Ta có: \[\tan \widehat {ASB} = \frac{{AB}}{{SA}} = \frac{a}{{a\sqrt 6 }} = \frac{1}{{\sqrt 6 }}.\]
Gọi I là trung điểm của AD \[ \Rightarrow \] ABCI là hình vuông cạnh a \[ \Rightarrow CI = \frac{{AD}}{2} = a \Rightarrow \Delta ACD\] vuông tại C.
Khi đó \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]
Dựng \[AN \bot SC \Rightarrow \widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASN} = \widehat {ASC}.\]
Ta có: \[\tan \widehat {ASC} = \frac{{AC}}{{SA}} = \frac{{a\sqrt 2 }}{{a\sqrt 6 }} = \frac{1}{{\sqrt 3 }}.\]
Dựng \[\left\{ \begin{array}{l}AE \bot BD\\AF \bot SE\end{array} \right. \Rightarrow \widehat {\left( {SA;\left( {SBD} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]
Mặt khác
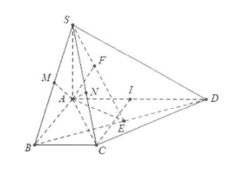
\[\begin{array}{l}AE = \frac{{AB.AD}}{{\sqrt {A{B^2} + A{D^2}} }} = \frac{{2a}}{{\sqrt 5 }}\\ \Rightarrow \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{{\sqrt {30} }}{{15}}.\end{array}\]Ví dụ 4: Cho hình chóp S.ABCD, có đáy là nửa lục giác đều cạnh a, \[AD = 2a\]. Biết \[SA \bot \left( {ABCD} \right)\] và đường thẳng SB tạo với đáy một góc 60°.
a) Tính tan góc tạo bởi SA và (SBC).
b) Tính góc tạo bởi SA và (SCD).
Lời giải
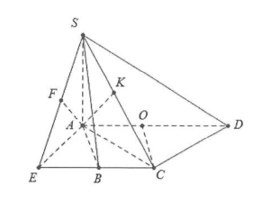
a) Gọi O là trung điểm của AD \[ \Rightarrow \] OABC là hình thoi cạnh a \[ \Rightarrow CO = a = \frac{1}{2}AD \Rightarrow \Delta ACD\] vuông tại C.
Do \[SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBA} = 60^\circ .\]
\[ \Rightarrow SA = AB\tan 60^\circ = a\sqrt 3 \], \[AC = \sqrt {A{D^2} - C{D^2}} = a\sqrt 3 .\]
Dựng \[AE \bot BC\], \[AF \bot SE\]
\[ \Rightarrow \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \widehat {ASF} = \widehat {ASE}.\]
Do \[\widehat {ABE} = 120^\circ \Rightarrow \widehat {ABE} = 60^\circ .\]
Mặt khác \[AE = AB\sin \widehat {ABE} = AB\sin 60^\circ = \frac{{a\sqrt 3 }}{2}.\]
Suy ra \[\tan \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \tan \widehat {ASE} = \frac{{AE}}{{SA}} = \frac{1}{2}.\]
b) Do \[\left\{ \begin{array}{l}CD \bot SA\\CD \bot AC\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\]
Dựng \[AK \bot SC \Rightarrow AK \bot \left( {SCD} \right)\]
Khi đó \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = \widehat {ASK} = \widehat {ASC} = \varphi .\]
Ta có: \[\tan \varphi = \frac{{AC}}{{SA}} = \frac{{a\sqrt 3 }}{{a\sqrt 3 }} = 1 \Rightarrow \varphi = 45^\circ .\]
Vậy \[\widehat {\left( {SA;\left( {SCD} \right)} \right)} = 45^\circ .\]Lời giải
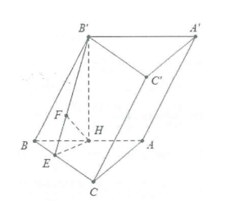
Dựng \[HE \bot BC,HF \bot B'E\] ta có:
\[\left\{ \begin{array}{l}BC \bot B'H\\BC \bot HE\end{array} \right.\] suy ra
\[\begin{array}{l}BC \bot HF \Rightarrow HF \bot \left( {B'BCC'} \right)\\ \Rightarrow \widehat {\left( {B'H;\left( {BCC'B'} \right)} \right)}\end{array}\]
\[ = \widehat {HB'F} = \widehat {HB'E}.\]
Ta có: \[HE = HB\sin \widehat {HBE} = \frac{a}{2}\sin 60^\circ = \frac{{a\sqrt 3 }}{4}\]
Do đó \[\cos \widehat {HB'E} = \frac{{B'H}}{{B'E}} = \frac{{B'H}}{{\sqrt {B'{H^2} + H{E^2}} }} = \frac{{\sqrt 3 }}{2}.\]Dạng 4: Góc giữa cạnh bên và mặt bên
Tính góc giữa cạnh bên SC và mặt phẳng (SAB). Đặt \[\widehat {\left( {SC;\left( {SAB} \right)} \right)} = \varphi \left( {0^\circ \le \varphi \le 90^\circ } \right).\]
Ta có công thức: \[\sin \varphi = \frac{{d\left( {C;\left( {SAB} \right)} \right)}}{{SC}}.\]
Từ đó suy ra các giá trị \[\cos \varphi \] hoặc \[\tan \varphi \] nếu đề bài yêu cầu.
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có \[AD = 2a,AB = a\sqrt 2 \]. Tam giác SAD cân tại S và thuộc mặt phẳng vuông góc với đáy. Đường thẳng SB tạo với đáy một góc \[30^\circ \]. Tính sin góc tạo bởi:
a) SA và mặt phẳng (SBC).
b) SD và mặt phẳng (SAC).
Lời giải
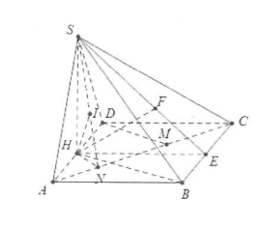
Gọi H là trung điểm của AD ta có: \[SH \bot AD\]
Lại có: \[\left( {SAD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right).\]
Ta có: \[HA = a;HB = \sqrt {H{A^2} + A{B^2}} = a\sqrt 3 \]
Do \[SH \bot \left( {ABCD} \right)\]
\[ \Rightarrow \widehat {\left( {SB;\left( {ABCD} \right)} \right)} = \widehat {SBH} = 30^\circ \]
Suy ra \[SH = HB\tan 30^\circ = a.\]
a) Do \[AD//BC \Rightarrow AD//\left( {SBC} \right).\]
Do vậy \[d\left( {A;\left( {SBC} \right)} \right) = d\left( {H;\left( {SBC} \right)} \right).\]
Dựng \[\left\{ \begin{array}{l}HE \bot BC\\HF \bot SE\end{array} \right.\] tacó: \[BC \bot HF\] từ đó suy ra \[HF \bot \left( {SBC} \right)\]
\[ \Rightarrow d\left( {H;\left( {SBC} \right)} \right) = HF = d\left( {A;\left( {SBC} \right)} \right).\]
Ta có: \[SA = \sqrt {S{H^2} + S{A^2}} = a\sqrt 2 = SD.\]
Mặt khác:
\[\begin{array}{l}\frac{1}{{H{F^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{E^2}}} \Rightarrow HF = \frac{{a\sqrt 6 }}{3}\\ \Rightarrow \sin \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{SA}} = \frac{{\sqrt 3 }}{3}.\end{array}\]
b) Dựng \[HN \bot AC \Rightarrow AC \bot \left( {SHN} \right)\]
Dựng \[HI \bot SN \Rightarrow HI \bot \left( {SAC} \right)\]
Do \[\frac{{DA}}{{HA}} = 2 = \frac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}}\]
\[ \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right) = 2HI\]
Dựng \[DM \bot AC \Rightarrow DM = \frac{{2a\sqrt 2 }}{{\sqrt 6 }} \Rightarrow HN = \frac{a}{{\sqrt 3 }}\]
\[ \Rightarrow HI = \frac{{HN.SH}}{{\sqrt {H{N^2} + S{H^2}} }} = \frac{a}{2} \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = a.\]
Ta có: \[\sin \widehat {\left( {SD;\left( {SAC} \right)} \right)} = \frac{{d\left( {D;\left( {SAC} \right)} \right)}}{{SD}} = \frac{a}{{a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}.\]Lời giải
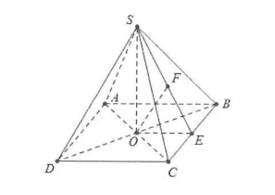
Gọi O là trung điểm của BD ta có: \[SO \bot BC\] mặt khác \[\left( {SBD} \right) \bot \left( {ABC} \right) \Rightarrow SO \bot \left( {ABC} \right)\]
Ta có: \[BD = \sqrt {A{B^2} + A{D^2}} = 2a \Rightarrow SO = \frac{1}{2}BD = a.\]
Dựng \[OE \bot BC,OF \bot SE \Rightarrow OF \bot \left( {SBC} \right).\]
\[d\left( {D;\left( {SBC} \right)} \right) = 2d\left( {O;\left( {SBC} \right)} \right) = 2HF\]
Ta có: \[HE = \frac{1}{2}AB = \frac{{a\sqrt 3 }}{2}\]
\[ \Rightarrow OF = \frac{{SH.OE}}{{\sqrt {S{H^2} + O{E^2}} }} = a\sqrt {\frac{3}{7}} = \frac{{a\sqrt {21} }}{7}\]
Suy ra \[d\left( {A;\left( {SBC} \right)} \right) = \frac{{2a\sqrt {21} }}{7}.\]
Mặt khác \[SA = \sqrt {S{O^2} + O{A^2}} = a\sqrt 2 .\]
Do đó \[\sin \widehat {\left( {SA;\left( {SBC} \right)} \right)} = \frac{{d\left( {A;\left( {SBC} \right)} \right)}}{{SA}} = \frac{{\sqrt {42} }}{7}.\]Ví dụ 3: Cho hình lăng trụ \[ABC.A'B'C'\] có đáy là tam giác vuông tại A với \[AB = a;AC = a\sqrt 3 \], hình chiếu vuông góc của \[A'\] lên mặt đáy trùng với trung điểm H của BC. Biết \[A'H = a\sqrt 2 \]. Tính cosin góc tạo bởi \[A'B\] với mặt phẳng \[\left( {ACC'A'} \right)\].
Lời giải
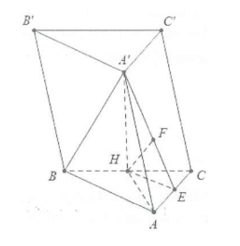
Dựng \[HE \bot AC\] và \[HF \bot A'E\]
Ta có: \[\left\{ \begin{array}{l}AC \bot A'H\\AC \bot HE\end{array} \right. \Rightarrow AC \bot HF \Rightarrow HF \bot \left( {AA'C} \right).\]
Khi đó \[d\left( {H;\left( {A'AC} \right)} \right) = HF.\]
Lại có \[BC = 2HC\] nên \[d\left( {B;\left( {AA'C} \right)} \right) = 2d\left( {H;\left( {AA'C} \right)} \right).\]
Mặt khác ME là đường trung bình trong tam giác ABC
nên \[ME = \frac{{AB}}{2} = \frac{a}{2}.\]
Khi đó: \[HF = \frac{{HE.A'M}}{{\sqrt {H{E^2} + A'{M^2}} }} = \frac{{a\sqrt 2 }}{3}\]
Suy ra \[d\left( {B;\left( {AA'C} \right)} \right) = \frac{{2a\sqrt 2 }}{3};BC = \sqrt {A{B^2} + A{C^2}} = 2a.\]
Lại có \[A'B = \sqrt {A'{H^2} + H{B^2}} = a\sqrt 3 .\]
Suy ra \[\sin \widehat {\left( {A'B;\left( {A'AC} \right)} \right)} = \sin \varphi = \frac{{d\left( {B;\left( {A'AC} \right)} \right)}}{{BA'}} = \frac{{2\sqrt 6 }}{9}\]
\[ \Rightarrow \cos \varphi = \sqrt {1 - {{\sin }^2}\varphi } = \frac{{\sqrt {57} }}{9}.\]