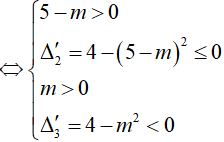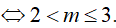Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bất phương trình logarit: Lý thuyết và các dạng bài tập, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Bất phương trình logarit: Lý thuyết và các dạng bài tập

1. Định nghĩa

Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.

2. Phương trình và bất phương trình lôgarit cơ bản: cho a,b>0,a≠1

Bất phương trình lôgarit cơ bản có dạng:  

$$\begin{gathered} {\log }_{a}f\left(x\right)>b;{\log }_{a}f\left(x\right)\ge b; \\ {\log }_{a}f\left(x\right)<b;{\log }_{a}f\left(x\right)\le b \end{gathered}$$

3. Phương pháp giải phương trình và bất phương trình lôgarit

+ Đưa về cùng cơ số

Nếu $a>1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$

$\iff \left\{\begin{array}{l}g\left(x\right)>0\\ f\left(x\right)>g\left(x\right)\end{array}\right.$

Nếu $0<a<1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$

$\iff \left\{\begin{array}{l}f\left(x\right)>0\\ f\left(x\right)<g\left(x\right)\end{array}\right.$

+ Đặt ẩn phụ

+ Mũ hóa

+ Phương pháp hàm số và đánh giá

4. Các dạng bài tập và phương pháp giải

Dạng 1. Bất phương trình logarit cơ bản

A. Phương pháp giải

Ta có BPT

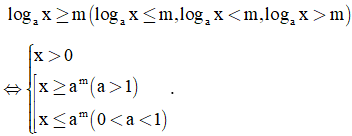
B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình ${\log }_3\left({\log }_{\frac{1}{2}}x\right)<1$ là:

A. $\left(0;1\right).$

B. $\left(\frac{1}{8};1\right).$

C. $\left(1;8\right).$

D. $\left(\frac{1}{8};3\right).$

Hướng dẫn giải

$$\begin{gathered} {\log }_3\left({\log }_{\frac{1}{2}}x\right)<1\iff 0<{\log }_{\frac{1}{2}}x<3 \\ \iff 1>x>{\left(\frac{1}{2}\right)}^3\iff \frac{1}{8}<x<1 \end{gathered}$$

Vậy tập nghiệm của BPT $\left(\frac{1}{8};1\right).$

Chọn B.

Câu 2: Bất phương trình ${\log }_2\left(x^2-2x+3\right)>1$ có tập nghiệm là

A. $ℝ\backslash \left\{1\right\}$

B. $ℝ$

C. $\left\{1\right\}$

D. $\varnothing$

Hướng dẫn giải

Chọn A.

$$\begin{gathered} {\log }_2\left(x^2-2x+3\right)>1 \\ \iff x^2-2x+3>2^1 \\ \iff x^2-2x+1>0 \\ \iff {\left(x-1\right)}^2>0\iff x\ne 1 \end{gathered}$$

Vậy tập nghiệm $S=ℝ\backslash \left\{1\right\}$

Câu 3: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left(2x-1\right)>-1$ là:

A. $\left(1;\frac{3}{2}\right)$

B. $\left(\frac{3}{2};+\infty \right)$

C. $\left(\frac{1}{2};\frac{3}{2}\right)$

D. $\left(-\infty ;\frac{3}{2}\right)$

Hướng dẫn giải

Chọn C.

Ta có:

$$\begin{gathered} {\log }_{\frac{1}{2}}\left(2x-1\right)>-1 \\ \iff \left\{\begin{array}{c}2x-1<2\\ 2x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{c}x<\frac{3}{2}\\ x>\frac{1}{2}\end{array}\right.\iff \frac{1}{2}<x<\frac{3}{2}. \end{gathered}$$

Vậy tập nghiệm của BPT là: $S=\left(\frac{1}{2};\frac{3}{2}\right)$

Câu 4: Điều kiện xác định của bất phương trình $\ln \frac{x^2-1}{x}<0$ là:

A. $\left[\begin{array}{l}-1<x<0\\ x>1\end{array}\right.$

B. $x>-1$

C. $x>0$

D. $\left[\begin{array}{l}x<-1\\ x>1\end{array}\right.$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện:

$\frac{x^2-1}{x}>0\iff \left[\begin{array}{l}-1<x<0\\ x>1\end{array}\right.$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính $\ln \frac{X^2-1}{X}$

Nhấn CALC và cho $X=-0,5$ (thuộc đáp án A và B) máy tính hiển thị 0,4054651081. Vậy loại đáp án C và  D.

Nhấn CALC và cho $X=0,5$(thuộc đáp án B) máy tính không tính được. Vậy loại B,

Chọn A.

Câu 5: Bất phương trình ${\log }_{\frac{2}{3}}\left(2x^2-x+1\right)<0$ có tập nghiệm là:

A. $S=\left(0;\frac{3}{2}\right)$

B. $S=\left(-1;\frac{3}{2}\right)$

C. $S=\left(-\infty ;0\right)\cup \left(\frac{1}{2};+\infty \right)$

D. $S=\left(-\infty ;1\right)\cup \left(\frac{3}{2};+\infty \right)$

Hướng dẫn giải

[Phương pháp tự luận]

$$\begin{gathered} {\log }_{\frac{2}{3}}\left(2x^2-x+1\right)<0 \\ \iff 2x^2-x+1>1\iff \left[\begin{array}{l}x<0\\ x>\frac{1}{2}\end{array}\right. \end{gathered}$$

Vậy tập nghiệm của BPT $S=\left(-\infty ;0\right)\cup \left(\frac{1}{2};+\infty \right)$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính ${\log }_{\frac{2}{3}}\left(2X^2-X+1\right)$

Nhấn CALC và cho $X=-5$ (thuộc đáp án A và D) máy tính hiển thị – 9,9277….

Vậy loại đáp án A và B.

Nhấn CALC và cho $X=1$ (thuộc đáp án C) máy tính hiển thị – 1,709511291.

Chọn C.

Câu 6: Tập nghiệm của bất phương trình ${\log }_3\frac{4x+6}{x}\le 0$ là:

A. $S=\left[-2;-\frac{3}{2}\right)$

B. $S=\left[-2;0\right)$

C. $S=\left(-\infty ;2\right]$

D. $S=ℝ\backslash \left[-\frac{3}{2};0\right]$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

$$\begin{gathered} {\log }_3\frac{4\text{x}+6}{x}\le 0\iff \left\{\begin{array}{l}\frac{4\text{x}+6}{x}>0\\ \frac{4\text{x}+6}{x}\le 1\end{array}\right. \\ \iff \left\{\begin{array}{l}x<-\frac{3}{2}\vee x>0\\ -2\le x<0\end{array}\right. \\ \iff -2\le x<-\frac{3}{2} \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left[-2;-\frac{3}{2}\right)$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính ${\log }_3\frac{4X+6}{X}$

Nhấn CALC và cho $X=1$ (thuộc đáp án C và D) máy tính hiển thị 2,095903274. Vậy loại đáp án C và D.

Nhấn CALC và cho $X=-1$ (thuộc đáp án B) máy tính không tính được. Vậy loại B

Dạng 2. Phương pháp đưa về cùng cơ số

A. Phương pháp giải

Xét bất phương trình ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$ $(a>0,a\ne 1)$

Nếu $a>1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)>g\left(x\right)$ (cùng chiều khi a > 1)

Nếu $0<a<1$ thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff f\left(x\right)<g\left(x\right)$ (ngược chiều khi $0<a<1$)

Nếu a chứa ẩn thì ${\log }_{a}f\left(x\right)>{\log }_{a}g\left(x\right)$$\iff \left\{\begin{array}{l}f\left(x\right)>0;g\left(x\right)>0\\ (a-1)\left[f\left(x\right)-g\left(x\right)\right]>0\end{array}\right.$(hoặc chia 2 trường hợp của cơ số)

B. Ví dụ minh họa

Câu 1: Điều kiện xác định của bất phương trình ${\log }_{\frac{1}{2}}(4x+2)-{\log }_{\frac{1}{2}}(x-1)>lo{g}_{\frac{1}{2}}x$ là:

A. $x>-\frac{1}{2}$

B. $x>0$

C. $x>1$

D. $x>-1$

Hướng dẫn giải

Chọn C.

BPT xác định khi:

$$\begin{gathered} \left\{\begin{array}{l}x>0\\ 4x+2>0\\ x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>0\\ x>-\frac{1}{2}\\ x>1\end{array}\right.\iff x>1 \end{gathered}$$

Câu 2: Điều kiện xác định của bất phương trình ${\log }_2(x+1)-2{\log }_4(5-x)<1-{\log }_2(x-2)$ là:

A. $2<x<5$

B. $1<x<2$

C. $2<x<3$

D. $-4<x<3$

Hướng dẫn giải

Chọn A.

BPT xác định khi:

$$\begin{gathered} \left\{\begin{array}{l}x+1>0\\ 5-x>0\\ x-2>0\end{array}\right.\iff \left\{\begin{array}{l}x>-1\\ x<5\\ x>2\end{array}\right. \\ \iff 2<x<5 \end{gathered}$$

Câu 3: Điều kiện xác định của bất phương trình ${\log }_5(x-2)+{\log }_{\frac{1}{5}}(x+2)>{\log }_{5}x-3$ là:

A. $x>3$

B. $x>2$

C. $x>-2$

D. $x>0$

Hướng dẫn giải

Chọn B.

[Phương pháp tự luận]

Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}x-2>0\\ x+2>0\\ x>0\end{array}\right.\iff \left\{\begin{array}{l}x>2\\ x>-2\\ x>0\end{array}\right. \\ \iff x>2 \end{gathered}$$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_5(X-2)+{\log }_{\frac{1}{5}}(X+2)-{\log }_{5}X+3$

Nhấn CALC và cho $X=1$ máy tính không tính được. Vậy loại đáp án C và D.

Nhấn CALC và cho $X=\frac{5}{2}$(thuộc đáp án B) máy tính hiển thị 1,065464369.

Câu 4: Điều kiện xác định của bất phương trình ${\log }_{0,5}(5\text{x}+15)\le {\log }_{0,5}\left(x^2+6\text{x}+8\right)$ là:

A. $x>-2$

B. $\left[\begin{array}{l}x<-4\\ x>-2\end{array}\right.$

C. $x>-3$

D. $-4<x<-2$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện:

$$\begin{gathered} \left\{\begin{array}{l}5x+15>0\\ x^2+6\text{x}+8>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>-3\\ \left[\begin{array}{l}x>-2\\ x<-4\end{array}\right.\end{array}\right. \\ \iff x>-2 \end{gathered}$$

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{0,5}(5X+15)-{\log }_{0,5}(X^2+6\text{X}+8)$

Nhấn CALC và cho $X=-3,5$ máy tính không tính được. Vậy loại đáp án C và  D.

Nhấn CALC và cho $X=-5$ (thuộc đáp án B) máy tính không tính được.

Vậy loại B,

Chọn A.

Câu 5: Tập nghiệm của bất phương trình ${\log }_{\frac{1}{3}}\left(x^2-6x+5\right)+{\log }_3\left(x-1\right)\ge 0$ là:

A. $S=\left[1;6\right]$

B. $S=\left(5;6\right]$

C. $S=\left(5;+\infty \right)$

D. $S=\left(1;+\infty \right)$

Hướng dẫn giải

[Phương pháp tự luận]

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{\frac{1}{3}}\left(X^2-6\text{X}+5\right)+{\log }_3\left(X-1\right)$

Nhấn CALC và cho $X=2$ (thuộc đáp án A và D) máy tính không tính được. Vậy loại đáp án A và D.

Nhấn CALC và cho $X=7$ (thuộc đáp án C) máy tính hiển thị – 0,6309297536.

Vậy loại C,

Chọn B.

Câu 6: Nghiệm nguyên nhỏ nhất của bất phương trình ${\log }_{0,2}x-{\log }_5\left(x-2\right)<{\log }_{0,2}3$ là:

A. $x=6$

B. $x=3$

C. $x=5$

D. $x=4$

Hướng dẫn giải

[Phương pháp tự luận]

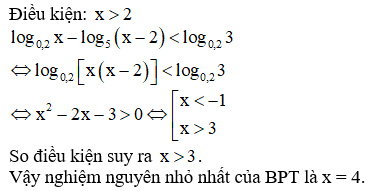
[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_{0,2}X-{\log }_5\left(X-2\right)-{\log }_{0,2}3$

Nhấn CALC và cho $X=3$  (nhỏ nhất) máy tính hiển thị 0. Vậy loại đáp án B.

Nhấn CALC và cho $X=4$ máy tính hiển thị -0.6094234797.

Chọn D.

Dạng 3. Phương pháp đặt ẩn phụ

A. Phương pháp giải

Tương tự với phương pháp giải phương trình logarit bằng phương pháp đặt ẩn phụ nhưng lưu ý tới chiều biến thiên của hàm số.

B. Ví dụ minh họa

Câu 1 : Nghiệm nguyên lớn nhất của bất phương trình ${\log }_2^{4}x-{\log }_{\frac{1}{2}}^2\left(\frac{x^3}{8}\right)+9{\log }_2\left(\frac{32}{x^2}\right)<4{\log }_{2^{-1}}^2\left(x\right)$ là:

A. $x=7$

B. $x=8$

C. $x=4$

D. $x=1$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

Điều kiện: x >0

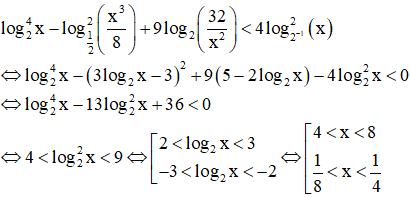
Vậy giá trị nguyên lớn nhất của x thỏa mãn ĐK trên là: x = 7.

[Phương pháp trắc nghiệm]

Lần lượt thay $x=7;x=8;x=4;x=1$ thấy $x=7$ đúng.

Câu 2: Bất phương trình ${\log }_{0,2}^{2}x-5{\log }_{0,2}x<-6$ có tập nghiệm là:

A. $S=\left(\frac{1}{125};\frac{1}{25}\right)$

B. $S=\left(2;3\right)$

C. $S=\left(0;\frac{1}{25}\right)$

D. $S=\left(0;3\right)$

Hướng dẫn giải

Chọn A.

[Phương pháp tự luận]

Điều kiện: $x>0$

$$\begin{gathered} {\log }_{0,2}^2-5{\log }_{0,2}x<-6 \\ \iff 2<{\log }_{0,2}x<3 \\ \iff \frac{1}{125}<x<\frac{1}{25} \end{gathered}$$

Vậy tập nghiệm của BPT là $S=\left(\frac{1}{125};\frac{1}{25}\right)$.

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\left({\log }_{0,2}^{}X\right)}^2-5{\log }_{0,2}X+6$

Nhấn CALC và cho $X=2,5$ (thuộc đáp án B và D) máy tính hiển thị 9.170746391. Vậy loại đáp án B và D.

Nhấn CALC và cho $X=\frac{1}{200}$ (thuộc đáp án C) máy tính hiển thị 0,3773110048.

Câu 3: Nghiệm nguyên nhỏ nhất của bất phương trình ${\log }_{x}3-{\log }_{\frac{x}{3}}3<0$ là:

A. x = 3

B. x =1

C. x =2

D. x =4

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện: $x>0;x\ne 1;x\ne 3$

$$\begin{gathered} {\log }_{x}3-{\log }_{\frac{x}{3}}3<0 \\ \iff \frac{-1}{{\log }_{3}x.\left({\log }_{3}x-1\right)}<0 \\ \iff \left[\begin{array}{l}{\log }_{3}x<0\\ {\log }_{3}x>1\end{array}\right.\iff \left[\begin{array}{l}0<x<1\\ x>3\end{array}\right. \end{gathered}$$

Vậy nghiệm nguyên nhỏ nhất của BPT là x = 4.

[Phương pháp trắc nghiệm]

Loại B, A vì $x\ne 1;x\ne 3$

Loại C vì $x=2\Rightarrow {\log }_{2}3-{\log }_{\frac{2}{3}}3>0$

Chọn D.

Câu 4: Nếu đặt $t={\log }_3\frac{x-1}{x+1}$ thì bất phương trình ${\log }_4{\log }_3\frac{x-1}{x+1}<{\log }_{\frac{1}{4}}{\log }_{\frac{1}{3}}\frac{x+1}{x-1}$ trở thành bất phương trình nào?

A. $\frac{t^2-1}{t}<0$

B. $t^2-1<0$

C. $\frac{t^2-1}{t}>0$

D. $\frac{t^2+1}{t}<0$

Hướng dẫn giải

Điều kiện: $x\in (-\infty ;-1)\cup (1;+\infty )$

Sau khi đưa về cùng cơ số 4, rồi tiếp tục biến đổi về cùng cơ số 3 ta được bất phương trình

${\log }_3\frac{x-1}{x+1}-\frac{1}{{\log }_3\frac{x-1}{x+1}}<0$

Chọn A.

Dạng 4. Phương pháp mũ hóa

A. Phương pháp giải

Tương tự với giải phương trình logarit bằng phương pháp mũ hóa.

B. Ví dụ minh họa

Câu 1: Bất phương trình ${\log }_x\left({\log }_3\left(9^x-72\right)\right)\le 1$ có tập nghiệm là:

A. $S=\left[{\log }_3\sqrt{73};2\right]$

B. $S=\left({\log }_3\sqrt{72};2\right]$

C. $S=\left({\log }_3\sqrt{73};2\right]$

D. $S=\left(-\infty ;2\right]$

Hướng dẫn giải

[Phương pháp tự luận]

Điều kiện $x>{\log }_3\sqrt{73}$

$$\begin{gathered} {\log }_x\left({\log }_3\left(9^x-72\right)\right)\le 1 \\ \iff {\log }_3\left(9^x-72\right)\le x \\ \iff 9^x-3^x-72\le 0 \\ \iff 3^x\le 9\iff x\le 2 \end{gathered}$$

Kết hợp với điều kiện ${\log }_3\sqrt{73}<x\le 2$

Vậy tập nghiệm của BPT là: $S=\left({\log }_3\sqrt{73};2\right]$

Chọn A.

[Phương pháp trắc nghiệm]

Thay $x={\log }_3\sqrt{73}$ (thuộc B, C, D) vào biểu thức ${\log }_x\left({\log }_3\left(9^x-72\right)\right)$ được ${\log }_x\left(0\right)$ không xác định, vậy loại B, C, D.

 Chọn A.

Câu 2: Điều kiện xác định của phương trình ${\log }_2\left[3{\log }_2\left(3x-1\right)-1\right]=x$ là:

A. $x>\frac{\sqrt[3]{2}+1}{3}$

B.  $x\ge \frac{1}{3}$

C. $x>0$

D. $x\in (0;+\infty )\backslash \text{{}1\}$

Hướng dẫn giải

[Phương pháp tự luận]

Biểu thức ${\log }_2\left[3{\log }_2\left(3x-1\right)-1\right]=x$ xác định khi và chỉ khi:

$$\begin{gathered} \left\{\begin{array}{l}3{\log }_2\left(3x-1\right)-1>0\\ 3x-1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}{\log }_2\left(3x-1\right)>\frac{1}{3}\\ x>\frac{1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}3x-1>2^{\frac{1}{3}}\\ x>\frac{1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x>\frac{2^{\frac{1}{3}}+1}{3}\\ x>\frac{1}{3}\end{array}\right. \\ \iff x>\frac{2^{\frac{1}{3}}+1}{3} \end{gathered}$$

[Phương pháp trắc nghiệm]

Thay $x=\frac{1}{3}$ (thuộc B, C, D) vào biểu thức ${\log }_2\left(3x-1\right)$ được ${\log }_2\left(0\right)$ không xác định, vậy loại B, C, D.

Chọn A.

Câu 3: Nghiệm nguyên lớn nhất của bất phương trình ${\log }_3\left({4.3}^{x-1}\right)>2x-1$ là:

A. $x=3$

B. $x=2$

C. $x=1$

D. $x=-1$

Hướng dẫn giải

[Phương pháp tự luận]

$$\begin{gathered} {\log }_3\left({4.3}^{x-1}\right)>2x-1 \\ \iff {4.3}^{x-1}>3^{2x-1} \\ \iff 3^{2x}-{4.3}^x<0 \\ \iff 0<3^x<4\iff x<{\log }_{3}4 \end{gathered}$$

Vậy nghiệm nguyên lớn nhất của BPT là: x = 1.

[Phương pháp trắc nghiệm]

Nhập vào màn hình máy tính:

${\log }_3\left({4.3}^{X-1}\right)-2X+1$

Nhấn CALC và cho $X=3$ (lớn nhất) máy tính hiển thị –1.738140493. Vậy loại đáp án    A.

Nhấn CALC và cho $X=2$ máy tính hiển thị – 0.7381404929. Vậy loại B.

Nhấn CALC và cho $X=1$ máy tính hiển thị 0.2618595071.

Chọn C.

Dạng 5. Phương pháp hàm số, đánh giá

A. Phương pháp giải

Cho hàm số $y=f\left(t\right)$ xác định và liên tục trên D:

Nếu hàm số $f\left(t\right)$ luôn đồng biến trên D và $\forall u,v\in D$ thì $f\left(u\right)>f\left(v\right)\iff u>v$

Nếu hàm số $f\left(t\right)$ luôn nghịch biến trên D và $\forall u,v\in D$ thì $f\left(u\right)>f\left(v\right)\iff u<v$

B. Ví dụ minh họa

Câu 1: Tập nghiệm của bất phương trình ${\log }_2\left(x^2-4x+16\right)-{\log }_2\left(x\right)\le -5x^2+40x-74$ là:

A. $\left(-4;4\right)$

B. $\left(4;+\infty \right)$

C. $\left\{4\right\}$

D. $\left(-\infty ;4\right)$

Hướng dẫn giải

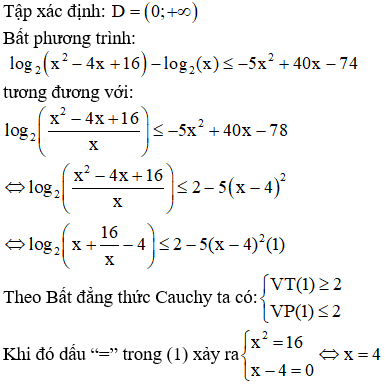
So với điều kiện xác định ta nhận nghiệm x= 4

So bốn đáp án, chỉ có đáp án C thỏa mãn.

Chọn C.

Câu 2: Cho bất phương trình ${\log }_2\left(\frac{x^2+2x+3}{x^2+3x+2}\right)\le -2x+2$. Phát biểu nào sau đây là Sai:

A. Bất phương trình đã cho có tập nghiệm là $T=\left(-\infty ;-2\right)\cup \left(\left.-1;1\right]\right.$

B. Bất phương trình đã cho có tập nghiệm là $T=\left(-\infty ;0\right)\cup \left(1;+\infty \right)$

C. Tập xác định của phương trình đã cho là $\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

D. Bất phương trình đã cho không có nghiệm nguyên.

Hướng dẫn giải

Bất phương trình :

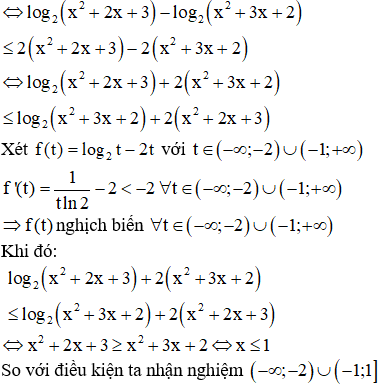
Chọn B.

Câu 3: Bất phương trình ${\log }_2(2^x+1)+{\log }_3(4^x+2)\le 2$ có tập nghiệm là:

A. $\text{[}0;+\infty )$

B. $(-\infty ;0)$

C. $(-\infty ;0]$

D. $\left(0;+\infty \right)$

Hướng dẫn giải

Chọn C.

Xét:

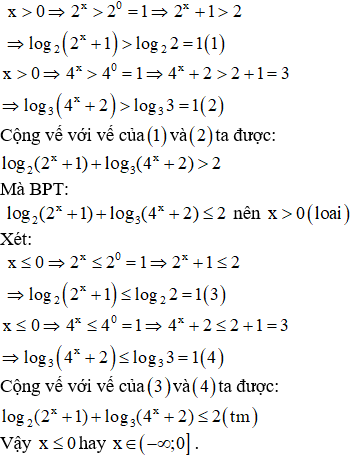
5. Bài tập vận dụng

Bài 1. Điều kiện xác định của bất phương trình 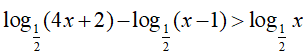 là

 

Hướng dẫn giải

Đáp án: C

Bất phương trình xác định khi:

 

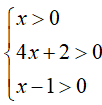
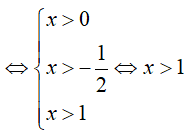
Bài 2. Điều kiện xác định của bất phương trình 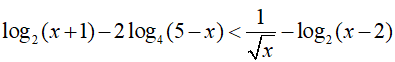 là

A. 2 < x < 5

B. 1 < x < 2.

C. 2 < x < 3

D. −4 < x < 3

Hướng dẫn giải

Đáp án: A

Bất phương trình xác định khi:

 

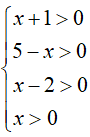
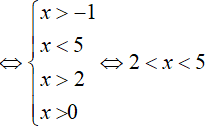
Bài 3. Điều kiện xác định của bất phương trình 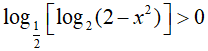 là

A. x ∈ [−1; 1] .

B. x ∈ (−1; 0) ∪ (0; 1) .

C. x ∈ (−1; 1) ∪ (2; +∞).

D. x ∈ (−1; 1).

Hướng dẫn giải

Đáp án: D

Bất phương trình xác định khi:

   

 

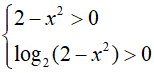
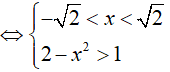
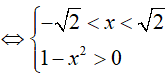
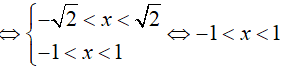
Bài 4. Giải bất phương trình: log₅ (x − 2) + 2log₂₅ x > log₅3.

 

Hướng dẫn giải

Đáp án: C

Điều kiện:

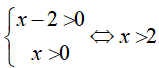
Với điều kiện trên, bất phương trình trở thành:

log₅ (x − 2) + log₅x > log₅3

⇔ log₅ ( x − 2).x > log₅3 ⇔ (x − 2).x > 3

⇔ x² − 2x − 3 > 0

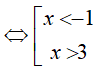
Kết hợp với điều kiện ta được, x > 3

Bài 5. Nghiệm nguyên nhỏ nhất của bất phương trình log₂(log₄x) ≥ log₄(log₂x) là:

A. 6.    B. 10.    C. 8.    D. 16.

Hướng dẫn giải

Đáp án: D

BPT

       

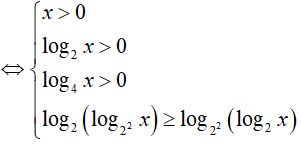
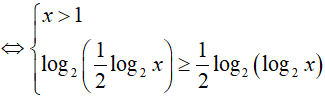
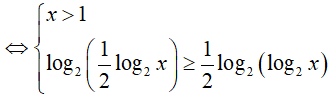
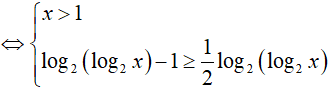
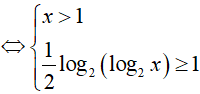
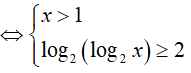
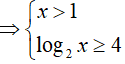
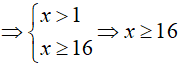
Bài 6. Nghiệm nguyên nhỏ nhất của bất phương trình 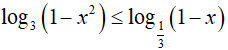 là:

 

Hướng dẫn giải

Đáp án: A

BPT

       

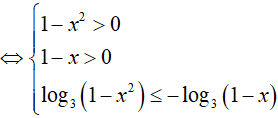
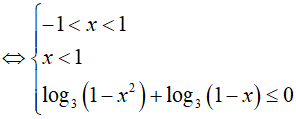
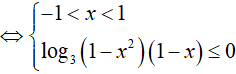
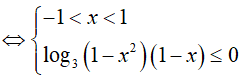
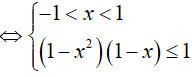
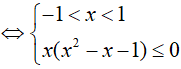
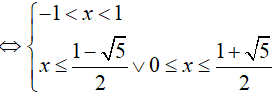
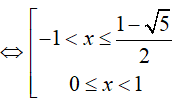
Do đó, x = 0 là nghiệm nguyên nhỏ nhất.

Bài 7. Bất phương trình log_0,2²x − 5log_0,2x < −6 có tập nghiệm là:

 

Hướng dẫn giải

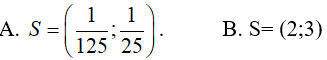
Đáp án: A

Điều kiện: x > 0

Đặt t = log_0,2x. Khi đó, bất phương trình đã cho trở thành:

t² − 5t < − 6 ⇔ t² − 5t + 6 < 0 hay 2 < t < 3.

Khi đó, ta có: 2 < log_0,2x < 3 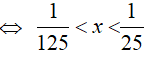( thỏa mãn điều kiện).

Bài 8. Giải bất phương trình log₃(4 . 3^{x − 1}) > 2x − 1 :

 

Hướng dẫn giải

Đáp án: A

Bất phương trình đã cho luôn xác định với mọi x.

Ta có: log₃ (4. 3^x−1) > 2x − 1

⇔ 4.3^{x − 1} > 3^{2x − 1} ⇔ 3^2x − 4. 3^x < 0 (*)

Đặt t = 3^x ( t > 0). Khi đó, phương trình (*) trở thành:

t² − 4t < 0 ⇔ 0 < t < 4

suy ra, 0 < 3^x < 4 ⇔ x < log₃4

Bài 9. Nếu đặt t =log2x thì bất phương trình 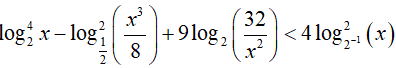 trở thành bất phương trình nào?

A. t⁴ +13t² + 36 < 0 .    B. t⁴ + 12t² + 12 < 0

C. t⁴ < 24t² + 23 > 0    D. t⁴ − 13t² + 36 < 0

Hướng dẫn giải

Đáp án: D

Điều kiện: x > 0.

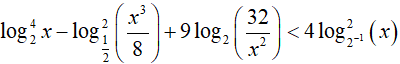
⇔ log₂⁴x − (−log₂x³ + log₂8)² + 9(log₂32 − log₂x²) < 4log₂²x

⇔ log₂⁴x − (3log₂x − 3)² + 9(5 − 2log₂x) − 4log₂²x < 0

⇔ log₂⁴x − (9log₂²x − 18log₂x + 9) + 45 − 18log₂x − 4log₂² < 0

⇔ log₂⁴x − 13log₂²x + 36 < 0

Đặt t= log₂x khi đó phương trình trên trở thành :

t⁴ − 13t² + 36 < 0

Bài 10. Bất phương trình log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 có tập nghiệm là:

A. [0; +∞).    B. (−∞; 0).    C. (−∞; 0].    D. (0; +∞) .

Hướng dẫn giải

Đáp án: C

* Xét x > 0 => 2^x > 2⁰ = 1 => 2^x + 1 > 2

Suy ra, log₂ (2^x +1) > log₂2 = 1 (1)

* Khi x > 0 thì 4^x > 4⁰ = 1 => 4^x + 2 > 2 + 1= 3

Suy ra, log₃ (4^x + 2) > log₃3 = 1 ( 2)

* Cộng vế với vế của (1) và (2) ta được: log₂ (2^x + 1) + log₃ ( 4^x + 2) > 2

Mà BPT: log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 nên x > 0 ( loại) .

* Xét x ≤ 0

    

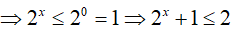
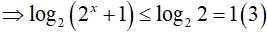
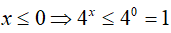
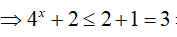
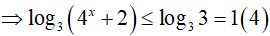
Cộng vế với vế của (3) và (4) ta được: log₂(2^x + 1) + log₃(4^x + 2) ≤ 2 (tm)

Vậy x ≤ 0 hay x ∈ (−∞; 0]

Bài 11. Giải bất phương trình: log₃ (2^x + 1) + x ≤ 2

 

Hướng dẫn giải

Đáp án: B

Điều kiện:

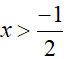
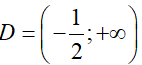
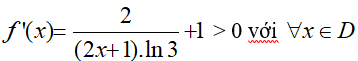
Xét hàm số y = f(x) = log₃(2^x + 1) + x trên  có đạo hàm:

Suy ra, hàm số đồng biến trên 

Khi đó, log₃ (2^x + 1) + x ≤ 2 ⇔ f(x) ≤ f(1) ⇔ x ≤ 1

Kết hợp với điều kiện , ta có nghiệm của bất phương trình đã cho là 

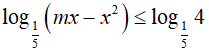
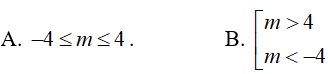
Bài 12. Tìm tất cả giá trị thực của tham số m để bất phương trình  vô nghiệm?

 

Hướng dẫn giải

Đáp án: D

 

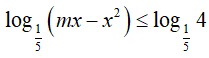
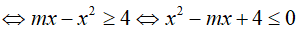
Để bất phương trình đã cho vô nghiệm khi và chỉ khi bất phương trình: x² − mx + 4 ≤ 0 vô nghiệm

⇔ x² − mx + 4 > 0 ∀x ∈ R ⇔ Δ = m² − 16 < 0 ⇔ −4 < m < 4

Bài 13. Tìm tất cả các giá trị thực của tham số m để bất phương trình log₂(5^x − 1). log₂(2.5^x − 2) ≥ m có nghiệm x ≥ 1 ?

A. m ≥ 6.    B. m > 6    C. m ≤ 6.    D. m < 6

Hướng dẫn giải

Đáp án: C

BPT

 

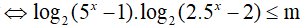
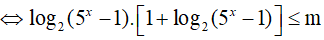
Đặt 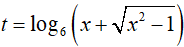 do x ≥ 1 => t ∈ [2; +∞)

BPT

 

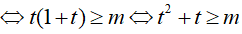
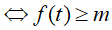
Với f(t) = t² + t có f’(t) = 2t + 1 > 0 với t ∈ [2; +∞) nên hàm đồng biến trên t ∈ [2; +∞)

Nên min f(t) = f(2) = 6.

Do đó để để bất phương trình log₂(5^x − 1). log₂(2.5^x − 2) ≥ m có nghiệm x ≥ 1 thì :

m ≤ Minf(t) ⇔ m < 6

Bài 14. Tìm tất cả các giá trị thực của tham số m sao cho khoảng (2 ; 3) thuộc tập nghiệm của bất phương trình log₅ (x² + 1) > log₅ (x² +4x + m) − 1.

 

Hướng dẫn giải

Đáp án: A

Ta có: log₅ (x² + 1) > log₅ (x² +4x + m) − 1

   

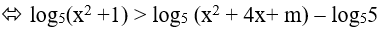
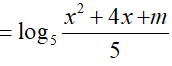
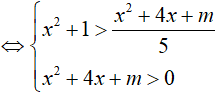
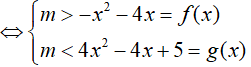
Hệ trên thỏa mãn ∀x ∈ (2; 3)

 

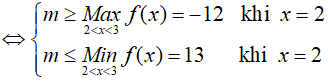
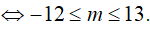
Bài 15. Tìm tất cả các giá trị thực của tham số m để bất phương trình log₂(7x² + 7) ≥ log₂(mx² + 4x + m), ∀x ∈ R

 

Hướng dẫn giải

Đáp án: C

Bất phương trình tương đương : 7x² + 7 ≥ mx² + 4x + m > 0, ∀x ∈ R

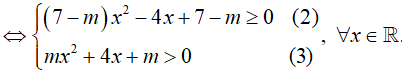
Nếu m = 7 thì (2) không thỏa ∀x ∈ R

Nếu m =0 thì (3) không thỏa ∀x ∈ R

Do đó, để (1) thỏa ∀x ∈ R

  

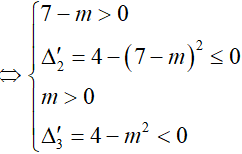
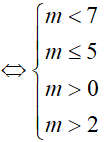
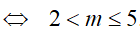
Bài 16. Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log₅(x² + 1) ≥ log₅(mx² + 4x + m) có nghiệm đúng mọi x.

 

Hướng dẫn giải

Đáp án: A

Bất phương trình tương đương : 5(x² + 1) ≥ mx² + 4x + m > 0, ∀x ∈ R

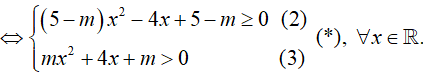
Nếu m = 0 hoặc m= 5 : (*) không thỏa ∀x ∈ R

m ≠ 0 và m ≠ 5: (*)