Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Dạng toán tính nhanh lớp 5 và bài tập vận dụng chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết về phương pháp tính nhanh, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Dạng toán tính nhanh lớp 5 và bài tập vận dụng

I. Kiến thức cần nhớ tính nhanh

1. Phép cộng

1.1. Tính chất giao hoán: Tổng không thay đổi khi ta đổi chỗ các số hạng.

Tổng quát: a + b + c + d = a + c + b + d = b + c + d + a = …

1.2. Tính chất kết hợp: Tổng không thay đổi, khi ta thay hai hay nhiều số hạng của tổng bằng tổng của chúng.

Tổng quát: a + b + c + d = a + (b + c) + d = a + b +(c + d) = …..

1.3. Tổng không thay đổi, khi ta thêm số hạng này bao nhiêu đơn vị và bớt đi số hạng kia bấy nhiêu đơn vị.

Tổng quát: a + b = (a - n) + (b + n) = (a + n) + (b - n)

2. Phép trừ

2.1. Hiệu hai số không thay đổi, nếu ta cùng thêm (hoặc cùng bớt) ở hai số cùng một số như nhau.

Tổng quát: a - b = (a - n ) - (b - n) = (a + n) - (b + n)

2.2. Trong phép trừ thì:

Số bị trừ = số trừ + hiệu số.

Số trừ = số bị trừ - hiệu số.

Hiệu số = số bị trừ - số trừ.

3. Phép nhân

3.1. Tổng các số hạng bằng nhau, có thể chuyển thành phép nhân, trong đó một thừa số là một số hạng còn thừa số thứ hai bằng số lượng số hạng của tổng.

Tổng quát: a + a + a +...+ a + a = a n ( Có n số hạng là a)

3.2. Tính chất giao hoán: Tích không thay đổi, khi ta đổi cổ các thừa số.

Tổng quát: a x b x c x d = a x c x b x d = b x d x a x c = ...

3.3. Tính chất kết hợp: Tích của chúng không đổi, khi ta thay hai hay nhiều thừa số bằng tích riêng của chúng.

Tổng quát: a × b × c × d = (a × b) (c × d) = (a × c) × (b × d) = (a × d) × (b × c)

3.4. Muốn nhân một số với 0,5 ta chỉ cần chia số đó cho 2.

Tổng quát: a × 0,5 = a : 2

3.5. Muốn nhân một số với 0,25 ta chỉ cần chia số đó cho 4.

Tổng quát: a × 0,25 = a : 4

3.6. Muốn nhân một số với 0,2 ta chỉ cần chia số đó cho 5.

Tổng quát: a × 0,2 = a : 5

3.7. Muốn nhân một số với 0,125 ta chỉ cần chia số đó cho 8.

Tổng quát: a × 0,125 = a : 8

3.8. Muốn nhân một số với 0,05 ta chỉ cần chia số đó cho 20.

Tổng quát: a × 0,05 = a : 20

3.9. Muốn nhân một số với 0,025 ta chỉ cần chia số đó cho 40.

Tổng quát: a × 0,025 = a : 40

3.10. Muốn nhân một số với 0,02 ta chỉ cần chia số đó cho 50.

Tổng quát: a × 0,02 = a : 50

3.11. Muốn nhân một số với 0,0125 ta chỉ cần chia số đó cho 80.

Tổng quát: a × 0,0125 = a : 80

3.12. Muốn nhân một số với 0,1 ; 0,01 ; 0,001.. ta chỉ cần chia số đó cho 10 ; 100 ; 1000 .

Tổng quát: a × 0.1 = a : 10; a × 0.01 = a : 100;

a × 0.001 = a : 1000; a × 0.001 = a : 1000

3.13. Tích của hai thừa số không đổi khi ta tăng thừa số này lên bao nhiêu lần, thì giảm thừa số kia đi bấy nhiêu lần.

Tổng quát: a × b = (a × n) × ( b : n) = (a : n) × (b x n)

3.14. Tích bằng 0 khi có một thừa số bằng 0.

Tổng quát: a × b × c × d = 0 khi chỉ cần a, hoặc b, hoặc c hoặc, d bằng 0

4. Phép chia

4.1. Trong phép chia thì:

* Số bị chia = số chia số thương.

* Số chia = số bị chia : số thương.

* Số thương = số bị chia : số chia.

4.2. Trong phép chia, nếu ta cùng tăng (hoặc cùng giảm) cả số bị chia và số chia đi cùng một số lần thi thương không thay đổi.

Tổng quát: a : b = (a x n) : (b x n) = (a : n) : (b : n)

4.3. Muốn chia một số cho 0,5, ta có thể nhân số đó với 2.

Tổng quát: a : 0,5 = a x 2

....

II. Các bài toán Tính giá trị của biểu thức

1. PHƯƠNG PHÁP CHUNG

+ Nhóm các số hạng trong biểu thức thành từng nhóm có tổng (hoặc hiệu) là các số tròn chục, tròn trăm, tròn nghìn,....rồi cộng (trừ) các kết quả lại.

+ Vận dụng tính chất: một số nhân với một tổng, một số nhân với một hiệu, một tổng chia cho một số...

+ Vận dụng tính chất của các phép tính để tính giá trị của biểu thức bằng cách thuận tiện nhất

+ Vận dụng một số kiến thức về dãy số để tính giá trị của biểu thức theo cách thuận tiện nhất

2. CÁC DẠNG TOÁN

Dạng 1. Tính giá trị biểu thức số tự nhiên

Ví dụ 1. Tính giá trị của biểu thức: 

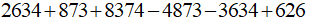
Giải

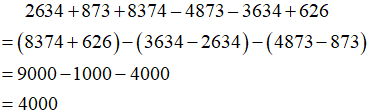
Ví dụ 2. Tính giá trị của biểu thức:

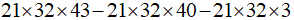
Giải

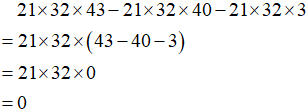
Dạng 2. Tính giá trị biểu thức với phân số

Ví dụ 1. Tính:

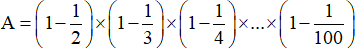
Bài giải

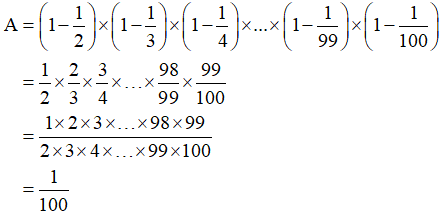
Vậy .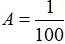

Ví dụ 2. Tính:

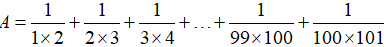
Bài giải

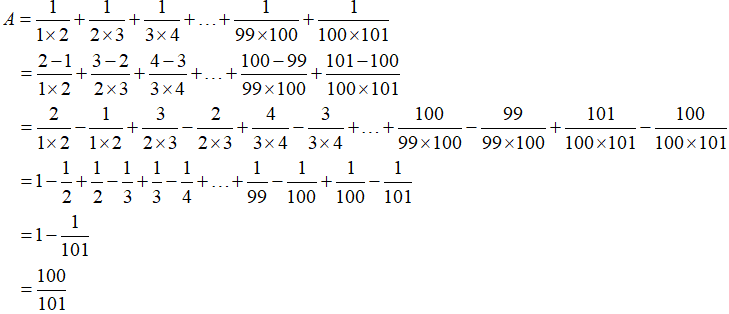
Dạng 3. Tính giá trị biểu thức với số thập phân

Ví dụ 1. Tính giá trị biểu thức sau: 

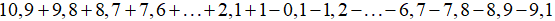
Bài giải

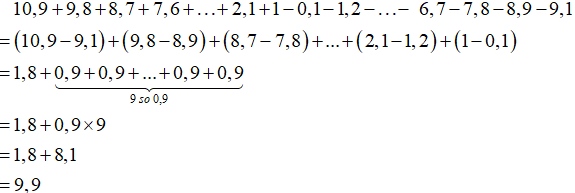
Ví dụ 2. Tính giá trị biểu thức sau: 

28,42 x 37,36 + 28,42 x 25,52 + 62,88 x 71,58

Bài giải

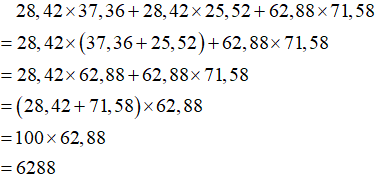
III. Tính nhanh dãy phân số có quy luật

Loại 1: Dãy phân số có quy luật mẫu số sau gấp mẫu số trước một số không đổi

Ví dụ 1:

Tính giá trị $A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$

Phân tích: Nhận xét thấy mẫu số phân số sau hơn mẫu số phân số trước 2 lần. Như vậy khi ta nhân thêm 2 vào thì phân số phía sau sẽ trở thành phân số phía trước.

Bài giải:

$A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$                      (1)

$2\times A=2\times \left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)$

$=\frac{2}{2}+\frac{2}{4}+\frac{2}{8}+\frac{2}{16}+\frac{2}{32}+\frac{2}{64}$

$=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}$                  (2)

Nhìn vào (1) và (2), chúng ta nhận thấy ở A và 2 x A có nhiều phân số giống nhau. Nếu ta trừ hai vế cho nhau thì được:

 $2\times A-A$= $\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)-$$\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)$

  $A=$ 1 – $\frac{1}{64}$= $\frac{63}{64}$

Ví dụ 2:

Tính $A=\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}+\frac{1}{729}$

Phân tích: Ở bài này, mẫu số sau gấp mẫu số trước 3 lần khi đó ta nhân biểu thức với 3 rồi trừ hai vế để triệt tiêu các phân số ở giữa.

Giải:

Ta có $A=\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}+\frac{1}{729}$

$3\times A=1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}$

Trừ hai vế ta có:

$3\times A-A=(1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243})-(\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}+\frac{1}{729})$

$2\times A=1-\frac{1}{729}=\frac{728}{729}$

$A=\frac{728}{729}:2=\frac{364}{729}$

Ví dụ 3:

Tính giá trị $A=\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+\frac{2}{24}+.....+\frac{2}{768}$

Ta thấy mẫu số của phân số sau gấp 2 lần mẫu số của phân số trước.

Ta có $2\times A=2\times (\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+\frac{2}{24}+....+\frac{2}{768})$

 $2\times A=\frac{4}{3}+\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+....+\frac{2}{384}$

$2\times A-A=\left(\frac{4}{3}+\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+....+\frac{2}{384}\right)-\left(\frac{2}{3}+\frac{2}{6}+\frac{2}{12}+\frac{2}{24}+....+\frac{2}{768}\right)$

$A=\frac{4}{3}-\frac{2}{768}=\frac{511}{384}$

Loại 2: Tính tổng của nhiều phân số có tử số là n (n > 0); mẫu số là tích của 2 thừa số có hiệu bằng n và thừa số thứ 2 của mẫu số phân số liền tr­ước là thừa số thứ nhất của mẫu số phân số liền sau

Ví dụ 1:

$A=\frac{1}{2\times 3}+\frac{1}{3\times 4}+\frac{1}{4\times 5}+\frac{1}{5\times 6}$

$A=\frac{3-2}{2\times 3}+\frac{4-3}{3\times 4}+\frac{5-4}{4\times 5}+\frac{6-5}{5\times 6}$

 = $\frac{3}{2\times 3}-\frac{2}{2\times 3}+\frac{4}{3\times 4}-\frac{3}{3\times 4}+\frac{5}{4\times 5}-\frac{4}{4\times 5}+\frac{6}{5\times 6}-\frac{5}{5\times 6}$

=  $\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}$

= $\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$

Ví dụ 2:

$B=\frac{3}{2\times 5}+\frac{3}{5\times 8}+\frac{3}{8\times 11}+\frac{3}{11\times 14}$

$B=\frac{5-2}{2\times 5}+\frac{8-5}{5\times 8}+\frac{11-8}{8\times 11}+\frac{14-11}{11\times 14}$

$=\frac{5}{2\times 5}-\frac{2}{2\times 5}+\frac{8}{5\times 8}-\frac{5}{5\times 8}+\frac{11}{8\times 11}-\frac{8}{8\times 11}+\frac{14}{11\times 14}-\frac{11}{11\times 14}$

$=\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}$

$=\frac{1}{2}-\frac{1}{14}=\frac{3}{7}$

IV. Bài tập về tính nhanh

Bài 1: Tính giá trị biểu thức số tự nhiên:

Bài 2: Tính giá trị biểu thức với phân số:

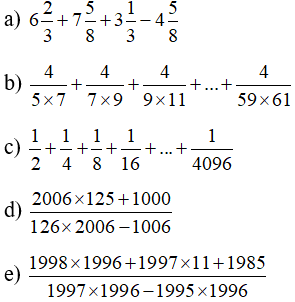
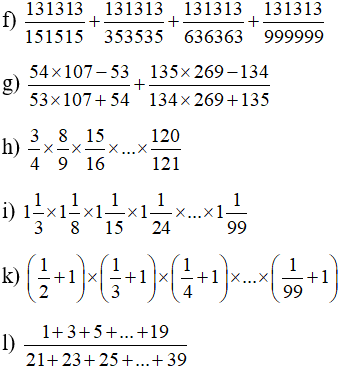
Bài 3: Tính giá trị biểu thức với số thập phân

Bài 4: Tính:

a. 70 – 49 : 7 + 3 × 6

b. 4375 × 15 + 489 × 72

c. (25915 + 3550 : 25) : 71

d. 14 × 10 × 32 : (300 + 20)

Bài 5: Tính:

a) (85,05 : 27 + 850,5) × 43 – 150,97

b) 0,51 : 0,17 + 0,57 : 1,9 + 4,8 : 0,16 + 0,72 : 0,9

Bài 6: Viết dãy số có kết quả bằng 100:

a) Với 5 chữ số 1.

b) Với 5 chữ số 5.

Bài 7: Cho dãy tính: 128 : 8 × 16 × 4 + 52 : 4. Hãy thêm dấu ngoặc đơn vào dãy tính đó sao cho:

a) Kết quả là nhỏ nhất có thể?

b) Kết quả là lớn nhất có thể?

Bài 8: Hãy điền thêm dấu ngoặc đơn vào biểu thức sau:

A = 100 – 4 × 20 – 15 + 25 : 5

a) Sao cho A đạt giá trị lớn nhất và giá trị lớn nhất là bao nhiêu?

b) Sao cho A đạt giá trị nhỏ nhất và giá trị nhỏ nhất đó là bao nhiêu?

Bài 9: Tìm giá trị số tự nhiên của a để biểu thức sau có giá trị nhỏ nhất , giá trị nhỏ nhất đó là bao nhiêu?

A = (a – 30) × (a – 29) × …× (a – 1)

Bài 10: Tìm giá trị của số tự nhiên a để biểu thức sau có giá trị lớn nhất, giá trị lớn nhất đó là bao nhiêu?

A = 2006 + 720 : (a – 6)

Bài 11: Tính giá trị của biểu thức m × 2 + n × 2 + p × 2, biết:

a) m = 2006, n = 2007, p = 2008

b) m + n + p = 2009

Bài 12: Tính giá trị của biểu thức M, với a = 119 và b = 0, biết:

M = b: (119 × a + 2005) + (119 : a – b × 2005)

Bài 13:Viết các tổng sau thành tích của hai thừa số:

a) 242 + 286 + 66

b) 6767 + 5555 + 7878

Bài 14: Tính nhanh:

a) 50 × 24,5 + 49 × 24,5 + 24,5

b) $\frac{7\times 5\times 12}{15\times 8\times 49}$

Bài 15: Cho biểu thức : A = (60 × 2 + 120 ) : 4; B = (30 × 4 + 120 ) : 8

Không tính giá trị nhưng giá trị của biểu thức nào lớn hơn, vì sao?

Bài 16: Tính giá trị biểu thức:

a) Bằng 2 cách: ( 27,8 + 16,4 ) × 5

b) Bằng cách nhanh nhất: (792,81 × 0,25 + 792,81 × 0,75) × (11 × 9 – 900 × 0,1- 9)

Bài 17: a) Tính giá trị biểu thức: 0,86 × 4,21 + ( 5,79 : 10 ) × 0,86 – 3,8

b) Tính nhanh: (156,2 + 3,8 – 17,5 + 252,5 – 197) × ( 0,2 – 2 : 10) × 2001

Bài 18: Với 4 chữ số 2 và các phép tính hãy lập các dãy tính có kết quả lần lượt là:

0; 1; 2; 3; 4; 5; 6; 8; 9; 10