Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bất phương trình mũ: Lý thuyết và các dạng bài tập. Tài liệu gồm vđầy đủ lý thuyết, phương pháp giải các dạng bài tập có lời giải chi tiết từ cơ bản đến nâng cao giúp học sinh ôn luyện kiến thức, nâng cao kĩ năng làm bài tập môn Toán 12.
Bất phương trình mũ: Lý thuyết và các dạng bài tập
1. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng ax > b ( hoặc ax < b; ) với a > 0 và a ≠ 1.
Ta xét bất phương trình ax > b
+ Nếu b ≤ 0 tập nghiệm của bất phương trình là vì ax > 0
+ Nếu b > 0 thì tập nghiệm của bất phương trình tương đương .
Với a > 1, tập nghiệm của bất phương trình là x > logab.
Với 0 < a < 1, tập nghiệm của bất phương trình là x < logab.
– Ví dụ 1.
a) 5x > 125x > log5125x > 3.
b)
Kết luận. Tập nghiệm của bất phương trình ax > b được cho trong bảng sau:
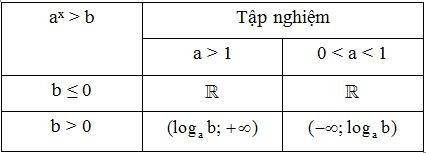
2. Dạng bài tập Bất phương trình mũ trong đề thi Đại học có lời giải
Phương pháp giải
• Bất phương trình dạng af(x) > ag(x) (a > 0; a ≠ 1)
+ Nếu a > 1 thì af(x) > ag(x) ⇔ f(x) > g(x).
+ Nếu 0 < a < 1 thì af(x) > ag(x) ⇔ f(x) < g(x).
• Bất phương trình dạng af(x) > b (a > 0; a ≠ 1)
+ Nếu b ≤ 0 thì ax > b ⇔ x ∈ R
+ Nếu a > 1 thì ax > b ⇔ x > logab
+ Nếu 0 < a < 1; b > 0 thì ax > b ⇔ x < logab
• Bất phương trình dạng ax > b (a > 0; a ≠ 1)
+ Nếu b ≤ 0 thì ax < b ⇔ x ∈ ø
+ Nếu a > 1; b > 0 thì ax < b ⇔ x < logab
+ Nếu 0 < a < 1; b > 0 thì ax < b ⇔ x > loga b
* Tương tự với bất phương trình dạng:
* Trong trường hợp cơ số a có chứa ẩn số thì: aM > aN ⇔ (a − 1)(M − N) > 0.
* Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
+ Đưa về cùng cơ số.
+ Đặt ẩn phụ.
+ Sử dụng tính đơn điệu của hàm số y= f( x) có tập xác định D:
Nếu hàm số đồng biến trên D thì f(u) < f(v) ⇔ u < v.
Nếu hàm số nghịch biến trên D thì f(u) < f (v) ⇔ u > v.
3. Phương pháp giải bất phương trình mũ
Bất phương trình mũ cơ bản có dạng ax > b (hoặc ax ≥ b, ax < b, ax ≤ b) với a > 0, a ≠ 1.
Ta xét bất phương trình có dạng ax > b.
• Nếu b ≤ 0, tập nghiệm của bất phương trình là R, vì ax > b, ∀x ∈ R..
• Nếu b > 0 thì bất phương trình tương đương với ax > alogab.
Với a > 1, nghiệm của bất phương trình là x > loga b.
Với 0 < a < 1, nghiệm của bất phương trình là x < loga b.
Ta minh họa bằng đồ thị sau:
• Với a > 1, ta có đồ thị sau.
• Với 0 < a < 1, ta có đồ thị sau.
Lưu ý:
1. Dạng 1:
2. Dạng 2:
3. Dạng 3: af(x) > b(*)
4. Dạng 4: af(x) < b(**)
Lưu ý: Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
Tương tự với bất phương trình dạng:
Trong trường hợp cơ số a có chứa ẩn số thì:
Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:
+ Đưa về cùng cơ số.
+ Đặt ẩn phụ.
+ Sử dụng tính đơn điệu:
Ví dụ 1: Giải bất phương trình sau
Hướng dẫn:
Ví dụ 2: Giải bất phương trình sau 9x-1-36.3x-3+3 ≤ 0
Hướng dẫn:
Biến đổi bất phương trình (1) ta được
(1) ⇔ (3x-1)2-4.3x-1+3 ≤ 0 (2)
Đặt t = 3x-1 (t > 0), bất phương trình (2) trở thành t2-4t+3 ≤ 0 (3)
(3) ⇔ 1 ≤ t ≤ 3
Suy ra: 1 ≤ 3x-1 ≤ 3 ⇔ 0 ≤ x-1 ≤ 1 ⇔ 1 ≤ x ≤ 2
Vậy tập nghiệm của bất phương trình là S = [1;2]
Ví dụ 3: Giải bất phương trình sau
Hướng dẫn:
Vì x2+1/2 > 0 nên ta có các trường hợp sau
Vậy nghiệm của bất phương trình là:
4. Bài tập tự luyện
Bài 1. Giải bất phương trình 3x2 − 9x + 6 > 3x − 3
A. 1 < x < 9 B. x > 1 C. x < 9 D. x > 9 hoặc x < 1
Đáp án: D
Bất phương trình 3x2 − 9x + 6 > 3x − 3
⇔ x2 − 9x + 6 > x − 3 (vì cơ số 3 > 1).
⇔ x2 − 10x + 9 > 0
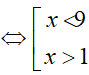
Bài 2.Có bao nhiêu giá trị nguyên của x thỏa mãn bất phương trình 
A. 6 B. 8 C. 7 D. 9
Đáp án: C
Điều kiện: x ∈ R (*)
Ta có: 
⇔ x2 − 6x + 4 < 4x − 5 (vì cơ số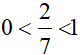 
)
⇔ x2 − 10x+ 9 < 0 hay 1 < x < 9
Mà x nguyên nên x ∈ { 2, 3, 4.., 7, 8}. Vậy có 7 giá trị nguyên của x thỏa mãn.
Bài 3. Bất phương trình 4x2 − 6x − 16 > 16x + 2 có số nghiệm nguyên dương ?
A.11 B. 0 C.1 D. Vô số.
Đáp án: D
Điều kiện: x ∈ R (*)
Ta có: 4x2 − 6x − 16 > 16x + 2 ⇔ 4x2 − 6x − 16 > 42(x + 2)
Do cơ số 2 > 1 nên bất phương trình trên tương đương với bất phương trình : x2 − 6x − 16 > 2(x + 2)
⇔ x2 − 8x − 20 > 0
x < −2 hoặc x > 10
Do đó, bất phương trình đã cho có vô số nghiệm nguyên dương.
Bài 4. Giải bất phương trình 32x+1 > 10
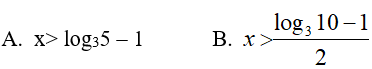
Đáp án: B
Điều kiện: x ∈ R (*)
Ta có: 32x+1 > 10 ⇔ 2x + 1 > log310
⇔ 2x > log310 − 1
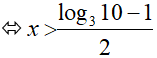
Bài 5. Giải bất phương trình 2x + 2x+1 > 3x + 3x+ 2
Đáp án: A
Điều kiện: x ∈ R (*)
Bất phương trình: 2x + 2x+1 > 3x + 3x+ 2
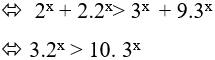
Bài 6. Tập nghiệm của bất phương trình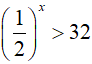 
là
A. x ∈ (−∞; 5). B. x ∈ (−∞; 5) C. x ∈ (−5; +∞) D. x ∈ (5; +∞)
Đáp án: A
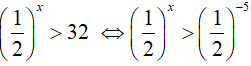
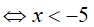
Bài 7. Tập nghiệm của bất phương trình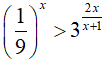 
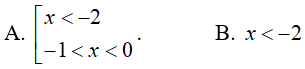
là
Đáp án: A
Điều kiện: x ≠ −1
Ta có:
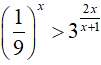
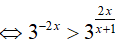
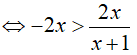
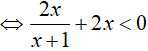
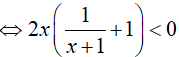
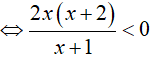
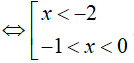
Kết hợp với điều kiện
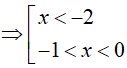
Bài 8. Tập nghiệm của bất phương trình 16x − 4x − 6 ≤ 0 là
A. x ≤ log43. B. x > log43. C. x ≥ 1. D. x ≥ 3
Đáp án: A
Điều kiện: x ≠ −1
Ta có: 16x − 4x − 6 ≤ 0 ⇔ 42x − 4x − 6 ≤ 0
Đặt t= 4x ( t > 0), khi đó bất phương trình đã cho tương đương với:
t2 − t − 6 ≤ 0 ⇔ −2 ≤ t ≤ 3
Mà t > 0 nên 0 < t ≤ 3 ⇔ x ≤ log43
Bài 9. Tập nghiệm của bất phương trình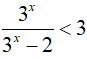 
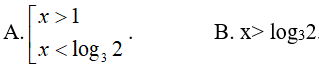
là:
Đáp án: A
Ta có:
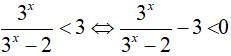
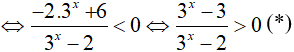
Đặt t= 3x > 0, khi đó ( *) trở thành:
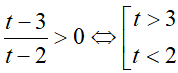
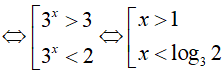
Bài 10. Tập nghiệm của bất phương trình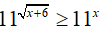 
là:
Đáp án: A
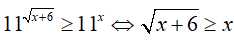
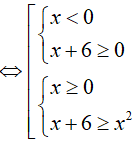
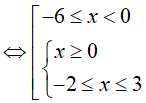
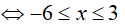
Bài 11. Tập nghiệm của bất phương trình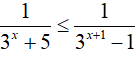 
là:
Đáp án: A
Ta có:
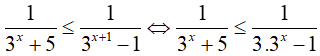
Đặt t=3x (t > 0 ) , khi đó bất phương trình đã cho tương đương với
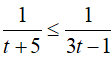
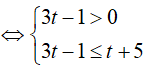
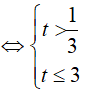
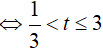
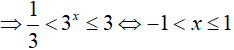
Bài 12. Tập nghiệm của bất phương trình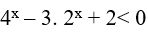 
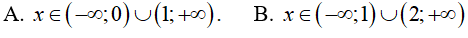
là:
Đáp án: C
Ta có:
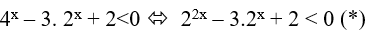
Đặt t=2x (t > 0 ) , khi đó bất phương trình đã cho tương đương với
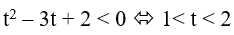
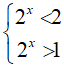
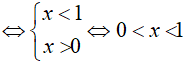
Bài 13. Tập nghiệm của bất phương trình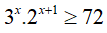 
là:
Đáp án: A
Ta có:
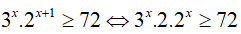
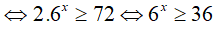
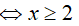
Bài 14. Tập nghiệm của bất phương trình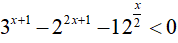 
là:
Đáp án: A
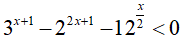
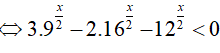
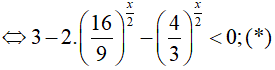
Đặt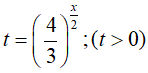 
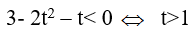
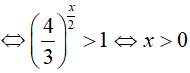
. Khi đó, phương trình ( *) trở thành:
Bài 15. Tập nghiệm của bất phương trình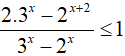 
là:
Đáp án: C
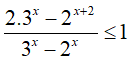
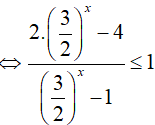
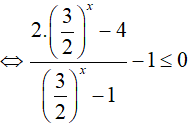
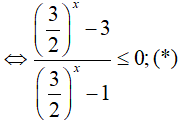
Đặt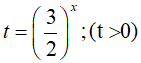 
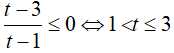
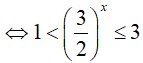
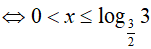
. Khi đó, phương trình ( *) trở thành:
Bài 16. Tập nghiệm của bất phương trình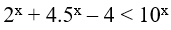 
là:
Đáp án: C
Ta có:
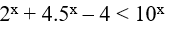
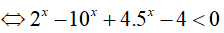
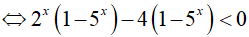
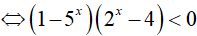
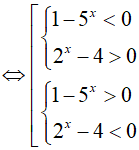
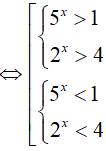
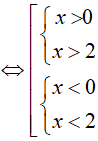
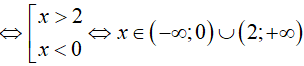
Bài 17. Tập nghiệm của bất phương trình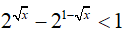 
là:
Đáp án: C
Điều kiện: x ≥ 0
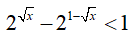
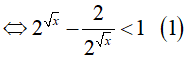
Đặt t = 2√x. Do x ≥ 0 => t ≥ 1
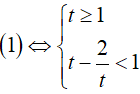
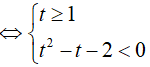
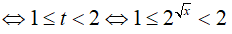
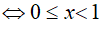
Bài 18. Cho bất phương trình: 
. Tìm tập nghiệm của bất phương trình.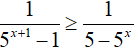
A. S = (−1; 0] ∪ (1; +∞) B. S = (−1; 0] ∩ (1; +∞)
C. S = (−∞; 0] D. S = (−∞; 0)
Đáp án: A
Điều kiện: x ≠ ±1
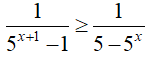
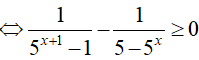
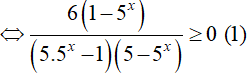
Đặt t = 5x. BPT(1)
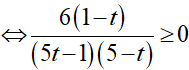
Đặt
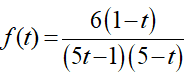
Lập bảng xét dấu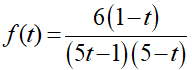 
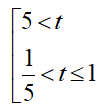
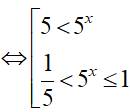
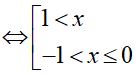
, ta được nghiệm của BPT (*) là:
Vậy tập nghiệm của BPT là S = (−1; 0] ∪ (1; +∞)
Bài 19. Với giá trị nào của tham số m thì bất phương trình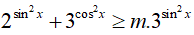 
có nghiệm?
A. m ≤ 2. B. m ≥ 4. C. m ≤ 4. D. m ≥ 1
Đáp án: C
Chia hai vế của bất phương trình cho 3sin2x > 0 , ta được
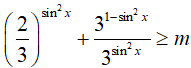
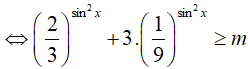
Xét hàm số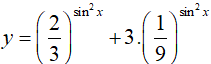 
là hàm số nghịch biến.
Ta có: 0 ≤ sin2x ≤ 1 nên 1 ≤ y ≤ 4
Vậy bất phương trình có nghiệm khi m ≤ 4.
Bài 20. Cho bất phương trình: 9x + ( m − 1).3x + m > 0 (1). Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀x > 1 .
Đáp án: A
Đặt t = 3x ( t > 0) .Vì x > 1 nên t > 3.
Bất phương trình đã cho thành: t2 + (m − 1)t + m > 0 nghiệm đúng ∀t ≥ 3
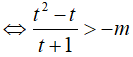
nghiệm đúng ∀t > 3 .
Xét hàm số
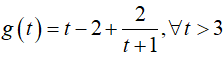
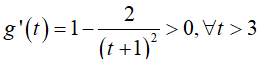
Hàm số đồng biến trên [3; +∞) và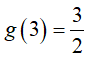 
.
Yêu cầu bài toán tương đương
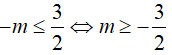
Bài 21. Cho hàm số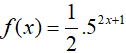 
và g(x)=5x + 4x. ln5. Giá trị nguyên lớn nhất của x sao cho f’(x) < g’(x) là.
A. −2 B. −1 C. 1 D. 2
Đáp án: B
Ta có:
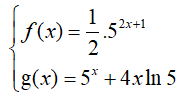
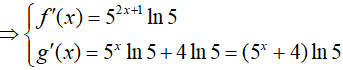
Khi đó: f’(x) < g’(x) ⇔ 52x+1.ln 5 < (5x + 4).ln 5
⇔ 52x+1 < 5x +4 ⇔ 5.52x − 5x − 4 < 0
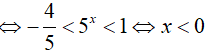
Do đó, giá trị nguyên lớn nhất thỏa mãn đầu bài là x = −1.
Bài 22. Gọi x0 là nghiệm nhỏ nhất của bất phương trình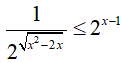 
. Tìm x0 ?
Đáp án: C
Bất phương trình tương đương:
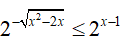
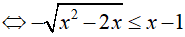
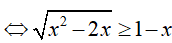
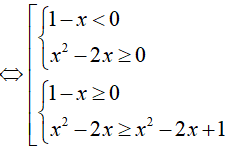
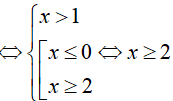
Do đó,nghiệm nhỏ nhất của bất phương trình đã cho là x0 = 2.
Bài 23. Số nghiệm nguyên của bất phương trình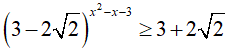 
là.
A. 2 B. 4 C. 3 D. vô số.
Đáp án: B
Ta thấy: (3 − 2√2).(3 + 2√2) = 9 − 8 = 1 nên:
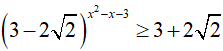
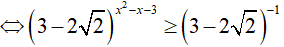
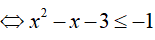
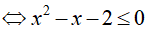
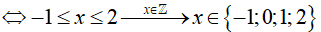
Vậy bất phương trình đã cho có 4 nghiệm nguyên .
Bài 24. Cho bất phương trình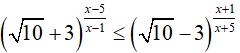 
. Gọi x1, x2 lần lượt là nghiệm nguyên lớn nhất và nhỏ nhất của bất phương trình. Khi đó x1 + x2 bằng bao nhiêu?
A. < 2 B. 1 C. 0 D. < 1
Đáp án: D
Ta có:
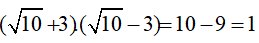
nên:
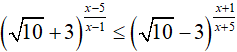
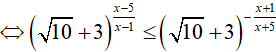
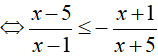
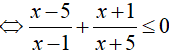
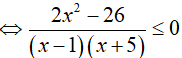
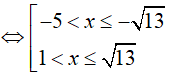
Do đó, nghiệm nguyên lớn nhất và nghiệm nguyên nhỏ nhất của bất phương trình đã cho là 3 và −4. Suy ra, x1 + x2 = −1
Bài 25. Tìm số nguyên lớn nhất của m để bất phương trình: 9x − 2(m + 1).3x − 3 − 2m > 0 nghiệm đúng với mọi x ∈ R
A. m = −1 B.m = −2 C. m = 0 D. m = −3
Đáp án: A
Đặt t= 3x ; (t > 0).
Khi đó yêu cầu bài toán trở thành: Tìm số nguyên lớn nhất của m để bất phương trình:
t2 − 2(m + 1)t − 3 − 2m > 0 đúng với mọi m (*)
Cách 1:
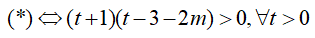
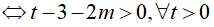
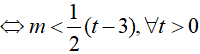
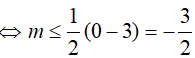
Suy ra, số nguyên lớn nhất của m thỏa mãn là m = −1.
Cách 2:
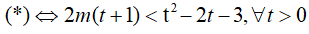
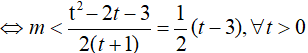
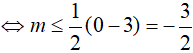
Bài 26. Tìm tất cả các giá trị của tham số m để bất phương trình 4x − 2x − m ≥ 0 có nghiệm đúng với mọi x
Đáp án: C
Đặt t =2x ( t > 0). Khi đó bất phương trình có dạng: t2 < t < m ≥ 0
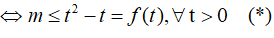
Ta có
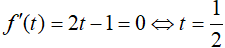
BBT:
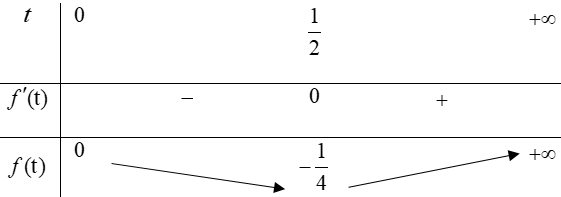
Khi đó:
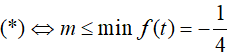
Vậy
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
