Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu bài tập Số phức là gì? Lý thuyết và các dạng bài tập thường gặp, tài liệu bao gồm 7 dạng bài tập Số phức đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi tốt nghiệp THPT môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Số phức là gì? Lý thuyết và các dạng bài tập thường gặp
1. Khái niệm số phức
· Tập hợp số phức: C
· Số phức (dạng đại số) :
(a, b, a là phần thực, b là phần ảo, i là đơn vị ảo, i2 = –1)
· z là số thực phần ảo của z bằng 0 (b = 0)
z là thuần ảo phần thực của z bằng 0 (a = 0)
Số 0 vừa là số thực vừa là số ảo.
Hai số phức bằng nhau:
Chú ý:
2. Biểu diễn hình học:
Số phức z = a + bi (a, b được biểu diễn bởi điểm M(a; b) hay bởi trong mp(Oxy) (mp phức)
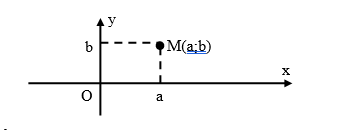
3. Cộng và trừ số phức:
· ·
· Số đối của z = a + bi là –z = –a – bi
· biểu diễn z, biểu diễn z' thì biểu diễn z + z’ và biểu diễn z – z’.
4. Nhân hai số phức:
·
·
5. Số phức liên hợp của số phức z = a + bi là
z là số thực ; z là số ảo
6. Môđun của số phức: z = a + bi
7. Bài tập tự luyện
Bài 1: Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
Lời giải:
Ta có z1− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
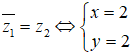
Vậy x= 2, y = 2.
Bài 2: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
Lời giải:
Ta có |1 + i| = . Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| ⇔ OM =
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= .
Bài 3: Phần thực của số phức z = -i là
Lời giải:
Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0
Bài 4: Phần ảo của số phức z = -1 là
Lời giải:
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Bài 5: Số phức liên hợp của số phức z = 1 + i là
Lời giải:
Số phức liên hợp của số phức z = 1 + i là z− = 1 - i
Bài 6: Cho z = 2i -1. Phần thực và phần ảo của z− là
Lời giải:
Ta có z = 2i - 1 = -1 + 2i ⇔ z− = -1 - 2i. Vậy phần thực của z− là -1 và phần ảo của z− là -2.
Bài 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Lời giải:
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Bài 8: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là?
Lời giải:
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Bài 9: Môđun của số phức z thỏa mãn z− = 8 - 6i là
Lời giải:
Ta có
Bài 10: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Lời giải:
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Vậy x = -3, y = 1.
Bài 11: Môđun của số phức z = -3 + 4i là
A. 5
B. -3
C. 4
D. 7
Lời giải:
Ta có: z = -3 + 4i
Bài 12: Môđun của số phức z = 2 - i là
A.
B. 2 +
C. 2 -
D. 7
Lời giải:
Ta có: z = 2 - i
Bài 13: Số phức z = 1 - 2i có điểm biểu diễn là
A. M (1; 2)
B. M (1; -2)
C. M (-1; 2)
D. M (-1; -2)
Lời giải:
Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).
Bài 14: Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua
A. Trục tung
B. Trục hoành
C. Gốc tọa độ
D. Điểm I (1; -1)
Lời giải:
Hai điểm biểu diễn của z = 1 + i và z− = 1 - i là M(1; 1) và N(1; -1) đối xứng với nhau qua trục Ox.
Bài 15: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là
A. Hai đường thẳng
B. Đường tròn bán kính bằng 2
C. Đường tròn bán kính bằng 4
D. Hình tròn bán kính bằng 2.
Lời giải:
Gọi M là diểm biểu diễn của z. Ta có: |z| = 2 ⇔ OM = 2
Vậy quỹ tích của M là đường tròn tâm là gốc tọa độ O và bán kính R = 2.
Bài 16: Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là
A.
B.
C.
D. 10
Lời giải:
Ta có: A(-1;2), B(2,3). Do đó:
Bài 17: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
Lời giải:
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Chọn đáp án C.
Bài 18: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3
B. -1 và -3
C. 1 và -3
D. -1 và -3i.
Lời giải:
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Bài 19: Môđun của số phức z thỏa mãn z− = 8 - 6i là
A. 2
B. 10
C. 14
D. 2
Lời giải:
Ta có
Chọn đáp án B.
Bài 20: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1
B. x = 3, y = -1
C. x = -3, y = -1
D. x = -3, y = 1
Lời giải:
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
Vậy x = -3, y = 1.
Chọn đáp án D.
Bài tập số phức cơ bản trong đề thi Đại học có lời giải (6 dạng)
Dạng 1: Cộng, trừ số phức
1. Phương pháp giải
Cho hai số phức z1 = a + bi và z2 = c + di thì:
• Phép cộng số phức: z1 + z2 = (a + c) + (b + d)i
• Phép trừ số phức: z1 – z2 = ( a- c) + ( b – d) i
2. Ví dụ minh họa
Ví dụ 1: Cho hai số phức z1 = 1 + 10i và z2 = 9 – 2i. Số phức z = z1 + z2 có z1 có phần thực là:
A. 8 B. 10 C. 12 D. 14
Lời giải:
Ta có:
z = z1 + z2 = (1 + 10i) + ( 9 – 2i) = 10 + 8i.
Do đó, phần thực của số phức z là 10.
Đáp án: B
Ví dụ 2:Hãy tính số phức z. Biết rằng: z = 10i – ( 2 + 2i).i
A. z = 2 + 8i B. z = 8 - 2i
C. z = 8 + 2i D. z = 2 - 8i
Lời giải:
Ta có z = 10i - (2 + 2i).i = 10i – 2i + 2 = 2 + 8i
Đáp án: A
Ví dụ 3: Cho hai số phức z = -2 + 3yi; z’ = ( x + 1)- 4i với x,y ∈ R . Tìm x; y để z + i= z’ + 2
A. x = -5; y =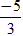 
B. x = 5; y = 2
C. x = 2; y =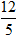 
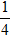
D. x = 
; y = -2
Lời giải:
Để z + i = z’ + 2 ⇔ - 2 + 3yi + i = ( x + 1) – 4i + 2
⇔ - 2 + (3y + 1).i = ( x + 3)- 4i
Do đó ta có hệ phương trình :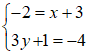
⇔ 
Đáp án: A
Ví dụ 4: Cho z1 = a + 8i ,z2 = 6 – 3i và z3 = 10 + bi ( a,b ∈ R ). Tìm a, b để z1 + z2 = z3
A. a = 2; b = 5 B. a = 1; b = -5
C. a = 4; b = 5 D. a = 3; b = 1
Lời giải:
Ta có: z1 + z2 = z3 nên (a + 8i) + ( 6 – 3i) =10 + bi
⇔ ( a + 6) + 5i = 10 + bi
⇔ 
⇔ 
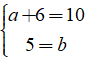
Vậy a = 4; b= 5.
Đáp án: C
Ví dụ 5: Số nào trong các số phức sau là số thuần ảo?
A. (√2 + i) - (1 + √2i) B. ( 8 + 2i) + (- 8 + 2i)
C. ( - 3 + i) – ( 3 - i) D. (10 + 3i) – ( -10 – 3i)
Lời giải:
Ta xét các phương án:
* (√2 + i) - (1 + √2i)= (√2 - 1) - (1 - √2) không là số thuần ảo.
* (8 + 2i) + (- 8 + 2i) = 4i là số thuần ảo.
* (-3 + i) – (3- i) = - 3 + i – 3 + i= - 6 + 2i không là số thuần ảo.
* (10 + 3i) – ( -10 – 3i) = 10 + 3i + 10 + 3i = 20 + 6i không là số thuần ảo.
Đáp án: B
Dạng 2: Nhân, chia hai số phức
1. Phương pháp giải
Phép nhân số phức: z1.z2 = ( ac – bd) + ( ad + bc). i
Phép chia số phức:
• Số phức nghịch đảo của z = a + bi ≠ 0
là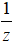 
= 
= 
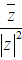
• Thực hiện phép chia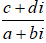 
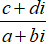
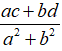
là nhân cả tử và mẫu với số phức liên hợp của a + bi
= 
= 
+ 
2. Ví dụ minh họa
Ví dụ 1: Tính giá trị của P= i105 + i23 + i20 – i34
A. 1 B. -2 C. 2 D. 5
Lời giải:
Ta có : i2 = -1 ⇒ i4 = 1.
Do đó, P = i105 + i23 + i20 – i34
= i104 + 1 + i20 + 3 + i4.5 – i4.8 + 2
= i. i4.26 + i2.i.i4.5 + 1- i2. i4.8
= i. 1 + (-1).i.1 + 1 - (-1).1 = 2
Đáp án: C
Ví dụ 2: Tìm số phức z = [(1 + 5i) - (1 + 3i)]2007.
A. z= - 82007.i B. z= -82007.i
C. z= -22007 D. z= -22007.i
Lời giải:
z = [(1 + 5i) - (1 + 3i)]2007 ⇔ z = [2i]2007
⇔ z = 22007i2007
⇔ z = 2 2007 i4.501.i2.i=2 2007 (-i) ( Vì i2 = -1 nên i4 =1)
Đáp án: D
Ví dụ 3: Gía trị của biểu thức A =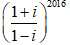 
+ 
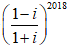
bằng
A. 1 + i B. 2 C. 0 D. -2
Lời giải:
Ta có:
= 
= 
= 
= i
= 
= 
= 
= - i ;
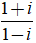
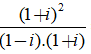
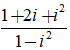
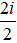
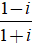
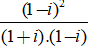
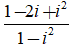
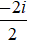
Suy ra:
A =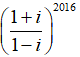 
+ 
= i2016 + (-i)2018
= (i2)1008 + (i2)1009 = (-1)1008 + (-1)1009
= 1-1 = 0
Đáp án: C
Ví dụ 4: Cho P= 1 + i + i2 + i3 + ... + i2017. Tính P?
A. P= i + 1 B. P= 1 C. P= i D. P= 2i
Lời giải:
Ta có;
P= 1 + i + i2 + i3 + ... + i2017
iP= i + i2 + i3 + ... + i2018
⇒ P - iP = 1 - i2018
⇒ P =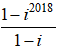 
= 
= 
= 
= 
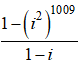
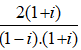
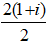
= 1 + i
Đáp án: A
Ví dụ 5: Cho A = 1 + i2 + i4 + .. + i4k-2 + i4k với k là số nguyên dương. Tính A?
A. A = 2ki B. A = 2k C. A = 0 D. A = 1
Lời giải:
Do A là tổng của một cấp số nhân (gồm 2k + 1 số hạng) với số hạng đầu u1 = 1, công bội q= i2.
Suy ra
A = 1 + i2 + i4 + .. + i4k-2 + i4k
= 
= 
= 
= 1
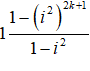
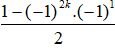
Đáp án: D
Dạng 3: Tìm số phức liên hợp
1. Phương pháp giải
Cho số phức z= a + bi,( a,b ∈ R). Khi đó, số phức liên hợp với số phức z là: z− = a - bi
2. Ví dụ minh họa
Ví dụ 1: Tìm số phức liên hợp của số phức
z = ( 3- 2i). (2 + 3i)
A. z− = -5i B. z− = 12 -5i
C. z− = 12 + 5i D. z− = 3 + 2i
Lời giải:
Ta có: z = (3 - 2i).(2 + 3i) = 6 + 9i – 4i + 6
⇔ z = 12 + 5i Do đó, số phức liên hợp với số phức z là z− = 12 -5i
Đáp án: B
Ví dụ 2: Cho số phức z = 5 – 3i. Tính 1 + z− + (z− )2 ta được kết quả:
A. – 22 + 33i. B. 22 + 33i.
C. 22 - 33i. D. -22 - 33i.
Lời giải:
Ta có z = 5 - 3i ⇒ z− = 5 + 3i
Suy ra : 1 + z− + (z− )2 = 1 + (5 + 3i) + (5 + 3i)2 = (6 + 3i) + (25 + 30i - 9) = 22 + 33i
Đáp án: B
Ví dụ 3: Cho số phức z = 4 - 3i. Tìm số phức liên hợp của số phức ω = 2z− + z2.
A. ω− = 15 - 18i B. ω− = 16 + 18i
C. ω− = 15 + 16i D. ω− = 15 + 18i
Lời giải:
Ta có z = 4 - 3i nên số phức liên hợp với số phức z là : z− = 4 + 3i
Theo đầu bài :
ω = 2z− + z2 = 2. (4 + 3i) + ( 4-3i)2
⇔ ω = 8 + 6i + ( 16 – 24i + 9i2) = 15 – 18i
Vậy ω = 15 – 18i
Vậy số phức liên hợp của ω là
ω− = 15 + 18i
Đáp án: D
Ví dụ 4: Cho số phức z thỏa mãn (1 + 3i) z - (2 + 5i) = (2 + i) z. Tìm số phức liên hợp của số phức z.
A. z− =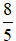 
+ 
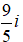
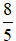
B. z− = - +
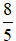
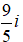
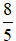
C. z− = - D. z− = - -
Lời giải:
Theo giả thiết ta có:
(1 + 3i)z-(2 + 5i) = (2 + i)z
⇔(1 + 3i-2-i)z = 2 + 5i⇔(-1 + 2i)z = 2 + 5i
⇔z =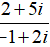 
= +
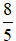
Đáp án: A
Ví dụ 5: Tìm số phức z, biết z + 2iz− + 4 = i
A. z = 2- 3i B. z = - 3 + 2i
C. z = - 2 + 3i D. z = 3 - 2i
Lời giải:
Gọi số phức z cần tìm là z = a + bi ( a,b ∈ R)
Số phức liên hợp với số phức z là : z− = a - bi
Theo giả thiết: z + 2iz− + 4 = i
⇒ a + bi + 2i(a - bi) + 4 = i
⇔ a + bi + 2ai + 2b + 4-i = 0
⇔(a + 2b + 4) + (b + 2a-1)i = 0
⇔ 
⇔ 
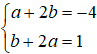
Suy ra z = 2- 3i
Đáp án: A
Dạng 4: Môđun của số phức
1. Phương pháp giải
* Cho số phức z = a + bi, ( a,b ∈ R). Khi đó mô đun của số phức z kí hiệu là : | z| và :
| z| = 
* Nhận xét : |z| ≥ 0 và |z| = 0 ⇔ z = 0 .
2. Ví dụ minh họa
Ví dụ 1: Tính môđun của số phức z = 6 – 8i
A. 10 B. 2 C. -2 D. 80
Lời giải:
Môđun của số phức z = 6 – 8i là: | z| =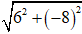 
= 10
Đáp án: A
Ví dụ 2: Tìm số phức z, biết | z| = √5 , phần thực bằng 2 lần phần ảo và phần thực dương
A. z = 2 + i B. z = 1 + 2i
C. z =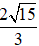 
+ 
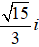
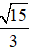
D. z = 
+ 
Lời giải:
Cho số phức z = a + bi, ( a,b ∈ R) và a > 0
Do phần thực bằng 2 lần phần ảo nên: a = 2b (1).
mà | z| = √5 ⇔ 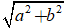= √5 ⇔ a2 + b2 = 5 (2)
Từ (1) và (2) ta có hệ phương trình :
⇔ 
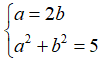
Vậy số phức cần tìm là z = 2 + i.
Đáp án: A
Ví dụ 3: Cho số phức z có phần thực là số nguyên và z thỏa mãn: | z| - 2z− = -7 + 3i + z . Tính môđun của số phức: ω = 1 - z + z2
A. |ω| = √37 B. |ω| = √457
C. |ω| = √425 D. |ω| = 457
Lời giải:
Gọi số phức cần tìm là z = a + bi, ( a,b ∈ R)
Số phức liên hợp của số phức z là : z− = a - bi và | z| =
Theo giả thiết ta có: | z| - 2z− = -7 + 3i + z
⇔ - 2(a - bi) = -7 + 3i + a + bi
⇔ 
⇔ 
⇔ 
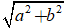
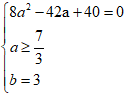
vậy z = 4 + 3i ⇒ ω = 1-(4 + 3i) + (4 + 3i)2 = 4 + 21i⇒ |ω| =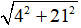 
= √457
Đáp án: B
Ví dụ 4: Cho hai số phức z1 và z2 thỏa Cho hai số phức z1 và z2 thỏa |z1 | = |z2 | = 1; |z1 + z2 |=√3. Tính |z1 - z2 |
A. √3-1 B. 0 C. 1 D. -1
Lời giải:
Ta có :
3 =|z1 + z2 |2 = (z1 + z2 )( z− 1 + z− 2 )
⇒z1 z− 2 + z2 z− 1 + z1 z− 1 + z2 z− 2 = 3
⇒z1 z− 2 + z2 z− 1 = 1
Vì |z1| = |z2| = 1 nên z1. z1− = 1 ; z2. z2− = 1
Khi đó:
|z1 - z2|2 = (z1 - z2)(z1− - z2− ) = |z1|2 + |z2|2 - (z1 z2− + z2 z1− ) = 1
Đáp án: C
Ví dụ 5: Cho số phức z thỏa mãn | z + 3| = 5 và | z- 2i|= |z – 2 - 2i|. Tính |z|.
A. |z| = 5 B. |z| = √5
C. |z| = 2 D. |z| = √10
Lời giải:
Gọi số phức z cần tìm là z = a + bi ( a,b ∈ R)
Ta có: |z + 3| = 5⇔|a + bi + 3| = 5 ⇔(a + 3)2 + b2 = 25 (*)
|z-2i| = |z-2-2i| ⇔|a + bi-2i| = |a + bi-2-2i|
⇔a2 + (b-2)2 = (a - 2)2 + (b - 2)2
⇔a2 = (a-2)2
⇔ 
Thế a = 1 vào (*) ta được 16 + b2 = 25 ⇒ b2 = 9
Do đó, môdun của z là: |z| =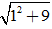 
= √10
Đáp án: D
Dạng 5: Tìm số phức thỏa mãn điều kiện T
1. Phương pháp giải
Để tìm được số phức thỏa mãn điều kiện T, ta cần linh hoạt các phép toán của số phức, tính môdun số phức, số phức liên hợp...
2. Ví dụ minh họa
Ví dụ 1: Cho số phức z = 2m + ( m + 2)i, (m∈ R) . Tìm z biết rằng z2 là một số phức có phần thực bằng - 5.
A. Không có số phức cần tìm
B. z = 2 + 3i , z =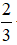 
+ 
C. z = 4 + 2√3 + (4 + √3)i; z = 4 - 2√3 + (4 - √3)i
D. z = 2i, z = -18 – 7i
Lời giải:
Ta có :
z2 = 4m2 + 2m(m + 2)i + [(m + 2)i]2 = 3m2 + 2m(m + 2)i-4m-4
Do z2 là số phức có phần thực bằng -5 nên ta có:
⇒ 3m2 - 4m - 4 = -5 ⇔ 3m2 - 4m + 1 = 0 ⇔ m = 1 ; m = 1/3
Vậy có hai số phức thỏa mãn là z1 = 2 + 3i và z2 = +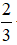
Đáp án: B
Ví dụ 2: Cho số phức z = m + (m-1)i; (m∈ R) và số phức z' = 2n + (2-3n)i (n∈R) .Tìm m và n biết rằng z - z’= 1 + 7i
A. m =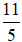 
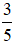
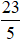
; n = 
B. m = 
; n = 
C. m = -9, n = -5 D. m = -13, n = - 7
Lời giải:
Ta có:
z - z’ = [ m + ( m - 1).i] – [2n + (2- 3n).i] = (m- 2n) + ( m + 3n – 3). I
Theo giả thiết z- z’ = 1 + 7i nên ta có: (m - 2n) + (m + 3n – 3).i = 1 + 7i .
Từ đó ta có hệ phương trình sau:
⇔ 
⇔ 
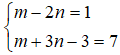
Đáp án: B
Ví dụ 3: Tìm số phức z = x + yi, ( x, y ∈ R) thỏa mãn z + 3x = 2z− - 3i . Tìm |z|
A. |z| = 1 B. |z| = 2
C. |z| = √2 D. |z| = √3
Lời giải:
Vì z + 3x = 2z− - 3i
⇔ x + yi + 3x = 2(x - yi) - 3i
⇔ 4x + yi = 2x - (2y + 3)i
⇔ 
⇔ 
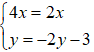
Do đó, số phức thỏa mãn đầu bài là z = - i và |z| = 1
Đáp án: A
Ví dụ 4: Có bao nhiêu số phức z có phần ảo gấp ba lần phần thực, đồng thời |z− | = 
A. 0 B. 1 C. 2 D. 3
Lời giải:
Gọi số phức cần tìm là z = a + bi, ( a,b ∈ R)
Do số phức z có phần ảo gấp ba lần phần thực nên b = 3a
⇒ Số phức cần tìm có dạng: z = a + 3ai
Số phức liên hợp của số phức z là: z− = a - 3ai
Theo giả thiết ta có: |z−| =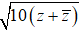 
⇔ 
= 
⇔ 
= 
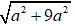
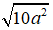
⇔ 10a2 = 20a ⇔ 
Với a = 0 thì z = 0.
Với a = 2 thì z = 2 + 6i
Vậy có hai số phức thỏa mãn là z = 0 hoặc z = 2 + 6i
Đáp án: C
Ví dụ 5: Trong mặt phẳng Oxy cho điểm A là điểm biểu diễn của số phức z= 1 + 2i, B là điểm thuộc đường thẳng y=2 sao cho tam giác OAB cân tại O. Tìm số z biểu diễn B.
A. z = 1 + 2i. B. z = -1 + 2i.
C. z = 3 + 2i, z = -3 + 2i. D. z = - 1 + 2i, z = 1 + 2i.
Lời giải:
Ta có, điểm A biểu diễn số phức z = 1 + 2i nên tọa độ A( 1; 2) .
Do điểm B nằm trên đường thẳng y = 2 nên tọa độ B(x, 2); ( x ≠ 1 )
Để tam giác OAB cân tại O khi và chỉ khi OA = OB.
⇔ 
= 
⇔ x2 + 4 = 5
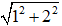
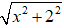
⇔ x2 = 1 ⇔ 
Suy ra, tọa độ B (-1; 2). Do đó,số phức biểu diễn B là z = -1 + 2i
Đáp án: B
Dạng 6: Giải phương trình bậc nhất trên tập số phức
1. Phương pháp giải
Cho phương trình az + b= 0 (a ≠ 0 ) a, b là hai số phức ⇔ az = -b ⇔ z = 
Sau đó, thực hiện phép chia số phức để tìm ra z.
2. Ví dụ minh họa
Ví dụ 1:Cho số phức z thỏa mãn: (2 + i)z + 2 – i= 0. Tìm phần thực của số phức.
A. - 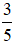B. -3 C. 5 D. 
Lời giải:
Ta có: (2 + i ).z + 2- i = 0 ⇔ ( 2 + i)z = - 2 + i
⇔ z =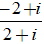 
= 
⇔ z =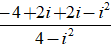 
= 
Do đó, phần thực của số phức cần tìm là -
Đáp án: A
Ví dụ 2: Giải phương trình iz + 3- 2i = 1 + i
A. z = 2 + 3i B. z = 1- 3i
C. z = 3 + 2i D. z = 2 + 2i
Lời giải:
Ta có: iz + 3 – 2i = 1 + i
⇔ iz = 1 + i- 3 + 2i
⇔ iz = -2 + 3i
⇔ z =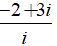 
= 
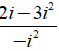
= 3 + 2i
Đáp án: C
Ví dụ 3: Giải phương trình: (2 + 4i)z + ( 4 - 2i)z + 2- 2i = 0
A. z =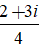 
B. z = 
C. z =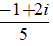 
D. z = 
Lời giải:
Ta có: ( 2 + 4i).z + (4 –2 i). z + 2- 2i = 0
⇔( 2 + 4i + 4 – 2i)z = - 2 + 2i ⇔ (6 + 2i). z = - 2 + 2i
⇔ z =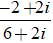 
= 
⇔z = 
⇔ z =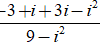 
= 
= 
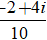
Đáp án: C
Ví dụ 4: Giải phương trình (1 + 2i)z +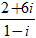 
= 0
A. z =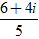 
B. z = 
C. z =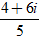 
D. z = 
Lời giải:
Ta có: (1 + 2i)z + 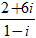= 0 ⇔ (1 + 2i)z =
⇔ (1 + 2i)z = 
⇔ (1 + 2i)z = 
⇔ (1 + 2i)z = 
⇔ (1 + 2i)z = -2 + 4i
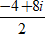
⇔ z =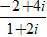 
= 
⇔ z = 
⇔ z =
Đáp án: D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
