Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Đường cao là gì? Tính chất đường cao và các dạng bài tập về đường cao, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Đường cao, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.

Đường cao là gì? Tính chất đường cao và các dạng bài tập về đường cao

A. Lý thuyết Đường cao

1. Đường cao của tam giác là gì?

• Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

• Mỗi tam giác có ba đường cao.

2. Tính chất đường cao trong tam giác

Định lí: Ba đường cao của một tam giác cùng đi qua một điểm.

Ví dụ: Trong hình vẽ dưới đây ba đường cao AD, BE, CF của tam giác ABC cùng đi qua điểm H. Điểm H được gọi là trực tâm của tam giác ABC.

Chú ý:

(1) Tam giác nhọn có trực tâm nằm bên trong tam giác (như hình vẽ dưới đây).

Tam giác ABC nhọn có trực tâm H nằm trong tam giác.

(2) Tam giác vuông có trực tâm trùng với đỉnh góc vuông (như hình vẽ dưới đây).

Tam giác EGF có trực tâm H trùng với đỉnh góc vuông E.

(3) Tam giác tù có trực tâm nằm ngoài tam giác (như hình vẽ dưới đây)

Tam giác tù BCD có tực tâm H nằm ngoài tam giác.

3. Công thức tính đường cao

a. Công thức tính đường cao trong tam giác thường

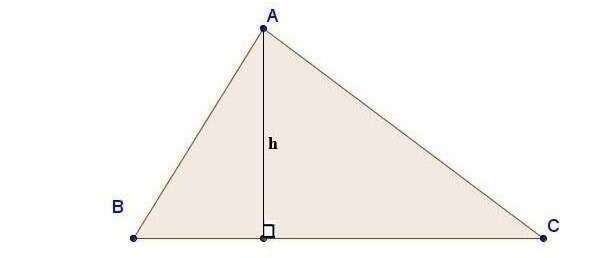
Cách tính đường cao trong tam giác sử dụng công thức Heron:

Với a, b, c là độ dài các cạnh; ha là đường cao được kẻ từ đỉnh A xuống cạnh BC; p là nửa chu vi:

b. Công thức tính đường cao trong tam giác đều

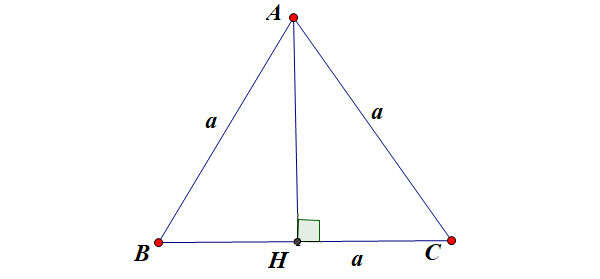
Giả sử tam giác đều ABC có độ dài cạnh bằng a như hình vẽ:

Trong đó:

• h là đường cao của tam giác đều
• a là độ dài cạnh của tam giác đều

c. Công thức tính đường cao trong tam giác vuông

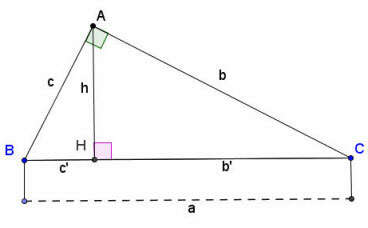
Giả sử có tam giác vuông ABC vuông tại A như hình vẽ trên:

Công thức tính cạnh và đường cao trong tam giác vuông:

1. a² = b² + c²

2. b² = a.b′ và c² = a.c′

3. a.h = b.c

4. h² = b′.c'

5. 

Trong đó:

• a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;
• b’ là đường chiếu của cạnh b trên cạnh huyền;
• c’ là đường chiếu của cạnh c trên cạnh huyền;
• h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.

d. Công thức tính đường cao trong tam giác cân

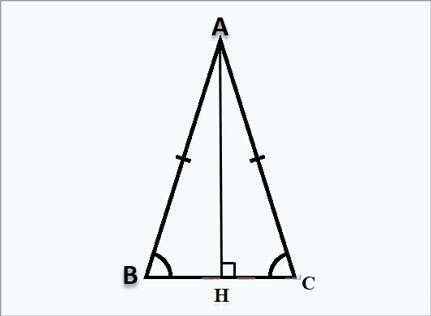
Giả sử các bạn có tam giác ABC cân tại A, đường cao AH vuông góc tại H như hình trên:

Công thức tính đường cao AH:

Vì tam giác ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến nên:

⇒ HB=HC= ½BC

Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:

AH²+BH²=AB²

⇒AH²=AB²−BH²

B. Bài tập Đường cao

1. Bài tập vận dụng

Dạng 1: Hệ thức về cạnh và đường cao trong tam giác vuông

Ví dụ 1: Cho tam giác ABC vuông tại A, chiều cao AH và AB = 5; AC = 12. Đặt BC = y, AH = x. Tính x, y.

Hướng dẫn giải:

Tam giác ABC vuông tại A.

Áp dụng định lí Pytago: BC² = AC² + AB² = 12² + 5² = 169.

Suy ra BC = $\sqrt{169}$ = 13

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông, ta có:

 AB.AC = BC.AH $\Rightarrow AH=\frac{AB.AC}{BC}=\frac{5.12}{13}=\frac{60}{13}$

Vậy $AH=x=\frac{60}{13}$; BC = y = 13.

Ví dụ 2: Cho tam giác vuông có các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền.

Hướng dẫn giải:

Giả sử tam giác ABC vuông tại A với AB = 24 và AC = 7.

Kẻ đường cao AD ứng với cạnh huyền

Áp dụng định lí Pytago: BC² = AC² + AB² = 7² + 24² = 625.

Suy ra BC = $\sqrt{625}$ = 25

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông, ta có:

AC² = CD.BC $\Rightarrow CD=\frac{A{C}^2}{BC}=\frac{7^2}{25}=1,96$

Nên BD = BC – CD = 25 – 1,96 = 23,04.

 Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông, ta có:

AD² = BD.CD  Suy ra $AD=\sqrt{BC.CD}=\sqrt{23,04.1,96}=6,72.$

Dạng 2: Tính chất ba đường cao trong tam giác

Bài 1: Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em hãy chọn phát biểu đúng:

A. H là trọng tâm của ΔABC

B. H là tâm đường tròn nội tiếp ΔABC

C. CH là đường cao của ΔABC

D. CH là đường trung trực của ΔABC

Lời giải:

Vì hai đường cao AM và BN cắt nhau tại H nên CH là đường cao của ΔABC và H là trực tâm tam giác ΔABC nên A, B, D sai, C đúng.

Chọn đáp án C

Bài 2: Cho ΔABC cân tại A có AM là đường trung tuyến khi đó

A. AM ⊥ BC

B. AM là đường trung trực của BC

C. AM là đường phân giác của góc BAC

D. Cả A, B, C đều đúng

Lời giải:

Vì ΔABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC

Chọn đáp án D

Bài 3: Cho ΔABC cân tại A, trung tuyến AM. Biết BC = 24cm, AM = 5cm. Tính độ dài các cạnh AB và AC

A. AB = AC = 13cm

B. AB = AC = 14cm

C. AB = AC = 15cm

D. AB = AC = 16cm

Lời giải:

ΔABC cân tại A (gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó.

Vì AM là trung tuyến của ΔABC nên M là trung điểm của BC

Bài 4: Đường cao của tam giác đều cạnh a có bình phương độ dài là

Lời giải:

Xét tam giác ABC đều cạnh AB = AC = BC = a có AM là đường trung tuyến suy ra AM cũng là đường cao của tam giác ABC hay AM ⊥ BC tại M

Vậy bình phương độ dài đường cao của tam giác đều cạnh a là (3a²)/4

Chọn đáp án A

Bài 5: Cho ΔABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng

A. AI > AK                B. AI < AK               C. AI = 2AK               D. AI = AK

Lời giải:

Chọn đáp án D

Bài 6: Cho ΔABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC . Trên tia đối của tia CE lấy điểm K sao cho CK = AB. ΔAIK là tam giác gì?

A. ΔAIK là tam giác cân tại B

B. ΔAIK là tam giác vuông cân tại A

C. ΔAIK là tam giác vuông

D. ΔAIK là tam giác đều

Lời giải:

Chọn đáp án B

Bài 7: Cho tam giác ABC không cân. Khi đó trực tâm của tam giác ABC là giao điểm của:

A. Ba đường trung tuyến

B. Ba đường phân giác

C. Ba đường trung trực

D. Ba đường cao

Lời giải:

Vì tam giác ABC là tam giác không cân nên trực tâm của tam giác ABC là giao điểm của ba đường cao.

Chọn đáp án D

Bài 8: Cho tam giác ABC vuông tại A. Lấy H thuộc AB, vẽ HE ⊥ BC ở E. Tia EH cắt tia CA tại D. Khi đó

A. H là trọng tâm của tam giác BDC

B. H là trực tâm của tam giác BDC

C. H là giao ba đường trung trực của tam giác BDC

D. H là giao ba đường phân giác của tam giác BDC

Lời giải:

Trong tam giác BDC có:

BA ⊥ CD tại A (do tam giác ABC vuông tại A) ⇒ BA là một đường cao của tam giác BDC

DE ⊥ BC tại E (do HE ⊥ BC) ⊥ DE là một đường cao của tam giác BCD

Mà DE ∩ BA = H

Do đó H là giao điểm của hai đường cao trong tam giác BDC

Suy ra H là giao điểm của ba đường cao trong tam giác BDC

Vậy H là trực tâm của tam giác BDC.

Chọn đáp án B

Bài 9: Cho tam giác ABC vuông ở A có đường cao AD. Lấy H thuộc AD và E thuộc CD sao cho HE // AC Khi đó

A. BH ⊥ AE

B. BH // AE

C. AE ⊥ AD

D. BH ⊥ AD

Lời giải:

+ Ta có: HE // AC; AC ⊥ AB (do tam giác ABC vuông tại A)

Suy ra HE ⊥ AB (quan hệ từ vuông góc đến song song)

Trong tam giác ABE có:

AD ⊥ BE tại D nên AD là một đường cao của tam giác ABE

HE ⊥ AB nên E, H thuộc một đường cao của tam giác ABE

Mà H = HE ∩ AD

Do đó H là giao của hai đường cao trong tam giác ABE

Nên H là giao của ba đường cao trong tam giác ABE (ba đường cao của một tam giác đồng quy tại một điểm)

Vậy H là trực tâm của tam giác ABE

Suy ra BH ⊥ AE nên đáp án A đúng, đáp án B sai

+ Vì tia AD và tia AE đều nằm trong góc BAC, mà  nên AD không thể vuông góc với AE, do đó đáp án C sai.

+ Vì BH ⊥ AE mà AE ∩ AD = A nên BH không thể vuông góc với AD nên đáp án D sai.

Chọn đáp án A

Bài 10: Cho tam giác ABC có góc $\hat{C}$ = 45°, độ dài đường cao AH bằng 12cm và diện tích bằng 120cm². Tính độ dài BH.

A. 8cm

B. 12cm

C. 15cm

D. 17cm

Lời giải:

Chọn đáp án A

2. Bài tập tự luyện 

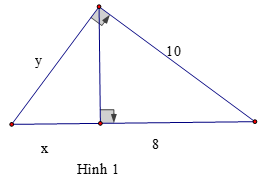
Bài 1: Tính x, y trong mỗi hình sau:

Bài 2: Cho tam giác ABC vuông tại A, AB : AC = 7 : 24, BC = 625 cm. Tính độ dài hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 20 cm, BH = 9cm. Tính độ dài BC và AH

Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC

Bài 5: Cho tam giác ABC vuông tại A, đường cao AH

    Cho biết AC/AB = √2; HC - HB = 2cm.Tính:

    a) Tỉ số HC : HB

    b) Các cạnh của tam giác ABC

Bài 6: Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Trên HB, HC lần lượt lấy các điểm M, N sao cho góc AMC bằng góc ANB bằng 90⁰. Chứng minh rằng AM = AN

Bài 7: Cho tam giác ABC đường cao AH. Vẽ HD ⊥ AB. Tia phân giác của góc AHC cắt AC tại F. Biết AB = 6cm, AC = 8cm, BC = 10 cm. Tính:

    a) Độ dài AH

    b) Chu vi tam giác ADF

Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng 

Bài 9: Cho tam giác ABC vuông tại A có diện tích S không đổi. Gọi p là chu vi của nó. Tìm giá trị nhỏ nhất của p.