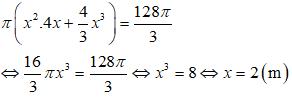Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Công thức tính Thể tích khối cầu và bài tập vận dụng, tài liệu bao gồm lý thuyết và đầy đủ các dạng bài tập, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Công thức tính Thể tích khối cầu và bài tập vận dụng
1. Định nghĩa khối cầu
Khối cầu được tạo bởi toàn bộ không gian từ mặt cầu đến tâm của nó.
Thể tích khối cầu được hiểu là tất cả phần không gian của khối cầu hoặc phần không gian ở phía bên trong của mặt cầu.
2. Công thức tính thể tích khối cầu
Để có thể tính được thể tích khối cầu ta cần tìm kích thước bán kính của nó. Sau đó thay vào công thức
V = π.r3 để tính. Thể tích có đơn vị khối (cm3, m3,…)
• V là thể tích của khối cầu có đơn vị m3
• π là số pi, có giá trị xấp xỉ 3,14
• r là bán kính của khối cầu
• d là bánh kính mặt cầu hoặc hình cầu
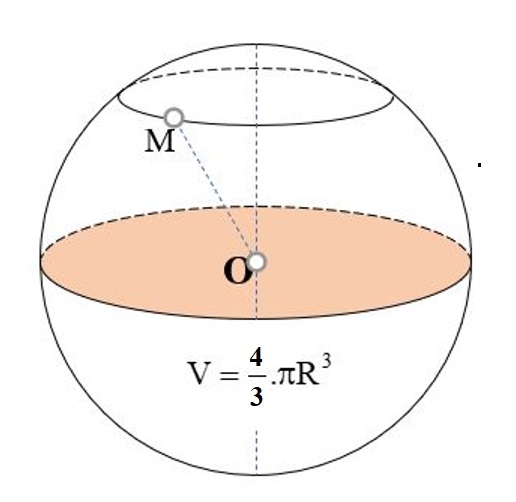
Các bạn cần thực hiện qua 3 bước sau đây để có thể giải một bài toán tính thể tích khối cầu (hình cầu).
• Bước 1: Sử dụng giấy nháp và viết công thức tính thể tích hình cầu.
V = π.r3
• Bước 2: Tìm kích thước bán kính
Nếu đề bài toán có cho sẵn kích thước bán kính ⇒ Thực hiện bước tiếp theo.
Nếu đề bài cho đường kính thì cần thực hiện chia đôi để có được bán kính (r). Ví dụ, đường kính d = 20 cm, thì bán kính r = 10 cm.
• Bước 3: Sử dụng công thức tính thể tích hình cầu và thay vào đề bài.
Ví dụ: Tìm được bán kính khối cầu r = 10 cm. Ta có,
Thể tích khối cầu V = π.r3 = .π.(10)³ = π cm³
• Mọi điểm cách đều hai đầu mút của đoạn thẳng thì nằm trên mặt phẳng trung trực của đoạn thẳng và ngược lại.
5. Bài tập vận dụng
Bài 1. Mặt cầu có bán kính R√3 có diện tích là:
A. 4√3πR2 . B. 4πR2 . C. 6πR2 . D. 12πR2 .
Hướng dẫn giải:
Áp dụng công thức: S = 4πR2
Diện tích mặt cầu có bán kính R√3 là:
S = 4π(R√3)2 = 12πR2 .
Chọn D.
Bài 2. Cho hình tròn đường kính 4a quay quanh đường kính của nó. Khi đó thể tích khối tròn xoay sinh ra bằng:
A. 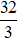
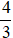

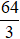
Hướng dẫn giải:
Cho hình tròn đường kính 4a quay quanh đường kính của nó ta được khối cầu có đường kính 4a hay bán kính R = 2a.
Thể tích khối cầu là:
V = 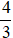
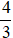
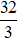
Chọn A
Bài 3. Khối cầu ( S) có diện tích mặt cầu bằng (đvdt). Tính thể tích khối cầu.
A. 

C. 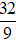
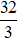
Hướng dẫn giải:
Do khối cầu (S) có diện tích mặt cầu bằng nên ta có:
S = 4πR2 = 16π ⇒ R = 2
Thể tích của khối cầu là:
V = 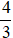
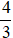
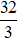
Chọn D.
Bài 4. Cho khối cầu có thể tích là 36π (cm3) . Bán kính R của khối cầu là:
A. R = 6 cm B. R= 3 cm.
C. R = 3√2 cm D. R = √6 cm
Hướng dẫn giải:
Thể tích của khối cầu V = 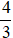
⇒ R3 = 27 ⇔ R = 3 cm.
Chọn B.
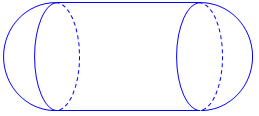
Bài 5. Một cái bồn chứa nước gồm hai nửa hình cầu và một hình trụ (như hình vẽ).
Đường sinh của hình trụ bằng hai lần đường kính của hình cầu. Biết thể tích của bồn chứa nước là 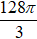
A. 50π(m2) B. 64π(m2)
C. 40π(m2) D. 48π(m2)
Hướng dẫn giải:
Gọi 4x ( m) là đường sinh hình trụ.
Khi đó đường tròn đáy hình trụ và mặt cầu có bán kính là x (m).
Thể tích bồn chứa nước này chính là thể tích của khối trụ có bán kính đáy R = x;
đường sinh l = h = 4x và thể tích khối cầu có bán kính R= x.
Do đó, thể tích bồn chứa nước là:
Vậy diện tích xung quanh bồn nước là:
π(4x2 + 2.x.4x) = 48π(m2) .
Chọn D.
Xem thêm các nội dung khác: