Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng

Quý Lê Xuân Ngày: 08-03-2024 Tổng hợp kiến thức

Tải xuống 37 7.9 K 76

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập bộ bài tập Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng, tài liệu tuyển chọn bài tập Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng có phương pháp giải chi tiết và bài tập có đáp án (có lời giải), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng

1. Định nghĩa

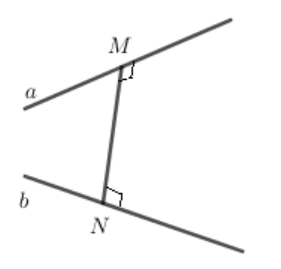
- Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đianj vuông góc chung của hai đường thẳng đó.

Kí hiệu: d (a,b) = MN trong đó M $\in$ a, N $\in$ b và MN $⊥$ a, MN $⊥$ b

Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng (ảnh 1)

+ Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó mà chứa đường thẳng còn lại.

+Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó

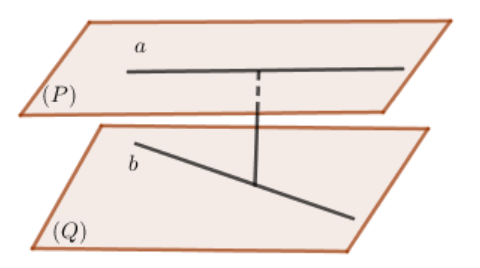
Cách tính Khoảng cách giữa 2 đường thẳng chéo nhau và bài tập vận dụng (ảnh 3)

Kí hiệu: d(a,b) = d(a,(Q)) = d(b,(P)) = d ((P),(Q)) trong đó (P), (Q) là hai mặt phẳng lần lượt chứa các đường thẳng a, b và (P)//(Q)

2. Phương pháp xác định khoảng cách:

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau:

 Dựng đoạn vuông góc chung MN của a và b. Khi đó

$d (a, b) = M N$ . Sau đây là một số cách dựng đoạn vuông góc chung thường dùng :

Phương pháp 1:

Chọn mặt phẳng $(α)$ chứa đường thẳng $Δ$ và song song với $Δ'$ . Khi đó $d (Δ, Δ') = d (Δ', (α))$

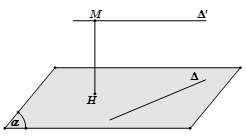
Cách tính khoảng cách giữa hai đường thẳng chéo nhau (ảnh 2)

Phương pháp 2:

Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

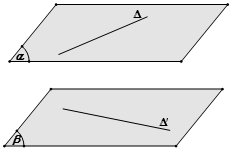
Cách tính khoảng cách giữa hai đường thẳng chéo nhau (ảnh 3)

Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.

Trường hợp 1: $Δ$ và $Δ'$ vừa chéo nhau vừa vuông góc với nhau

Bước 1: Chọn mặt phẳng $(α)$ chứa $Δ'$ và vuông góc với $Δ$ tại $I$ .

Bước 2: Trong mặt phẳng $(α)$ kẻ $I J ⊥ Δ'$ .

Khi đó $I J$ là đoạn vuông góc chung và $d (Δ, Δ') = I J$ .

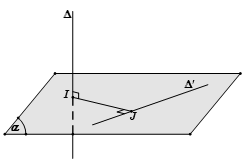
Cách tính khoảng cách giữa hai đường thẳng chéo nhau (ảnh 4)

Trường hợp 2: $Δ$ và $Δ'$ chéo nhau mà không vuông góc với nhau

Bước 1: Chọn mặt phẳng $(α)$ chứa $Δ'$ và song song với $Δ$ .

Bước 2: Dựng d là hình chiếu vuông góc của $Δ$ xuống $(α)$ bằng cách lấy điểm $M \in Δ$ dựng đoạn $M N ⊥ (α)$ , lúc đó d là đường thẳng đi qua N và song song với $Δ$ .

Bước 3: Gọi $H = d \cap Δ'$ , dựng $H K ∥ M N$

Khi đó $H K$ là đoạn vuông góc chung và $d (Δ, Δ') = H K = M N$ .

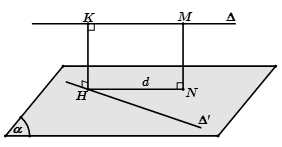
Cách tính khoảng cách giữa hai đường thẳng chéo nhau (ảnh 5)

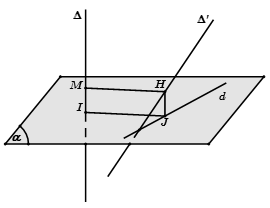
Hoặc

Bước 1: Chọn mặt phẳng $(α) ⊥ Δ$ tại I.

Bước 2: Tìm hình chiếu d của $Δ'$ xuống mặt phẳng $(α)$ .

Bước 3: Trong mặt phẳng $(α)$ , dựng $I J ⊥ d$ , từ J dựng đường thẳng song song với $Δ$ cắt $Δ'$ tại H, từ H dựng $H M ∥ I J$ .

Khi đó $H M$ là đoạn vuông góc chung và $d (Δ, Δ') = H M = I J$ .

Cách tính khoảng cách giữa hai đường thẳng chéo nhau (ảnh 6)

Phương pháp 4: Sử dụng phương pháp vec tơ

a) MN là đoạn vuông góc chung của AB và CD khi và chỉ khi $\{\begin{cases} \vec{A M} = x \vec{A B} \\ \vec{C N} = y \vec{C D} \\ \vec{M N} . \vec{A B} = 0 \\ \vec{M N} . \vec{C D} = 0 \end{cases}$

b) Nếu trong $(α)$ có hai vec tơ không cùng phương $\vec{u_{1}}, \vec{u_{2}}$ thì $O H = d (O, (α)) \Leftrightarrow \{\begin{cases} \vec{O H} ⊥ \vec{u_{1}} \\ \vec{O H} ⊥ \vec{u_{2}} \\ H \in (α) \end{cases}$ $\Leftrightarrow \{\begin{cases} \vec{O H} . \vec{u_{1}} = 0 \\ \vec{O H} . \vec{u_{2}} = 0 \\ H \in (α) \end{cases}$ .

3. Bài tập tự luyện

Bài 1: Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa AB và CD.

Hướng dẫn giải

Chọn C

Gọi M và N lần lượt là trung điểm của AB và CD

+ Xét tam giác ACD đều có NA là đường trung tuyến đồng thời là đường cao nên NA = (a√3)/2.

Tương tự: NB = (a√3)/2.

⇒ NA = NB nên tam giác ANB cân tại N

suy ra đường trung tuyến NM đồng thời là đường cao: NM ⊥ AB

+ Chứng minh tương tự ta có NM ⊥ DC, nên d(AB; CD) = MN.

Bài 2: Cho hình chóp S.ABCD có mặt đáy là hình thoi tâm O, cạnh a và ∠BAD = 60° và SO = 3a/4. Biết SA = SC và SB = SD. Hỏi khoảng cách giữa SA và BD bằng bao nhiêu ?

Hướng dẫn giải

+ Vì SA = SC nên tam giác SAC cân tại S ⇒ SO ⊥ AC

Vì SB = SD nên tam giác SBD cân tại S ⇒ SO ⊥ BD.

+ Ta có:

Trong mp(SAC) , kẻ OH ⊥ SA (H ∈ SA). Ta chứng minh OH là đoạn vuông góc chung của SA và BD

Ta có: OH ⊥ SA (cách dựng) và OH ⊥BD ( vì BD⊥( SAC)

⇒ OH là đoạn vuông góc chung của SA và BD. Do đó: d(SA; DB) = OH.

Ta có: Tam giác ABD cân tại A có góc A bằng 60° nên tam giác ABD đều cạnh a.

+ Tam giác SOA vuông tại O, có OH là đường cao, ta có:

Chọn B

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AC = a√5; BC = a√2. Đường thẳng SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa SD và BC

Hướng dẫn giải

Ta tìm đoạn vuông góc chung của SD và BC:

Lại có; DC ⊥ BC nên DC là đoạn vuông góc chung của SD và BC

⇒ d(SD; BC) = DC.

Áp dụng định lí Pyta go vào tam giác vuông ABC có

Chọn đáp án D

Bài 4: Cho tứ diện đều ABCD cạnh a. Khoảng cách giữa hai đường thẳng AB và CD bằng bao nhiêu?

Hướng dẫn giải

Gọi M; N lần lượt là trung điểm các cạnh CD và AB.

Ta chứng minh MN là đoạn vuông góc chung của AB và CD.

+ Do ABCD là tứ diện đều nên ΔACD = ΔBCD

⇒ AM = BM

⇒ Tam giác MAB cân tại M có MN là đường trung tuyến nên đồng thời là đường cao.

⇒ MN ⊥ AB

+ Chứng minh tương tự ta có: MN ⊥ CD

⇒ MN là đoạn vuông góc chung của AB và CD.

⇒ d( AB; CD) = MN

+ Ta có: NB = AB/2 = a/2.

Tam giác BCD đều cạnh a nên BM = BC.sin60° = (a√3)/2

Chọn đáp án B

Bài 5: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a và AC = 2a. Tính khoảng cách giữa AC’ và CD’

Hướng dẫn giải

Ta có hình chiếu của AC’ trên mặt phẳng (DCC’D’) là DC' ⊥ D’C nên AC’ ⊥ D'C

⇒ D’C ⊥ (ADC’B’) tại điểm H là trung điểm CD’.

Từ H ta kẻ HK ⊥ AC’

⇒ d(AC’; D’C) = HK (khi đó HK là đoạn vuông góc chung của AC’ và D’C)

Ta tính khoảng cách d từ điểm D đến đường thẳng AC’

+ Áp dụng định li Pytago với tam giác vuông ABC ta có

+ Áp dụng định lí pytago với tam giác vuông DCC’ ta có:

+ Xét tam giác ADC’ có:

Chọn đáp án D

Bài 6: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có AB = a, $B C = a \sqrt{3}$ . Biết $S A = \frac{a}{\sqrt{2}}$

a) Tính khoảng cách giữa hai đường thẳng SB và AC

b) Tính khoảng cách giữa hai đường thẳng SC và AB.

Hướng dẫn giải

a) Dựng $B x / / A C, A E ⊥ B x \Rightarrow (S A E) ⊥ B x$

Dựng $A F ⊥ S E \Rightarrow d (A C; S B) = A F$

Dựng $B H ⊥ A C$ dễ thấy $A E = B H = \frac{a \sqrt{3}}{2}$

Ta có: $A F = \frac{A E . S A}{\sqrt{S A^{2} + A E^{2}}} = \frac{a \sqrt{30}}{10}$

b) Dựng $C y / / A B \Rightarrow d (A B, S C) = d (A B, (S C y))$

Dựng $C y / / A B \Rightarrow d (A B, S C) = d (A B, (S C y))$

Lại có : $A M = B C = a \sqrt{3} \Rightarrow A N = \frac{A M . S A}{\sqrt{S A^{2} + A M^{2}}} = \frac{a \sqrt{21}}{27}$

N NHỚ
hình chiếu vuông góc của nó lên mặt phẳng đó.d (M, (α)) = M M ′ với M ′ là hình chiếu

Tài liệu có 37 trang. Để xem toàn bộ tài liệu, vui lòng tải xuống

Từ khóa :

Toán 11 khoảng cách giữa hai đường thẳng chéo nhau và vuông góc với nhau mặt phẳng trong không gian

Đánh giá

0 đánh giá

Đánh giá

Tìm kiếm