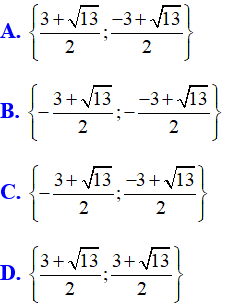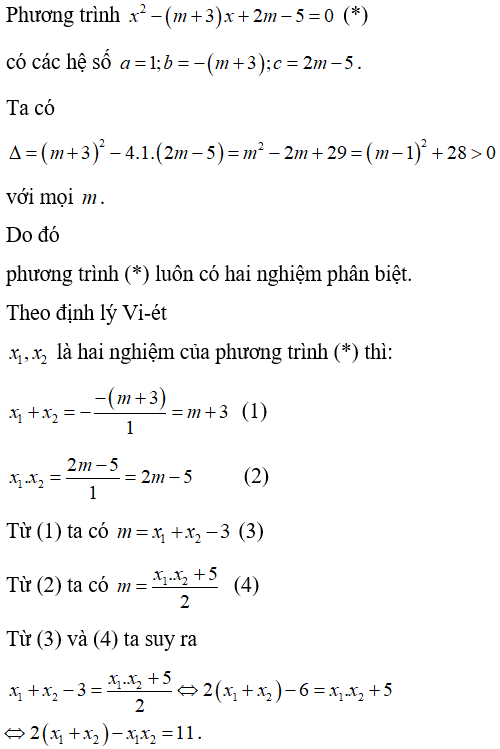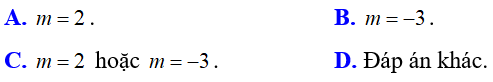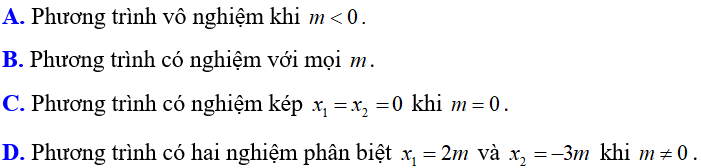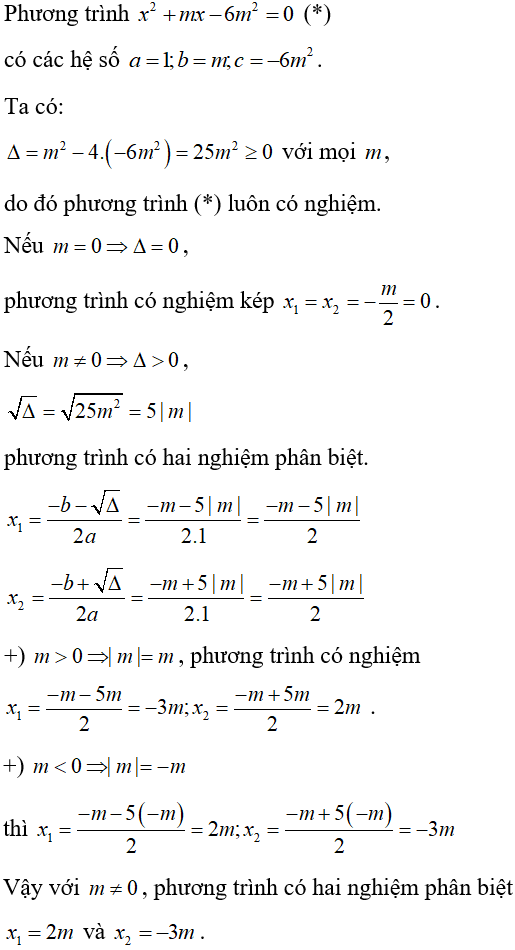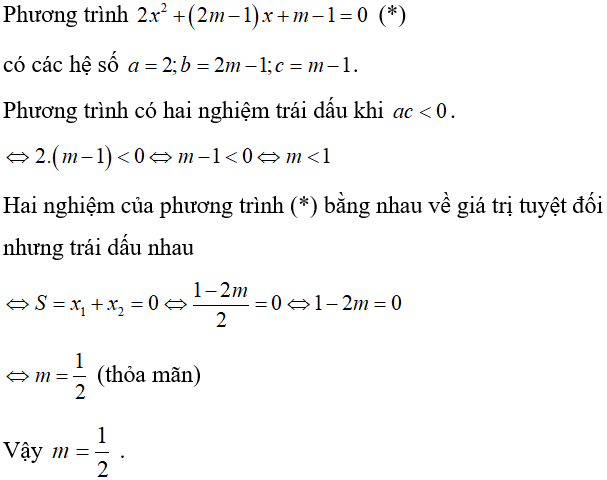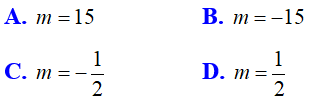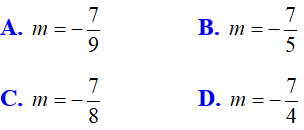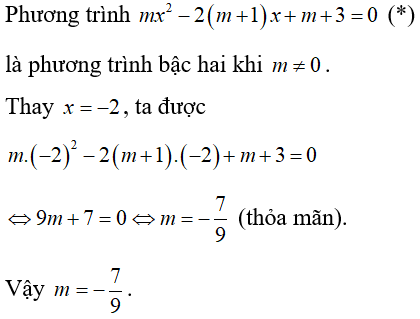Tailieumoi.vn xin giới thiếu tới bạn đọc tài liệu về Nghiệm kép là gì? 50 Bài tập về phương trình có nghiệm kép, chi tiết nhất, tài liệu gồm đầy đủ về lý thuyết Nghiệm kép, các dạng bài tập và ví dụ minh họa, giúp các bạn củng cố kiến thức, học tốt môn Toán hơn.
Nghiệm kép là gì? 50 Bài tập về phương trình có nghiệm kép
A. Lý thuyết Nghiệm kép
Phương trình có nghiệm kép là phương trình bậc 2 mà có hai nghiệm gần như nhau. Để xác định một phương trình có nghiệm kép, ta cần tính giá trị của được tính bằng công thức
Nếu giá trị của là 0 tức là
= 0 thì phương trình có nghiệm kép
Công thức tính nghiệm kép của phương trình là x =
Phương trình có nghiệm kép khi:
Để phương trình bậc 2 có nghiệm kép thì cần đảm bảo những điều kiện sau:
- Hệ số a của phương trình phải khác 0 tức là phương trình không được là phương trình bậc 1
- của phương trình phải bằng 0.
được tính theo công thức
trong đó có a, b, c là các hệ số của phương trình
Nếu bằng 0 thì phương trình có nghiệm kép
Nếu khác 0 thì phương trình không có nghiệm kép
Ví dụ: Để phương trình ax + bx + c = 0 có nghiệm kép thì ta cần thực hiện các bước sau:
- kiểm tra hệ số a của phương trình: Nếu a = 0 tức là phương trình không phải là phương trình bậc 2 và không có nghiệm kép
- Tính giá trị của bằng cách sử dụng công thức
= b
- 4ac với a,b, c lần lượt là các hệ số phương trình
B. Bài tập phương trình nghiệm kép
Ví dụ 1: Tập nghiệm của phương trình x2 + 3x - 1 = 0 là:
Lời giải
Chọn C
Ví dụ 2: Giá trị nào sau đây là nghiệm của phương trình 3x2 + 7x + 2 = 0
Lời giải
Chọn B
Ví dụ 3: Phương trình x2 - 2mx + m = 0 với m = 1 có tập nghiệm là:
Lời giải
Chọn C
Ví dụ 4: Cho phương trình bậc hai (m - 1)x2 - 2mx + m + 1 = 0 (m là tham số). Các giá trị nguyên của m để phương trình có nghiệm nguyên là:
Lời giải
Chọn A
Ví dụ 5: Phương trình x2 + (2m + 1)x + 3m = 0 (với m là tham số) có hai nghiệm phân biệt, trong đó có một nghiệm là x1 = 3, nghiệm còn lại là x2 bằng:
Lời giải
Chọn D
Ví dụ 6: Tìm hệ thức liên hệ giữa hai nghiệm của phương trình x2 - (m + 3)x + 2m - 5 = 0 không phụ thuộc vào m.
Lời giải
Chọn A
Ví dụ 7: Cho phương trình x2 - 2x - 8 = 0 có hai nghiệm x1 và x2. Phương trình bậc hai một ẩn có hai nghiệm là y1 = x1 - 3 và y2 = x2 - 3 là:
Lời giải
Chọn C
Ví dụ 8: Giải phương trình x2 - 2x + 1 - m2 = 0 với m là tham số, m ≠ 0.
Lời giải
Chọn A
Ví dụ 9: Cho phương trình x2 + √7x + 1 = 0. Khẳng định nào sau đây là đúng?
Lời giải
Chọn B
Ví dụ 10: Số các giá trị nguyên của tham số m để phương trình x2 - 2x + m = 0 có hai nghiệm phân biệt x1; x2 sao cho x12.x22 ≤ 4 là:.
Lời giải
Chọn B
Ví dụ 11: Phương trình bậc hai mx2 + (2m + 1)x + 3 = 0 có một nghiệm là x = -1. Giá trị của m và nghiệm còn lại là:
Lời giải
Chọn A
Ví dụ 12: Cho hai phương trình bậc hai x2 + 2x + m = 0 (1) và x2 + mx + 2 = 0 (2) (với m là tham số). Tìm m để hai phương trình có ít nhất một nghiệm chung.
Lời giải
Chọn B
Ví dụ 13: Cho phương trình x2 + mx - 6m2 = 0 với m là tham số. Chọn khẳng định sai:
Lời giải
Chọn A
Ví dụ 14: Cho phương trình mx2 - 2(m + 1)x + m + 2 = 0. Chọn kết luận đúng.
Lời giải
Chọn B
Ví dụ 15: Khi phương trình x2 + (m + 1)x - m = 0 có nghiệm kép, giá trị của nghiệm kép là:
Lời giải
Chọn C
Ví dụ 16: Cho phương trình x2 - 2x + 1 - m2 = 0 với m là tham số. Khẳng định nào sau đây là đúng?
Lời giải
Chọn D
Ví dụ 17: Giá trị nguyên nhỏ nhất của tham số m để phương trình x2 - 2(m + 7)x + m2 - 4 = 0 có hai nghiệm trái dấu là:
Lời giải
Chọn C
Ví dụ 18: Phương trình 2x2 + (2m - 1)x + m - 1 = 0 có hai nghiệm bằng nhau về giá trị tuyệt đối nhưng trái dấu nhau khi:
Lời giải
Chọn C
Ví dụ 19: Tìm m để phương trình x2 - 2(m - 2)x - 6m = 0 có nghiệm x1; x2 sao cho biểu thức x12 + x22 đạt giá trị nhỏ nhất.
Lời giải
Chọn D
Ví dụ 20:Tìm m để mx2 - 2(m + 1)x + m + 3 = 0 là phương trình bậc hai nhận x = -2 là nghiệm.
Lời giải
Chọn A
Ví dụ 21: Tìm m để hai phương trình x2 + x + m - 2 = 0 (1) và x2 + (m - 2)x + 1 = 0 (2) có nghiệm chung.
Lời giải
Chọn D
Xem thêm các nội dung khác: