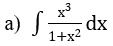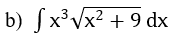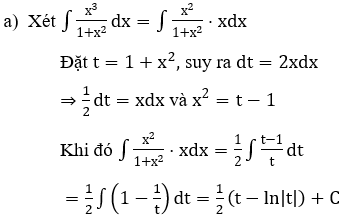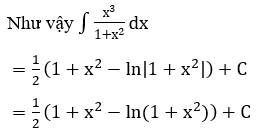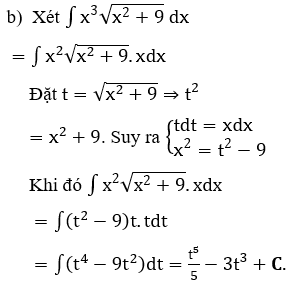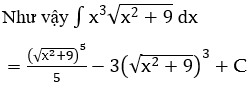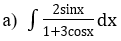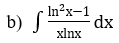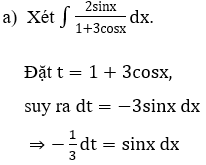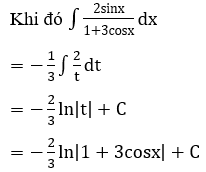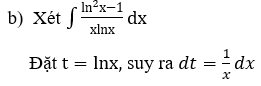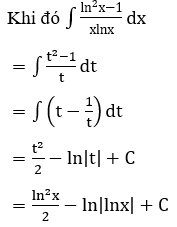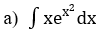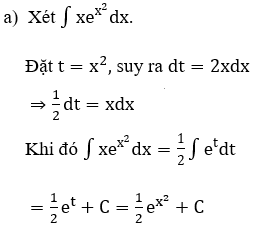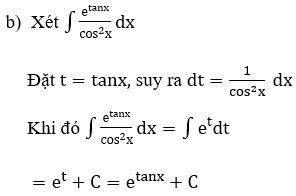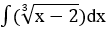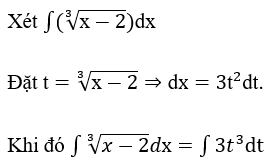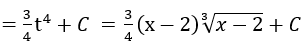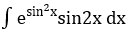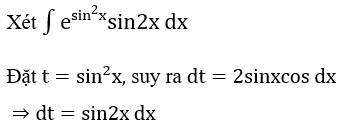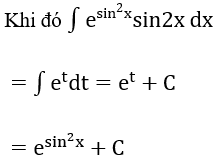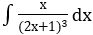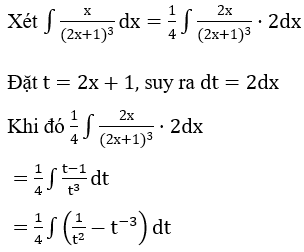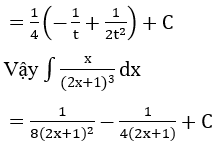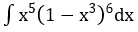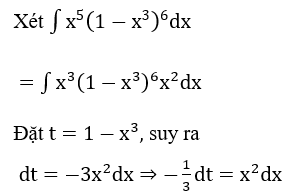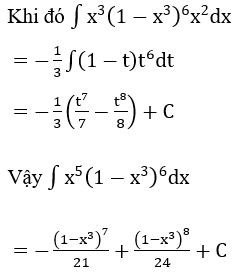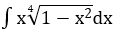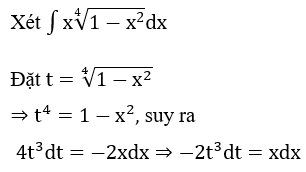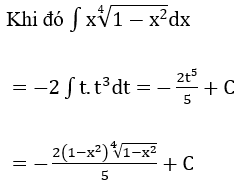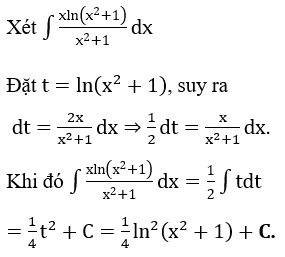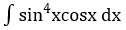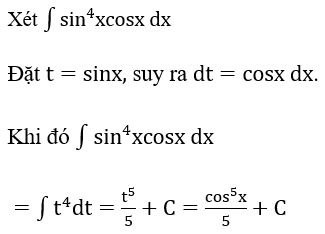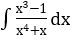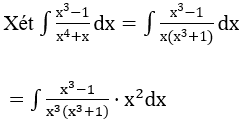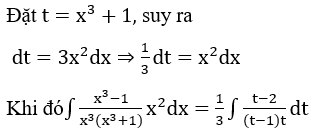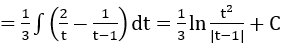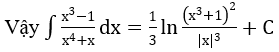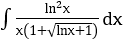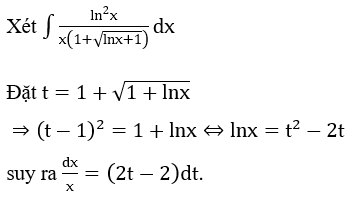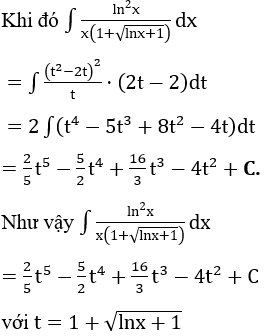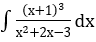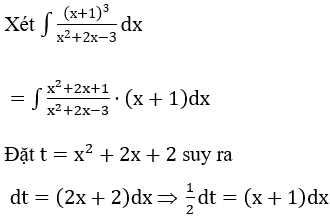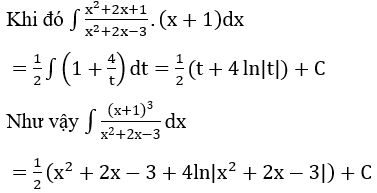Bài viết Tìm nguyên hàm bằng phương pháp đổi biến số với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Tìm nguyên hàm bằng phương pháp đổi biến số.
Tìm nguyên hàm bằng phương pháp đổi biến số cực hay
A. Phương pháp giải & Ví dụ
| STT | Dạng tích phân | Cách đặt | Đặc điểm nhận dạng |
| 1 | 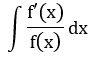 |
t = f(x) | Biểu thức dưới mẫu |
| 2 |  |
t = t(x) | Biểu thức ở phần số mũ |
| 3 | 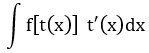 |
t = t(x) | Biểu thức trong dấu ngoặc |
| 4 | 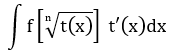 |
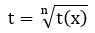 |
Căn thức |
| 5 | 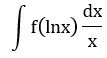 |
t = lnx | dx/x đi kèm biểu thức theo lnx |
| 6 | 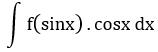 |
t = sinx | cosx dx đi kèm biểu thức theo sinx |
| 7 | 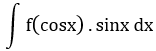 |
t = cosx | sinx dx đi kèm biểu thức theo cosx |
| 8 | 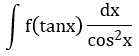 |
t = tanx | 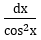 đi kèm biểu thức theo tanx đi kèm biểu thức theo tanx |
| 9 | 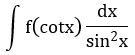 |
t = cotx | 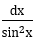 đi kèm biểu thức theo cotx đi kèm biểu thức theo cotx |
| 10 | 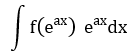 |
t = eax | eax dx đi kèm biểu thức theo eax |
| Đôi khi thay cách đặt t = t(x) bởi t = m.t(x) + n ta sẽ biến đổi dễ dàng hơn. | |||
Ví dụ minh họa
Bài 1: Tìm các họ nguyên hàm sau đây:
Lời giải:
Bài 2: Tìm các họ nguyên hàm sau đây:
Lời giải:
Bài 3: Tìm các họ nguyên hàm sau đây:
Lời giải:
B. Bài tập vận dụng
Bài 1: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 2: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 3: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 4: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 5: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 6: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 7: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 8: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 9: Tìm họ nguyên hàm của hàm số
Lời giải:
Bài 10: Tìm họ nguyên hàm của hàm số
Lời giải:
Xem thêm các nội dung khác: