Cho tam giác nhọn ABC có trực tâm H và = 60°. Gọi M, N, P theo thứ tự là chân các đường cao kẻ từ các đỉnh A, B, C

Cho tam giác nhọn ABC có trực tâm H và = 60°. Gọi M, N, P theo thứ tự là chân các đường cao kẻ từ các đỉnh A, B, C

Nguyễn Mạnh Tài Ngày: 09-03-2024 Tổng hợp kiến thức

114

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 88)

Đề bài. Cho tam giác nhọn ABC có trực tâm H và = 60°. Gọi M, N, P theo thứ tự là chân các đường cao kẻ từ các đỉnh A, B, C của tam giác ABC và I là trung điểm của BC. Chứng minh rằng tam giác INP đều.

Lời giải:

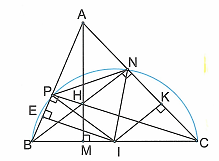
15000 câu hỏi ôn tập môn Toán có đáp án (Phần 98) (ảnh 1)

Ta thấy ΔBNC và ΔBPC là hai tam giác vuông có chung cạnh huyền BC nên bốn điểm B, P, N, C nằm trên đường tròn tâm I, đường kính BC.

Khi đó IN = IP ⇒ ΔINP cân tại I (1)

Tam giác ABN vuông tại N có: $\hat{A B N} + \hat{B A N} = 90 °$

⇒ $\hat{A B N} = 90 ° - \hat{B A N} = 90 ° - 60 ° = 30 °$

Ta có $\hat{P B N}$ là góc nội tiếp và $\hat{P I N}$ là góc ở tâm cùng chắn cung $\overset{⏜}{N P}$

Do đó $\hat{P I N} = 2 \hat{P B N} = 60 °$ (2)

Từ (1) và (2) suy ra ΔINP đều.

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Xét xem dãy u_n = 3n – 1 có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.

Đề bài. Một vé xem phim có mức giá là 60000 đồng. Trong dịp khuyến mãi cuối năm 2018, số lượng người xem phim tăng lên 45% nên tổng doanh thu cũng tăng 8,75%. Hỏi rạp phim đã giảm giá mỗi vé bao nhiêu % so với giá bán ban đầu?

Đề bài. Tính giá trị của biểu thức: P = (x – 10)² – x(x + 80) tại x = 0,87.

Đề bài. Tính giá trị biểu thức A = 100 – 99 + 98 – 97 + … + 4 – 3 + 2.

Đề bài. Cho a, b thuộc ℕ và (11a + 2b) chia hết cho 12. Chứng minh rằng: (a + 34b) chia hết cho 12.

Đề bài. Giải phương trình: $\cos (x + \frac{π}{3}) = \cos 2 x$ .

Đề bài. Phân tích đa thức thành nhân tử: 8(x + y + z)³ – (x + y)³ – (y + z)³ – (z + x)³.

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC.

2

Đề bài 1. Tìm m để hai đường thẳng (d₁) y = mx + 5 – m và (d₂) y = 3x + m – 1 cắt nhau tại một điểm nằm trên trục tung.

Đề bài 2. Tìm m để 2 đường thẳng (d) cắt nhau tại 1 điểm trên trục tung cho hàm số y = (m + 2)x + 2m² + 1 tìm m để hai đường thẳng (d): y = (m + 2)x + 2m² + 1 và (d'): y = 3x + 3 cắt nhau tại 1 điểm trên trục tung.

Đề bài. Tìm m để phương trình x² – (3m – 1)x + 2m² – m = 0 có nghiệm phân biệt x₁, x₂ thỏa mãn x₁ = x₂².

Đề bài. Tính giá trị biểu thức: $- \frac{5}{12} + 1 + \frac{5}{18} - 2, 25$ .

Đề bài. Cho tam giác ABC vuông tại A (AB > AC) có đường cao AH. Gọi AD là phân giác của HAB.

Đề bài. Rút gọn biểu thức: $\frac{x^{2}}{5 x + 25} + \frac{2 x - 10}{x} + \frac{50 + 5 x}{x^{2} + 5 x}$ .

Đề bài. Cho tam giác ABC có $\hat{B} = \hat{C}$ , gọi H là trung điểm BC. Chứng minh AH là phân giác góc $\hat{A}$ .

Đề bài. Tính 30% của 70.

Đề bài. Trên mặt phẳng Oxy, cho đường thẳng (d): y = ax + b với a, b là hằng số. Tìm a, b biết: d đi qua điểm M(1; −2) và song song với đường thẳng d₁: y = 2x – 1.

Đề bài. Cho hình bình hành ABCD và O là giao điểm của AC và BD. Trên đường chéo AC lấy 2 điểm M và N sao cho AM = MN = NC

Đề bài. Cho a, b, m là các số tự nhiên khác 0. Biết (7a + b) chia hết cho m và (8a + b) chia hết cho m. Chứng minh rằng b cũng chia hết cho m.

Đề bài. Cho A là một số lẻ không tận cùng bằng 5. Chứng minh rằng tồn tại một bội của A gồm toàn chữ số 9.

Đề bài. Chứng minh rằng 10⁹ + 10⁸ + 10⁷ chia hết cho 5.

Đề bài. Tính tổng F = 1² + 2² + 3² + … + n².

Đề bài. Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Tính số đo góc $\hat{M O N}$ .

Đề bài. Cho a, b là các số nguyên dương và q = $\frac{a^{2} + b^{2}}{a b + 1}$ là số nguyên. Chứng minh rằng q là số chính phương.

Đề bài. Cho hình vuông ABCD cạnh a. Lấy M thuộc AB, N thuộc AD sao cho AM + AN + MN = 2a. Chứng minh $\hat{M C N} = 45 °$ .

Đề bài. Cho hình vuông ABCD tâm O, trên đoạn BC lấy điểm E bất kì, trên tia đối của tia CD lấy điểm F sao cho CE = CF.

Đề bài. Để thành lập các đội tuyển học sinh giỏi khối 9, nhà trường tổ chức thi chọn các môn Toán, Văn và Ngoại ngữ trên tổng số 111 học sinh. Kết quả có: 70 học sinh giỏi Toán, 65 học sinh giỏi Văn và 62 học sinh giỏi Ngoại ngữ. Trong đó, có 49 học sinh giỏi cả 2 môn Văn và Toán, 32 học sinh giỏi cả 2 môn Toán và Ngoại ngữ, 34 học sinh giỏi cả 2 môn Văn và Ngoại ngữ. Hãy xác định số học sinh giỏi cả ba môn Văn, Toán và Ngoại ngữ. Biết rằng có 6 học sinh không đạt yêu cầu cả ba môn.

Đề bài. Giải tam giác vuông là gì?

Đề bài. Cho tam giác ABC có BC = 6, AB = 5, $\vec{B C} . \vec{B A} = 24$ . Tính diện tích tam giác ABC

Đề bài. Cho các số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh

Đề bài. Cho tam giác ABC, kẻ tia phân giác Bx của góc B, Bx cắt tia AC tại M. Từ M kẻ đường thẳng song song với AB, nó cắt BC tại N. Từ N kẻ tia NY // Bx. Chứng minh:

Đề bài. Cho tam giác ABC cân tại A. Gọi I là tâm đường tròn nội tiếp tam giác, K là tâm đường tròn bàng tiếp góc A và O là trung điểm của IK.

Đề bài. Cho tam giác ABC, IG vuông góc với IC trong đó I là tâm đường tròn nội tiếp, G là trọng tâm. Chứng minh $\frac{a + b + c}{3} = \frac{2 a b}{a + b}$ .

Đề bài. Cho tam giác ABC có $\hat{B} = \hat{C} = 40 °$ . Kẻ phân giác BD.

Đề bài. Cho tam giác ABC có . Diện tích tam giác ABC là:

Đề bài. Giải phương trình: x – $\sqrt{x - 1}$ – 3 = 0.

Đề bài. Cho các hàm số y = 3x – 2 (d₁); y = −x + 6 (d₂).

Đề bài. Cho 5 số nguyên dương đôi một phân biệt sao cho mỗi số trong chúng không có ước nguyên tố nào khác 2 và 3. Chứng minh rằng trong năm số đó tồn tại hai số mà tích của chúng là một số chính phương.

Đề bài. Cho tam giác ABC nhọn nội tiếp (O). Kẻ đường cao AD của tam giác ABC, đường kính AK của đường tròn (O). Gọi E và F lần lượt là hình chiếu của B và C trên AK. Gọi M và N lần lượt là trung điểm của BC và AC. Chứng minh: MN ⊥ DF và M là tâm đường tròn ngoại tiếp tam giác DEF.

Đề bài. Giải phương trình: $\sqrt{x^{2} - 2 x + 1} + \sqrt{x^{2} - 4 x + 4} = 3$

Đề bài. Cho tam giác ABC. Chứng minh rằng sinA + sinB + sinC ≤ $\frac{3 \sqrt{3}}{2}$ .

Đề bài. Phân tích số 90 ra thừa số nguyên tố rồi tìm tập hợp các ước của nó.

Đề bài. Biết A = 1.2 + 2.3 + 3.4 + … + 50.51 = 44 200. Tính S = 1² + 2² +… + 50².

Đề bài. Tam giác ABC nội tiếp (O), AD là đường kính của (O). M là trung điểm của của BC, H là trực tâm của tam giác ABC. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC. Chứng minh rằng 4 điểm X, Y, Z, M cùng thuộc 1 đường tròn.

Đề bài. Cho hình trên biết AB // CD, CD // EF. Tính $\hat{A C D}$ và $\hat{A C E}$ .

Đề bài. Tính giá trị: $\frac{1}{6} - 0, 4. \frac{5}{8} + \frac{1}{2}$ .

Đề bài. Góc ở đỉnh của 1 tam giác cân bằng 78 độ, cạnh đáy là 28,5 cm. Tính các cạnh bên và diện tích của tam giác.

Đề bài. Cho phương trình x² + 2(m – 2)x + m² – 4m = 0.

Đề bài. Tìm số tự nhiên X nhỏ nhất có 11 chữ số biết X chia cho 13 dư 3, chia cho 37 dư 3 và chia cho 29 dư 4.

Đề bài. Cho hình bình hành ABCD có AB = 2AD; $\hat{D} = 70 °$ . Vẽ BH vuông góc AD (H ∈ AD). Gọi M, N lần lượt là trung điểm cạnh CD, AB.

Đề bài. Cho tam giác ABC vuông tại A, biết BC = 13cm; AB = 5cm.

Đề bài. Cho tam giác ABD có AB = 15cm, AD = 20cm, BD = 25cm. Vẽ AM vuông góc BD.

Đề bài. 1 thùng rỗng nặng 1 yến. Khi đổ đầy nước thì thùng nước đó nặng 120kg. Hỏi một nửa thùng đó nặng bao nhiêu?

Đề bài. Cho tam giác ABC vuông tại A, Đường cao AH. Biết BC = 8cm, BH = 2cm.

Đề bài. Từ điểm A ở ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến (O) với B, C là các tiếp điểm. Kẻ một đường thẳng d nằm giữa hai tia AB, AO và đi qua A cắt đường tròn (O) tại E, F (E nằm giữa A, F).

Đề bài. Một đu quay ở công viên có bán kính bằng 10m. Tốc độ của đu quay là 3 vòng/phút. Hỏi mất bao lâu để đu quay quay được góc 270°?

Đề bài. Rút gọn biểu thức sau: (3x + 1)² – 2(3x + 1)(3x + 5) + (3x + 5)².

Đề bài. Tìm x biết: (x – 3)(x² + 3x + 9) + x(x + 2)(2 – x) = 1.

Đề bài. Cho hình lăng trụ đứng ABC.A₁B₁C₁có AB = a, AC = 2a, AA₁ = 2a $\sqrt{5}$ và = 120°. Gọi K, I lần lượt là trung điểm của các cạnh CC₁, BB₁. Khoảng cách từ điểm I đến mặt phẳng (A₁BK) bằng bao nhiêu?

Đề bài. Cho tam giác ABC có đường cao AH. Trên AH, lấy các điểm K, I sao cho AK = KI = IH. Qua I, K lần lượt vẽ các đường thẳng EF//BC, MN//BC (E, M thuộc AB, F, N thuộc AC).

Đề bài. Chứng minh rằng tam giác ABC vuông khi $\frac{b}{\cos B} + \frac{c}{\cos C} = \frac{a}{\sin B . \sin C}$ .

Đề bài. Tìm số tự nhiên x khác 0 để: $1 < \frac{x}{5} < \frac{8}{5}$ .

Đề bài. Chứng minh rằng với mọi tam giác ABC ta có: $\sin \frac{A}{2} = \sqrt{\frac{(p - b) (p - c)}{b c}}$ .

Đề bài. Cho A = 2 + 2² + 2³ + … + 2²⁰²⁴. Tìm chữ số tận cùng của A.

Đề bài. Tìm số tự nhiên $\bar{a b c}$ biết 1 + 2 + 3 + … + $\bar{b c} = \bar{a b c}$ .

Đề bài. Cho đường tròn (O, 13cm) và dây AB = 24cm. Trên các tia OA, OB lần lượt lấy M, N sao cho OM = ON = 33,8cm. Chứng minh MN là tiếp tuyến của (O).

Đề bài. Cho hàm số y = f(x) có bảng biến thiên như sau:

Đề bài. Chứng minh rằng biểu thức sau luôn dương với mọi x.

Đề bài. Tìm số nguyên tố p để p + 2, p + 6 và p + 8 đều là số nguyên tố.

Đề bài. Khai triển hằng đẳng thức a⁴ + b⁴.

Đề bài. Cho tam giác nhọn ABC có trực tâm H và = 60°. Gọi M, N, P theo thứ tự là chân các đường cao kẻ từ các đỉnh A, B, C của tam giác ABC và I là trung điểm của BC. Chứng minh rằng tam giác INP đều.

Đề bài. Cho 2 số tự nhiên y > x thỏa mãn (2y − 1)² = (2y − x)(6y + x).

Đề bài. Phân tích đa thức thành nhân tử: 9x² – y² + 4y – 4.

Đề bài. Cho đường thẳng d: y = (m² – 2)x + m – 1 với m là tham số. Tìm m để:

Đề bài. a) Cho đoạn thẳng BC = 4cm. Vẽ tam giác đều ABC. Có thể vẽ được bao nhiêu tam giác như vậy?

Đề bài. Cho tanα = 2. Tính $\tan (α - \frac{π}{4})$ .

Đề bài. Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài BC. Tính góc B và góc C.

Đề bài. Tìm GTLN, GTNN của hàm số y = 3 – 4sin²xcos²x.

Đề bài. Cho hình chữ nhật ABCD có cạnh AD = a, M là trung điểm của cạnh AB. Biết rằng sin $\hat{M D B} = \frac{1}{3}$ . Tính độ dài của đoạn thẳng AB theo a.

Đề bài. Cho cos a = 0,2 với π < a < 2π. Tính $\cos \frac{a}{2}$ .

Đề bài. Thay dấu * bằng chữ số thích hợp để mỗi số sau là số nguyên tố:

Đề bài. Trong đêm định mệnh tại Uchiha Clan, Itachi ngồi lên cột đèn tại Lăng Lũ để nhìn đứa em trai bé bỏng Sasuke lần cuối. Biết Sasuke ngồi cách cột điện 20m và nhìn thấy đỉnh của cột điện đó với góc nâng 55°. Cho biết khoảng cách từ mắt của Sasuke tới mặt đất là 2m. Tìm chiều cao của cột điện.

Đề bài. Giải phương trình: $\sin (3 x + \frac{2 π}{3}) + \sin (x - \frac{7 π}{5}) = 0$ .

Đề bài. Cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành các tam giác đều ABM, AND. Gọi E, F, Q theo thứ tự là trung điểm của BD, AN, AM. Hỏi tam giác MNC là tam giác gì? Vì sao?

Đề bài. Cho phương trình: x² – (2m + 1)x + m² + 2 = 0. Tìm m để phương trình có 2 nghiệm x₁, x₂ thỏa mãn 3x₁x₂ – 5(x₁ + x₂) + 7 = 0.

Đề bài. Tìm x biết 20 – 2(x – 1)² = 2.

Đề bài. Chứng minh 2²⁰²⁰ + 2²⁰²¹ + 2²⁰²² + 7²⁰²³ + 7²⁰²⁴ chia hết cho 7.

Đề bài. Cho một cấp số nhân có công bội bằng 3 và số hạng đầu bằng 5. Biết số hạng chính giữa là 32805. Hỏi cấp số nhân đã cho có bao nhiêu số hạng?

Đề bài. Tìm các chữ số a, b để:

Đề bài. Ba người cùng làm một công việc. Nếu làm riêng, người thứ nhất mất 5 giờ, người thứ hai mất 4 giờ và người thứ ba mất 6 giờ mới làm xong công việc đó. Hỏi nếu ba người cùng làm thì sau 1 giờ làm được bao nhiêu phần công việc.

Đề bài. Xem hình vẽ, cho biết a// b và c ⊥ a.

Đề bài. Cho hình thoi EGHK với O là giao điểm của 2 đường chéo. Biết EG = 15 cm. Tính độ dài của GH, HK, KE?

Đề bài. Viết số có hai chữ số mà chữ số hàng chục bé hơn chữ số hàng đơn vị là 4.

Đề bài. Cho các số thực không âm a, b, c thay đổi thỏa mãn a² + b² + c² = 1. Tìm GTLN của biểu thức Q = $\sqrt{a + b} + \sqrt{b + c} + \sqrt{c + a}$ .

Đề bài. Cho các số thực x, y thỏa mãn: 4x² + 2xy + y² = 3.

Đề bài. Chứng minh rằng n² – n chia hết cho 2 với mọi n ∈ ℤ.

Đề bài. An có 90 bút bi và 150 quyển vở muốn chia thành các phần thưởng để ủng hộ học sinh nghèo, sao cho số bút và vở trong các phần thưởng là như nhau. Hỏi An chia được bao nhiêu số phần thưởng trong khoảng từ 5 đến 30 phần thưởng?

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

166

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.