Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 88)

Đề bài. Tam giác ABC nội tiếp (O), AD là đường kính của (O). M là trung điểm của của BC, H là trực tâm của tam giác ABC. Gọi X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC. Chứng minh rằng 4 điểm X, Y, Z, M cùng thuộc 1 đường tròn.

Lời giải:

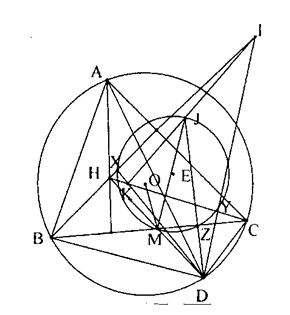
Giả sử HB cắt DY tại I, HC cắt DX tại K, J là trung điểm IK

Xét tam giác ADC có $\widehat{ACD}=90°$ (góc nội tiếp chắn nửa đường tròn)

Nên AC ⊥ CD

Mà BH ⊥ AC. Nên BH // CD

Tương tự: $\widehat{ABD}=90°$ (góc nội tiếp chắn nửa đường tròn)

Nên AB ⊥ BD

Mà CH ⊥ AB nên CH // BD

Xét tứ giác BHCD có: BH // CD và CH // BD nên BHCD là hình bình hành.

⇒ HD, BC cắt nhau tại trung điểm M của mỗi đường

Vì DX ⊥ HI, DI ⊥ HC suy ra K là trực tâm của tam giác IHD

Nên: $\widehat{KDI}=\widehat{KHI}=\widehat{HCD}$ (HI //CD)

$\widehat{CHD}=\widehat{KID}$(cùng phụ với )

Xét tam giác KID và tam giác CHD có:

$\widehat{KDI}=\widehat{HCD}$

$\widehat{KID}=\widehat{CHD}$

⇒ ∆KID ∽ ∆CHD (g.g)

Mặt khác CM, DJ là hai trung tuyến tương ứng của tam giác CHD và KID

Như vậy ta có: ∆DIJ ∽ ∆CHM

⇒ $\widehat{JDI}=\widehat{HCM}$

Từ đó suy ra: DJ vuông góc với BC tại Z hay Z thuộc đường tròn đường kính MJ.

Lại có: M là trung điểm HD (chứng minh trên)

X, Y, Z lần lượt là hình chiếu vuông góc của D lên HB, HC, BC

Kết hợp tính chất điểm M thì đường tròn đường kính MJ là đường trò Ơ–le của tam giác HID.

Suy ra: X, Y, Z, M cùng thuộc 1 đường tròn.