Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 102)

Câu 38: Tìm Min cuả biểu thức A = ( x- 1)( x + 2 )(x + 3)(x + 6) + 2045

Phương pháp giải: 

Nhóm các yếu tố trong biểu thức: Ta nhóm các yếu tố lại để dễ dàng tính toán. Nhận thấy rằng (x−1)(x+6) và (x+2)(x+3) là các cặp nhân có thể đơn giản hóa.

Nhân các biểu thức đã rút gọn.

Tìm giá trị nhỏ nhất và kết luận.

Lời giải:

A=(x−1)(x+2)(x+3)(x+6)+2045

$A=\left[(x-1)(x+6)\right]\left[(x+2)(x+3)\right]+2045$

$A=(x^2+5x-6)(x^2+5x+6)+2045$

$A={(x^2+5x)}^2-36+2045$

$A={(x^2+5x)}^2+2009$

Vì ${(x^2+5x)}^2\ge 0\Rightarrow {(x^2+5x)}^2+2009\ge 2009$

$\Rightarrow A\ge 2009$

=> GTNN của A bằng 2009 

Dấu '=' xảy ra khi ${(x^2+5x)}^2=0\iff x^2+5x=0\iff x(x+5)=0$

=> x = 0 hoặc x + 5 = 0 <=>  x = -5

Vậy GTNN của A bằng 2009.

Phương pháp chung

+ Với mọi x: 

+ Với mọi a; b ta có: 

. Dấu = xảy ra khi a+ b = 0 Và 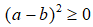 . Dấu = xảy ra khi a- b = 0

• Cho biểu thức A(x):

+ Nếu 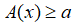 thì giá trị nhỏ nhất của biểu thức A(x) là a.

+ Nếu 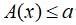 thì giá trị lớn nhất của biểu thức A(x) là a.

+ Nếu 

+ Nếu 

+ Với mọi A; B ta có: