a) Chứng minh rằng tích BM.DN có giá trị không đổi.

b) Gọi K là giao điểm của BN và DM. Tính  góc BKD

Phương pháp giải: 

a) Sử dụng các tính chất của hình thoi và tam giác đồng dạng để chứng minh tích $BM \cdot DN$ không đổi.

Tìm mối liên hệ giữa các đoạn thẳng và các góc trong tam giác để chứng minh $\triangle MBC$ đồng dạng với $\triangle CDN$.

Từ sự đồng dạng, suy ra tỉ số các cạnh tương ứng và chứng minh tích $BM \cdot DN$ không đổi.

b) Sử dụng tính chất của tam giác đều và tam giác đồng dạng để tính góc $\angle BKD$.

Chứng minh tam giác $\triangle ABD$ là tam giác đều.

Sử dụng tính chất tam giác đồng dạng và các góc trong tam giác để xác định góc $\angle BKD$.

Lời giải:

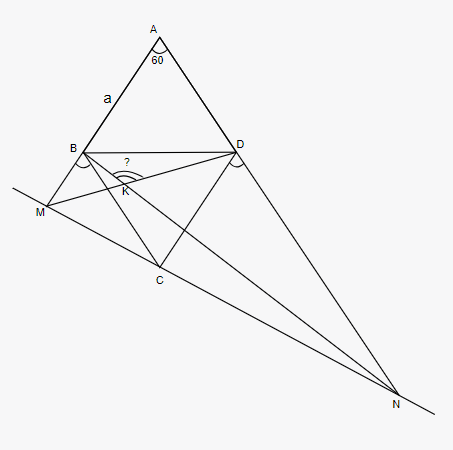
a) Ta có : $\widehat{ABC}=120^o\Rightarrow \widehat{MBC}=180^o-120^o=60^o$

Tương tự $\widehat{CDN}=60^o$=> $\widehat{MBC}=\widehat{CDN}$(1)

Mặt khác: $\widehat{BMC}=\widehat{BCD}=60^o$, Hai góc này ở vị trí so le trong 

=> BM//CD

=>  $\widehat{BMC}=\widehat{DCN}$( đồng vị ) (2)

Từ (1) , (2) 

=> ΔMBC đồng dạng với ΔCDN (g-g)

=> $\frac{BM}{DC}=\frac{BC}{DN}\Rightarrow BM\mathrm{.}DN=BC\mathrm{.}DC=a^2$ Không đổi

b) Xét tam giác ABD có: AB=AD =a => ABD cân và góc A bằng 60 độ

=> Tam giác ABD đều

=> AB=BD=AD=a

và $\widehat{MBD}=180^o-\widehat{ABD}=180^o-60^o=120^o$

Tương tự $\widehat{BDN}=120^o$

=> $\widehat{MBD}=\widehat{BDN}$(3)

Ta lại có: $MB\mathrm{.}DN=a^2=BD\mathrm{.}BD\Rightarrow \frac{MB}{BD}=\frac{BD}{DN}$​(4)

Từ (3), (4)  Suy ra ΔBMD=ΔDBN(c.g.c)

=> $\widehat{BMD}=\widehat{DBN}$

=> $\widehat{BKD}=\widehat{KBM}+\widehat{BMK}=\widehat{NBM}+\widehat{BMD}=\widehat{NBM}+\widehat{DBN}=\widehat{DBM}=120^o$.