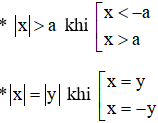Tìm số nguyên tố x để |P| + P = 0 biết P = (căn x

Tìm số nguyên tố x để |P| + P = 0 biết P = (căn x - 3)/(căn x + 3)

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Tiếng Anh. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 97)

Câu 5: Tìm số nguyên tố x để |P| + P = 0 biết $P = \frac{{\sqrt x - 3}}{{\sqrt x + 3}}(x \ge 0,x \ne 4,x \ne 9)$

Phương pháp giải:

* |x| ≥ 0 với mọi x ∈ Q. Dấu “=” xảy ra khi x = 0

* |x| ≥ x và |x| ≥ -x với mọi x ∈ Q

* |x| ≥ |x| với mọi x ∈ Q

Với a > 0, ta có:

* |x| = a khi x = ±a

* |x| ≤ a khi -a ≤ x ≤ a

Công thức tính giá trị tuyệt đối của một số hữu tỉ hay nhất

Lời giải:

Để |P| + P = 0 => P ≤ 0 =>

\[\begin{array}{l}\left. {\begin{array}{*{20}{c}}{\frac{{\sqrt x - 3}}{{\sqrt x + 3}} \le 0}\\{m\`a \sqrt x + 3 > 0}\end{array}} \right\} = > \sqrt x - 3 \le 0\\ = > \sqrt x \le 3 = > 0 \le x \le 9\end{array}\]

Kết hợp với ĐKĐB: $\left\{ {\begin{array}{*{20}{c}}{0 \le x < 9}\\{x \ne 4}\end{array}} \right.$

Mà x là số nguyên tố => x = {2, 3, 5, 7}

Xem thêm các câu hỏi thường gặp môn Toán hay nhất:

Câu 1: 40 : 3 bằng bao nhiêu...

Câu 2: Viết tiếp 2 số hạng vào dãy số sau...

Câu 3: Cho hệ phương trình $\left\{ {\begin{array}{*{20}{c}}{(m - 1)x - 2y = 1}\\{3x + my = 1}\end{array}} \right.$...

Câu 4: Tìm x, y biết x(x - y) = $\frac{3}{{10}}$ và y(x - y) = $ - \frac{3}{{50}}$...

Câu 5: Tìm số nguyên tố x để |P| + P = 0 biết $P = \frac{{\sqrt x - 3}}{{\sqrt x + 3}}(x \ge 0,x \ne 4,x \ne 9)$...

Câu 6: Tìm số tự nhiên x, y biết 7(x - 2004)² = 23 - y ²...

Câu 7: Bạn Lan đánh số trang sách bằng các số tự nhiên từ 1 đến 216. Bạn Lan phải viết tất cả bao nhiêu chữ số?...

Câu 8: Tìm số liền trước số 9...

Câu 9: Cho hai tia Ox và Oy đối nhau. Vẽ tia Oz sao cho góc xOz = $\frac{4}{9}$ góc xOy ....