Cho ΔABC có BC = 6, AB = 5, và BC.BA = 24. Tính độ dài trung tuyến BM và cosin của góc nhọn tạo bởi BM và đường cao AH

Cho ΔABC có BC = 6, AB = 5, và BC.BA = 24. Tính độ dài trung tuyến BM và cosin của góc nhọn tạo bởi BM và đường cao AH

Nguyễn Mạnh Tài Ngày: 04-04-2024 Tổng hợp kiến thức

38

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 93)

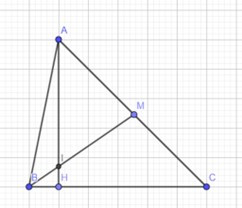
Đề bài. Cho ΔABC có BC = 6, AB = 5, và $\vec{B C} . \vec{B A} = 24$ . Tính độ dài trung tuyến BM và cosin của góc nhọn tạo bởi BM và đường cao AH.

Lời giải:

15000 câu hỏi ôn tập môn Toán có đáp án (Phần 103) (ảnh 1)

Áp dụng định lý cosin ta có:

$A C = \sqrt{B A^{2} + B C^{2} - 2. B A . B C . \cos B} = \sqrt{B A^{2} + B C^{2} - 2. (\vec{B C} . \vec{B A} = 24)} = \sqrt{5^{2} + 6^{2} - 2.24} = \sqrt{13}$

Xét tam giác ABC có BM là trung tuyến

Suy ra: $B M = \sqrt{\frac{2 (A B^{2} + B C^{2}) - A C^{2}}{4}} = \sqrt{\frac{109}{4}} = \frac{\sqrt{109}}{2}$

Do $\vec{B C} . \vec{B A} = 24 > 0$ nên $\hat{B} < 90 °$ nên ta có hình vẽ như trên

Gọi I là giao điểm của AH và BM

$\cos \hat{M B C} = \frac{B M^{2} + B C^{2} - M C^{2}}{2. B M . B C} = 0, 958$

Suy ra: $\cos \hat{I B H} = 0, 958$

Xét tam giác IBH có: $\cos \hat{I B H} = 0, 958; \hat{I H B} = 90 °$

Suy ra: $\sin \hat{B I H} = \cos \hat{I B H} = 0, 958 \Rightarrow \cos \hat{B I H} = \sqrt{1 - 0, 958^{2}} = 0, 287$

Suy ra: $\cos (B M, A H) = 0, 287$ .

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của SC.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi K, J lần lượt là trọng tâm tam giác ABC và tam giác SBC. Xác định thiết diện hình chóp cắt bởi mặt phẳng chứa KI và song song AD.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và $\hat{B A D} = 120 °$ , SA = SB = SC, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60 độ.Tính thể tích V của khối chóp S.ABCD.

Đề bài. Cho hình chóp S.ABCD có đáy là hình thang (AB//CD và AB = 3CD). Gọi H là điểm thuộc cạnh SC sao cho SH = 3HC. Gọi K là giao điểm của SB và (ADH). Tính tỉ số $\frac{S K}{S B}$ .

Đề bài. Cho khối chóp S.ABC có đáy ABC là tam giác vuông tại C, BC= a, $\hat{B S C} = 60 °$ cạnh SA vuông góc với đáy, mặt phẳng (SBC) tạo với (SAB) góc 30 độ. Thể tích khối chóp đã cho.

Đề bài. Cho hình chóp S. ABC. Gọi M, N lần lượt là trung điểm của AC, BC, H, K lần lượt là trọng tâm của tam giác SAC, SBC.

Đề bài. Cho hình chóp S.ABCD với ABCD có các cạnh đối diện không song song với nhau và M là một điểm trên SA. Tìm giao điểm của đường thẳng và MC và (SBD).

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, biết AB = a; $A D = a \sqrt{3}$ . Hình chiếu S lên đáy là trung điểm H cạnh AB, góc tạo bởi SD và đáy là 60°. Tính thể tích V khối chóp S.ABCD.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA = a, $S B = a \sqrt{3}$ . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD). Tính khoảng cách từ điểm C đến mặt phẳng (SAD).

Đề bài. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của cạnh SD, N thuộc cạnh SA sao cho NS = 2NA. Gọi I là giao điểm của mp (OMN) và cạnh CD. Tính $\frac{I C}{I D}$ .

Đề bài. Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của cạnh SC.

Đề bài. Cho hình chóp S.ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD; F là giao điểm của IK và SE; M là giao điểm của JK và BD. Tìm giao điểm của (IJK) và SD.

Đề bài. Cho hình chóp SABCD có đáy là hình thang với AD là đáy lớn, P thuộc SD. Gọi M, N là lần lượt trung điểm của AB, BC. Tìm thiết diện của hình chóp cắt bởi mặt phẳng MNP tứ diện này là hình gì?

Đề bài. Cho chóp S.ABCD đáy là hình thang đáy lớn AD. Gọi I là trung điểm SA, J ∈ AD sao cho $J D = \frac{1}{4} A D$ ; K ∈ SB : SK = 2BK. Tìm giao tuyến:

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Chứng minh đường thẳng OI song song với mặt phẳng (SAB) và mặt phẳng (SAD).

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN / BS, NP // CD, MQ // CD. Hỏi PQ song song với mặt phẳng nào?

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA và SB. Chứng minh rằng đường thẳng NC song song với đường thẳng MD.

Đề bài. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của các đoạn BC, CD, SO. Tìm giao tuyến của (MNP) với các mặt phẳng (SAB), (SAD), (SBC) và (SCD).

Đề bài. Cho hình chữ nhật ABCD có cạnh AD = a, M là trung điểm của cạnh AB. Biết rằng $s i n \hat{M D B} = \frac{1}{3}$ . Tính độ dài của đoạn thẳng AB theo a.

Đề bài. Cho hình chữ nhật ABCD, kẻ BH vuông góc với AC. Trên AC, CD ta lấy các điểm M, N sao cho $\frac{A M}{A H} = \frac{D N}{D C}$ . Chứng minh bốn điểm M, B, C, N nằm trên một đường tròn.

Đề bài. Cho hình chữ nhật ABCD. Điểm E nằm ngoài hình chữ nhật sao cho $\hat{A E C} = 90 ° .$ Chứng minh rằng $\hat{B E D} = 90 ° .$

Đề bài. Cho hình chữ nhật ABCD. H là hình chiếu của B trên AC. M; K theo thứ tự là trung điểm của AH và CD. I và O lần lượt là trung điểm của AB và IC. Chứng minh:

Đề bài. Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, BC = 2, AA' = 2. Khoảng cách giữa hai đường thẳng AD' và DC' bằng? (tham khảo hình)

Đề bài. Cho hình hộp đứng ABCD.A'B'C'D', AB = AD = a, . Gọi M, N lần lượt là trung điểm của các cạnh A'D' và A'B'. Tính thể tích khối chóp A.BDMN.

Đề bài. Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45°. Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?

Đề bài. Cho hình lăng trụ đứng tam giác ABC.A'B'C' có cạnh A B' = 3 cm, BC = 5 cm, AC' = 6 cm, AA' = 7 cm. Độ dài cạnh BC bằng

Đề bài. Cho hình thang ABCD (AB // CD) có $\hat{D} = 50 °; \hat{C} = 36 °$ , AB = 4cm, AD = 6cm.

Đề bài. Hình thang ABCD (AB // CD) có AD = 15 cm; AC = 12 cm và CD = 13cm. Biết diện tích hình thang là 45 cm². Tính chiều cao hình thang.

Đề bài. Hình thang ABCD (AB // CD) có $\hat{A} - \hat{D} = 20 °; \hat{B} = 2 \hat{C}$ . Tính các góc của hình thang.

Đề bài. Cho hình thang ABCD như hình bên. Tìm a biết diện tích hình thang là 150cm².

Đề bài. Cho hình thang vuông có đáy AB = a, CD = 2a đường cao AD = a. Xác định $|\vec{D A} - \vec{A B} - \vec{C D}|$ .

Đề bài. Cho hình thang cân ABCD có CD = 2AB = 12cm, chu vi tam giác ACD là 25cm. Chu vi tam giác ABC là ...cm.

Đề bài. Cho hình thang cân ABCD với cạnh đáy là AB và CD. Biết BD = 6cm, BC = 4cm. Tính AC, AD.

Đề bài. Cho hình thang cân ABCD (AB // CD, AB < CD), BC = 15cm, đường cao BH = 12cm, DH = 16cm. Chứng minh BD vuông góc với BC.

Đề bài. Cho hình thang MNPQ (MN // PQ), có MP = NQ. Qua N kẻ đường thắng song song với MP, cắt đường thẳng PQ tại K. Chứng minh:

Đề bài. Cho hình thang vuông ABCD ( $\hat{A} = \hat{D} = 90 °$ ) cạnh $A B = \frac{1}{2} C D$ , gọi H là hình chiếu của D lên AC. M, N là trung điểm của HC và HD.

Đề bài. Cho hình thoi ABCD có BC = 5cm. Chu vi hình thoi ABCD là:

Đề bài. Cho hình thoi ABCD có cạnh bằng a, $\hat{B A D} = 60 °$ . Tính $|\vec{A B} + \vec{A D}|$ .

Đề bài. Cho hình thoi ABCD có cạnh bằng a, O là tâm hình thoi, $\hat{B A D} = 120 °$ . Tính $|\vec{A D} - \vec{O C}|$ .

Đề bài. Cho hình thoi ABCD có cạnh bằng a, $\hat{B A D} = 30 °$ . Tính diện tích hình thoi ABCD.

Đề bài. Cho hình thoi ABCD, O là giao điểm hai đường chéo. Vẽ đường thẳng qua B song song AC, vẽ đường thẳng qua C song song với BD, hai đường thẳng đó cắt nhau tại K.

Đề bài. Cho hình thoi ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh MNPQ là hình chữ nhật.

Đề bài. Cho tứ diện ABCD và điểm M thuộc AB và N thuộc CD; điểm G nằm trong tam giác BCD. Tìm giao tuyến của (GMN) và (ACD).

Đề bài. Cho hình vẽ sau:

Đề bài. Cho hình vẽ:

Đề bài. Cho hình vẽ. Biết AB // CD, CD // EG. $\hat{A} = 40 °; \hat{E} = 50 °$ . Tính $\hat{A C D}, \hat{A C E}$ .

Đề bài. Cho tam giác ABC. Gọi M là trung điểm BC và I là trung điểm AM. Chứng minh rằng $2 \vec{I A} + \vec{I B} + \vec{I C} = \vec{0}$ .

Đề bài. Cho hình vuông ABCD có AB = 4, gọi E là trung điểm của cạnh CD và F là điểm thuộc cạnh AC sao cho CF= 3AF. Tính độ dài cạnh EF.

Đề bài. Cho hình vuông ABCD cạnh a có O là giao điểm của 2 đường chéo. Tính $|\vec{O A} - \vec{C B}|$ .

Đề bài. Cho hình vuông ABCD có cạnh là a. Trên cạnh BC lấy điểm E, đường thẳng AE cắt đường thẳng CD tại điểm M. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh $\frac{1}{A E^{2}} + \frac{1}{A M^{2}} = \frac{1}{a^{2}}$ .

Đề bài. Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND tính $\hat{B M N}$ .

Đề bài. Cho hình vuông ABCD và CDIS không thuộc mặt phẳng và cạnh bằng 4. biết tam giác SAC cân tại S, SB = 8. Thiết diện của mp ACI và hình chóp ABCD có diện tích bao nhiêu?

Đề bài. Cho hình vuông ABCD, M là điểm nằm trên đoạn thẳng AC sao cho $A M = \frac{A C}{4}$ ; N là trung điểm của đoạn thẳng DC. Chứng minh tam giác BMN vuông cân.

Đề bài. Cho hàm số y = (m – 3)x.

Đề bài. Cho khối chóp S.ABCD có đáy ABCD là hình bình hành, SA = SB = SC = AC = a, SB tạo với mặt phẳng (SAC) một góc 30°. Tính thể tích khối chóp.

Đề bài. Cho log₆15 = a; log₁₂18 = b. Biểu diễn log₂₅24 theo a và b.

Đề bài. Cho lục giác đều ABCDEF tâm O, xác định các vectơ

. $\vec{A B} + \vec{O D}; \vec{A B} + \vec{A E} + \vec{O D}$

Đề bài. Cho P là 1 điểm bên trong hình chữ nhật ABCD sao cho PA = 3cm, PD = 4cm, PC = 5cm. Hãy tính độ dài đoạn thẳng PB?

Đề bài. Một phép chia có thương là 7 và số dư là 112. Biết tổng của số bị chia, số chia, thương và số dư là 1375. Tìm phép chia đó.

Đề bài. Cho phương trình cos5x = 3m - 5. Đoạn [a; b] là tập hợp tất cả các giá trị của m để phương trình có nghiệm. Tính 3a + b.

Đề bài. Tìm số nghiệm nguyên không âm, số nghiệm dương của phương trình x + y + z = 100.

Đề bài. Cho phương trình x² + 4x + 4a – a² = 0. Tìm a để phương trình có hai nghiệm phân biệt x₁; x₂ thỏa mãn x₁ = x₂² – 6.

Đề bài. Cho phương trình: x² – 3x + 3m – 1 = 0. Tìm m để phương trình có nghiệm.

Đề bài. Cho phương trình (3x + 2k – 5)(x – 3k + 1) = 0, trong đó k là một số. Tìm các giá trị của k sao cho một trong các nghiệm của phương trình là x = 1.

Đề bài. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, SD và OC. Gọi giao điểm của (MNP) với SA là K. Tính tỉ số $\frac{K S}{K A}$ .

Đề bài. Cho sin α = $\frac{3}{5}$ và 90° < α < 180°. Tính giá trị của biểu thức $C = \frac{\cot α - 2 \tan α}{\tan α + 3 \cot α}$ .

Đề bài. Cho $\sin x = \frac{4}{5}; x \in (- \frac{π}{2}; 0)$ . Tính giá trị của sin2x.

Đề bài. Cho $\sin a = \frac{8}{17}; \tan b = \frac{5}{12}$ và a, b là các góc nhọn. Tính A = sin(a – b).

Đề bài. Cho số thực x lớn hơn 1 và ba số thực dương a, b, c khác 1 thỏa mãn điều kiện log_ax > log_bx > log_cx. So sánh a, b, c?

Đề bài. Cho tam giác ABC vuông tại A có $\hat{B} = 50 °$ . Tính tỉ số lượng giác góc $\hat{C}$ .

Đề bài. Cho tam giác ABC vuông tại A, các trung tuyến AD và BE vuông góc với nhau tại G. Biết $A B = \sqrt{6}$ cm, tính BC.

Đề bài. Cho tam giác ABC biết AB = 50, BC = 70, $\hat{A} = 30 °$ . Tính gần đúng diện tích tam giác ABC.

Đề bài. Cho tam giác ABC cân tại A; góc A = 120 độ và AB = AC = a. Tính $\vec{B A} . \vec{C A}$ .

Đề bài. Cho tam giác ABC cân tại A đường trung trực của AB cắt BC tại K. Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp tam giác ACK.

Đề bài. Cho tam giác ABC cân tại A nội tiếp đường tròn (O), AC = 5a, BC = 6a. Tính khoảng cách từ điểm O đến dây BC theo a.

Đề bài. Cho tam giác ABC cân tại A sao cho $\hat{B A C} = 40 °$ và $\hat{A C B} = 70 °$ . Ở phía ngoài tam giác ABC, dựng tam giác cân ADC sao cho $\hat{C A D} = \hat{A C D} = 35 °$ . Tính $\hat{B D C}$ .

Đề bài. Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Các đường thẳng vuông góc với BC kẻ từ D và E cắt AB, AC lần lượt ở M, N.

Đề bài. Cho tam giác ABC cân tại A. Từ một điểm D trên đáy BC, ta vẽ đường thẳng vuông góc với BC, cắt các cạnh AB, AC lần lượt tại E, F. Vẽ các hình chữ nhật BDEH, CDFK. Chứng minh rằng A là trung tâm điểm của HK.

Đề bài. Cho tam giác ABC, điểm M thuộc cạnh AB sao cho 3AM = AB và N là trung điểm của AC. Tính $\vec{M N}$ theo $\vec{A B}, \vec{A C}$ .

Đề bài. Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Dựng đường tròn (K) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm F, E. Gọi H là giao điểm của BE và CF.

Đề bài. Cho tam giác ABC có: $2 \hat{B} + 3 \hat{C} = 180 °$ . Chứng minh BC² = BC.AC + AB².

Đề bài. Cho tam giác ABC có $\hat{A} = 60 °; \hat{B} = 40 °$ ; AB = 10cm.

Đề bài. Cho tam giác ABC, AB = AC = a, góc A = 120°, lấy điểm M trên cạnh BC sao cho 5BM = 2BC. Tính độ dài đoạn AM?

Đề bài. Cho tam giác ABC có A(1;3), B(-1;-5), C(-4;-1). Viết phương trình đường cao AH của tam giác ABC.

Đề bài. Cho tam giác ABC có độ dài 3 cạnh: AB = 20 cm, AC = 34cm, BC = 42 cm. Diện tích của tam giác đó là bao nhiêu?

Đề bài. Cho tam giác ABC có AB = 3, BC = 5, AC = 6. Trên cạnh AB lấy điểm M sao cho BM = 2AM, trên cạnh BC lấy điểm K sao cho 3KB = 2KC. Tính MK.

Đề bài. cho tam giác ABC có AB = 12cm, AC=15cm. Trên cạn AB lấy M sao cho AM = 8cm, trên AC lấy N sao cho AN = 10cm. lấy D là điểm bất kì trên BC. AD cắt MN tại E. Tính tỉ số $\frac{A E}{A D}$ .

Đề bài. Cho ∆ABC có AB = 2, AC = 3, $\hat{A} = 60 °$ . Tính độ dài phân giác $\hat{A}$ .

Đề bài. Cho tam giác ABC có $\hat{B} = 70 °; \hat{C} = 30 °$ . Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC). Tính $\hat{A D H}$ .

Đề bài. Cho ΔABC có BC = 6, AB = 5, và $\vec{B C} . \vec{B A} = 24$ . Tính độ dài trung tuyến BM và cosin của góc nhọn tạo bởi BM và đường cao AH.

Đề bài. Cho ΔABC cố định, các điểm D và E di động trên các cạnh tương ứng là AB và AC sao cho $\frac{A D}{B D} = \frac{C E}{E A}$ . Chứng minh rằng: Trung điểm M của đoạn thẳng DE nằm trên 1 đoạn thẳng cố định.

Đề bài. Cho tam giác ABC có đường phân giác trong AD = 6, nó chia cạnh BC thành hai đoạn BD = 2, CD = 3. Tính AB, AC.

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Tìm tập xác định tan(x-pi/4)

Tìm tập xác định tan(x-pi/4) Nguyễn Mạnh Tài

35

Toán Tổng hợp kiến thức

Để lát nền một căn phòng hình chữ nhật có chiều dài 27m, chiều rộng 15m, Người ta cần dùng một số viên gạch hình vuông có cạnh 30cm

Để lát nền một căn phòng hình chữ nhật có chiều dài 27m, chiều rộng 15m, Người ta cần dùng một số viên gạch hình vuông có cạnh 30cm Nguyễn Mạnh Tài

29

Toán Tổng hợp kiến thức

Một phòng học hình chữ nhật có chiều dài 15m và chiều rộng 7m. Người ta mua loại gạch hình vuông có cạnh 0,5m để lát nền toàn bộ phòng học

Một phòng học hình chữ nhật có chiều dài 15m và chiều rộng 7m. Người ta mua loại gạch hình vuông có cạnh 0,5m để lát nền toàn bộ phòng học Nguyễn Mạnh Tài

23

Toán Tổng hợp kiến thức

Một lớp học có 20 học sinh nam và 24 học sinh nữ. Có thể chia lớp đó thành nhiều nhất bao nhiêu tổ để số nam và số nữ được chia đều vào các tổ

Một lớp học có 20 học sinh nam và 24 học sinh nữ. Có thể chia lớp đó thành nhiều nhất bao nhiêu tổ để số nam và số nữ được chia đều vào các tổ Nguyễn Mạnh Tài

29

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack57. All Rights Reserved.