Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 19)
Câu 49: Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A , (O2) tại B . O2H cắt (O1) tại C và (O1) tại D. Chứng minh rằng ba đường thẳng BC, BD, HK đồng quy tại 1 điểm.
Lời giải:
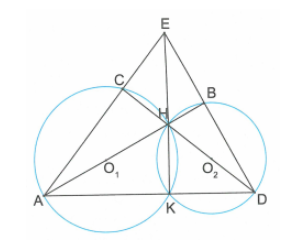
Gọi giao điểm của AC và BD là E
Các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C, tam giác AHK vuông tại K
Suy ra
Các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K, tam giác HBD vuông tại B
Suy ra
Từ (2) và (3) suy ra A, K, D thẳng hàng
Do đó HK ⊥ AD
Từ (1) và (4) suy ra H là trực tâm tam giác AED
Do đó HE ⊥ AD
Suy ra H thuộc EK
Vậy BC, BD, HK đồng quy tại 1 điểm.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng...
Câu 3: Cho bảng biến thiên hàm số y = f(x) như sau:..
Câu 4: Cho hàm số y = f(x) = – 3x....
Câu 5: Tìm m để hàm số y = có tập xác định là ℝ....
Câu 7: Tìm đa thức M biết (x3 – 5x2 + x – 5) = (x – 5).M...
Câu 8: Cho a, b, c > 0. Chứng minh ...
Câu 9: Cho tam giác ABC có a = 8, b = 10, . Độ dài cạnh c là...
Câu 10: Cho các điểm A(1; – 2), B(– 2; 3) và C(0; 4). Diện tích tam giác ABC bằng bao nhiêu?...
Câu 11: Cho tập hợp A = (– ∞; 2023), B = [4 – 3m; + ∞). Tìm m để CRB ⊂ A....
Câu 13: Cho số phức z thỏa mãn + z = 3 + 4i. Mô đun của z bằng?...
Câu 14: Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; – 7) và B (2; – 8). Tính y(– 1)....
Câu 16: Tìm điểm thuộc đồ thị y = – x + 2 có hoành độ gấp 3 lần tung độ.....
Câu 17: Cho a và b là hai số dương khác nhau thỏa mãn .....
Câu 18: Cho A (– 1; 2); B(2; 0); C(3; 4)....
Câu 19: Cho tam giác đều cạnh a, trọng tâm G . Tính ......
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
