Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 108)

Câu 14: 

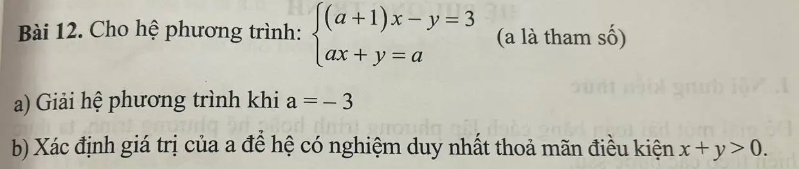
Phương pháp giải: 

a) Đặt a = - 3 vào hệ phương trình, ta được hệ phương trình mới. Giải hệ phương trình này ta được nghiệm (x, y) = (1, -1).

b) Để hệ phương trình có nghiệm duy nhất, ta cần đảm bảo rằng hệ số của x và y trong hai phương trình không tỷ lệ với nhau. Từ đó, ta có:

$\frac{a+1}{a}\ne \frac{-1}{1}$

Giải phương trình trên ta được a ≠ -1.

Để thoả mãn điều kiện x + y > 0, ta cần giải hệ phương trình và tìm giá trị của a sao cho x+y>0.

Lời giải:

a) Khi a = -3, hệ phương trình trở thành:

$\left\{\begin{array}{l}-2x-y=3\\ -3x+y=-3\end{array}\right.$

Giải hệ phương trình trên ta được nghiệm (x, y) = (1, -1).

b)

Điều kiện để hệ có nghiệm duy nhất:

Hệ phương trình: $\begin{cases} (a+1)x - y = a, \\ ax + y = a. \end{cases}$​

Hệ có nghiệm duy nhất khi định thức khác 0:
$\Delta = \begin{vmatrix} a+1 & -1 \\ a & 1 \end{vmatrix} = (a+1)(1) - (-1)(a) = a+1 + a = 2a+1.$

Điều kiện: $\Delta \neq 0$, tức $2a + 1 \neq 0$.

Giải: $a \neq -\frac{1}{2}$

Giải hệ phương trình:

Sử dụng phương pháp thế hoặc cộng đại số: $x = \frac{a + a^2}{2a + 1}, \quad y = \frac{a}{2a + 1}.$

Điều kiện $x + y > 0$:

Tổng: $x + y = \frac{a + a^2}{2a+1} + \frac{a}{2a+1} = \frac{a^2 + 2a}{2a+1}.$

Điều kiện $x + y > 0$: $\frac{a^2 + 2a}{2a+1} > 0.$

Tử số: $a^2 + 2a = a(a+2).$

Mẫu số: $2a+1.$

$\frac{a(a+2)}{2a+1} > 0$ khi biểu thức cùng dấu ở tử và mẫu.

Nghiệm: $a \in (-2, -\frac{1}{2}) \cup (0, \infty).$

Giá trị $a$ thỏa mãn: $a \in (-2, -\frac{1}{2}) \cup (0, \infty).$