Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 94)

Đề bài. Cho tam giác ABC nhọn, các đường cao BD và CE. Tia phân giác của các góc ABD và ACE cắt nhau tại O, cắt AC và AB lần lượt tại N và M. Tia BN cắt CE tại K,tia CM cắt BD tại H. Chứng minh rằng:

a) BN vuông góc CM.

b) Tứ giác MNHK là hình thoi.

Lời giải:

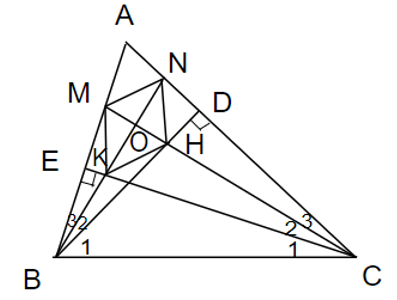a) Vì tam giác BEC vuông ở E

⇒ $\widehat{B_1}+\widehat{B_2}+\widehat{B_3}+\widehat{C_1}={90}^{\circ }$( phụ nhau)

Mà $\widehat{B_2}=\widehat{B_3}$ ( BN là phân giác góc ABD)

⇒ $\widehat{B_1}+2\widehat{B_2}+\widehat{C_1}={90}^{\circ }$

Vì tam giác DBC vuông ở D ⇒ $\widehat{C_1}+\widehat{C_2}+\widehat{C_3}+\widehat{B_1}={90}^{\circ }$(phụ nhau)

Mà $\widehat{C_2}={\widehat{B_1}}^{\circ }$CM là tia phân giác góc ACE)

⇒ $\widehat{C_1}+2\widehat{C_2}+\widehat{B_1}={90}^{\circ }\left(2\right)$

Lấy (1) + (2) ta được:

$\widehat{B_1}+2\widehat{B_2}+\widehat{C_1}+\widehat{C_1}+2\widehat{C_2}+\widehat{B_1}={90}^{\circ }Â\mathrm{ }+{90}^{\circ }Â\mathrm{ }={180}^{\circ }$

⇔ $2(\widehat{OBC}+\widehat{OCB})={180}^{\circ }$

⇔ $\widehat{OBC}+\widehat{OCB}={90}^{\circ }$

Xét tam giác OBC có: $\widehat{OBC}+\widehat{OCB}+\widehat{BOC}={180}^{\circ }$

⇒ $\widehat{BOC}={90}^{\circ }$

⇒ OB ⊥ OC

⇒ BN ⊥ CM

b) Vì BN ⊥ CM (cmt)

⇒ MH ⊥ KN

Xét tứ giác MNHK có 2 đường chéo MH và KN vuông góc với nhau

⇒ MNHK là hình thoi.