Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 91)

Đề bài. Cho góc $\widehat{xOy}$ . Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC.

b) DEAB = DECD.

c) OE là tia phân giác của góc xOy.

Lời giải:

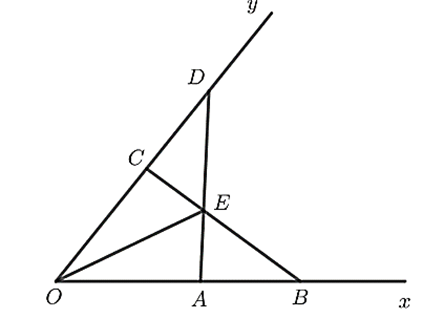
a) Xét tam giác OAD và tam giác OCB có:

OA = OC (giả thiết)

$\widehat{O}$chung

OD = OB

Do đó: ∆OAD = ∆OCB (c.g.c)

Suy ra: AD = BC

b) Do OA = PC, OB = OD nên OB – OA = OD – OC hay AB = CD

Do ∆OAD = ∆OCB (c.g.c) nên $\widehat{ODA}=\widehat{OBC}$

$\widehat{ECD}$ là góc ngoài tại định C của tam giác OBC nên $\widehat{ECD}=\widehat{COB}+\widehat{OBC}\left(1\right)$

$\widehat{EAB}$ là góc ngoài tại định C của tam giác OAD nên $\widehat{EAB}=\widehat{AOD}+\widehat{ODA}\left(2\right)$

Từ (1) và (2) suy ra: $\widehat{ECD}=\widehat{EAB}$

Xét tam giác EAB và ECD có:

$\widehat{ECD}=\widehat{EAB}$

AB = CD

$\widehat{EDC}=\widehat{EBA}$

Do đó: ∆EAB = ∆ECD (g.c.g)

c) Do ∆EAB = ∆ECD (g.c.g) nên BE = DE

Xét tam giác ODE và OBE có:

OD = OB

OE chung

BE = DE

Do đó: ∆ODE = ∆OBE (c.c.c)

Suy ra: $\widehat{EOD}=\widehat{EOB}$

Vậy OE là tia phân giác của $\widehat{xOy}$ .