Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 83)
Câu 44: Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ. Đồ thị hàm số y = f ‘(x) như hình vẽ sau:
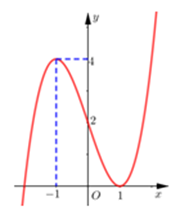
Số điểm cực trị của hàm số y = f (x) − 4x là:
Lời giải:
Đặt: g (x) = f (x) − 4x
Ta có: g’(x) = f ‘(x) − 4 = 0 ⇔ f ‘(x) = 4
Dựa vào đồ thị, suy ra phương trình f ‘(x) = 4 có 2 nghiệm x1; x2 trong đó x1 = −1 là nghiệm kép và x2 > 1 là nghiệm đơn.
Suy ra phương trình g’(x) = 0 có 2 nghiệm x1; x2 nhưng g’(x) đổi dấu duy nhất 1 lần khi qua nghiệm x2 này.
Vậy hàm số y = f (x) − 4x có một điểm cực trị.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
