Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C
Bài 3: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C, vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) Tứ giác ABCD nội tiếp.
b) CA là phân giác góc SCB.
Lời giải:
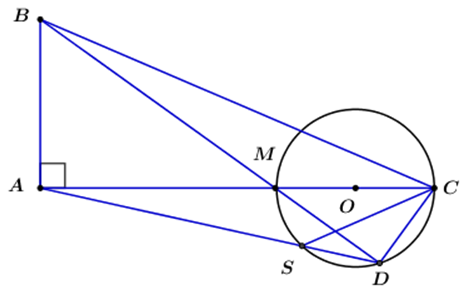
a) Tứ giác ABCD nội tiếp.
Do MC là đường kính của đường tròn (O), D thuộc (O) nên: ∠MDC = 900 = ∠BAC
Suy ra D và A cùng nhìn BC dưới một góc vuông
⇒ Tứ giác ABCD nội tiếp đường tròn đường kính BC.
b) CA là phân giác góc SCB.
Do ABCD là tứ giác nội tiếp nên: (cùng chắn cung AB).
Xét (O) ta có: (hai góc nội tiếp cùng chắn cung MS)
⇒ ∠ACB = ∠ ACS ( = ∠BDA).
Vậy CA là phân giác của ∠SCB (đpcm).
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Bài 2: Cho hàm số y = x - 2 có đồ thị là d.Tìm điểm trên d có hoành độ và tung độ đối nhau....
Bài 5: Tìm chữ số tận cùng của các số: .....
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm....
Bài 11: Có bao nhiêu số nguyên âm m để hàm số đồng biến trên khoảng ....
Bài 12: Tìm x ∈ BC(16; 21; 25) và x ≤ 400....
Bài 18: Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm....
Bài 23: Cho a,b,c là các số không âm thỏa mãn a + b + c = 1. Chứng minh ....
Bài 25: Tìm hệ số của x6 trong khai triển với biết n là số nguyên dương thỏa mãn điều kiện ....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
