Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a

Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a

Đỗ Thị Ngọc Ánh Ngày: 28-02-2023 Tổng hợp kiến thức

639

Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a

Bài 38: Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a và O là tâm của đáy. Gọi M, N, P và Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và là điểm đối xứng của S qua O. Tính thể tích của khối chóp S'.MNPQ

Lời giải:

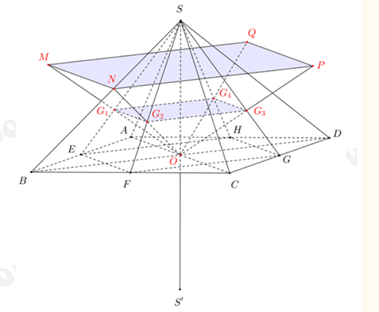
Tài liệu VietJack

Gọi $G_{1}, G_{2}, G_{3}, G_{4}$ lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.

Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

Ta có: $S_{M N P Q} = 4 S_{G_{1} G_{2} G_{3} G_{4}} = 4. \frac{4}{9} . S_{E F G H} = 4. \frac{4}{9} . \frac{1}{2} . E G . H F = \frac{8 a^{2}}{9} .$

Mặt khác:

$\begin{array}{l} d (S^{'}, (M N P Q)) = d (S^{'}, (A B C D)) + d (O, (M N P Q)) \\ = d (S, (A B C D)) + 2 d (O, (G_{1} G_{2} G_{3} G_{4})) \\ = d (S, (A B C D)) + \frac{2}{3} d (S, (A B C D)) \\ = \frac{5}{3} d (S, (A B C D)) = \frac{5 a \sqrt{14}}{6} . \end{array}$

Vậy thể tích của khối chóp S'.MNPQ là:

$V_{S^{'} . M N P Q} = \frac{1}{3} . \frac{5 a \sqrt{14}}{6} . \frac{8 a^{2}}{9} = \frac{20 a^{3} \sqrt{14}}{81} .$

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Bài 1: Cho điểm M có hoành độ là -2 và điểm M thuộc đồ thị hàm số y = −2x² . Xác định tọa độ điểm M...

Bài 2: Cho hàm số y = x - 2 có đồ thị là d.Tìm điểm trên d có hoành độ và tung độ đối nhau....

Bài 3: Cho tam giác ABC vuông tại A. Trên cạnh AC lấy M: 2MC < AC và M không trùng với C, vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:....

Bài 4: Cho đường tròn tâm O bán kỉnh và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB ?....

Bài 5: Tìm chữ số tận cùng của các số: .....

Bài 6: Cho hàm số y = 3x⁴+ 2(m − 2018)x²+ 2017 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có ba điểm cực trị tạo thành tam giác có một góc bằng 120°...

Bài 7: Cho hs: y = x⁴+ 2mx²+ m²+ m (1) ( m là tham số). Xác định m để hs (1) có 3 cực trị, đồng thời các điểm cực trị của đồ thị tạo thành 1 tam giác có góc bằng 120 độ.....

Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm....

Bài 9: Cho tam giác ABC có diện tích 60cm². Gọi M, N lần lượt là trung điểm của BC và AC. Tính diện tích tam giác AMN ?...

Bài 10: Cho hình bình hành ABCD có diện tích là S. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Tính diện tích tứ giác MNDC theo S....

Bài 11: Có bao nhiêu số nguyên âm m để hàm số $y = \frac{1}{3} {cos}^{3} x - 4cotx - (m + 1) cosx$ đồng biến trên khoảng $(0; π)$ ....

Bài 12: Tìm x ∈ BC(16; 21; 25) và x ≤ 400....

Bài 13: Cho tam giác ABC vuông ở B, trên cạnh AC lấy điểm E sao cho AE = AB. Tia phân giác của góc A cắt BC tại D....

Bài 14: Cho đường tròn tâm O, đường kính AB và một điểm C di động trên đoạn AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F...

Bài 15: Cho đường tròn (O) đường kính AB, vẽ góc ở tâm $\hat{A O C} = 55^{0}$ . Vẽ dây CD vuông góc với AB và dây DE song song với AB. Tính số đo cung nhỏ BE.....

Bài 16: Cho tam giác ABC lấy M bất kì trên cạnh BC. Từ M kẻ đường song song với AB cắt AC tại D. Từ M kẻ đường thẳng song song với AC cắt AB tại E.....

Bài 17: Cho tam giác ABC vuông tại A. Từ điểm M bất kì trên cạnh BC ( M không trùng với BC ) kẻ đường thẳng song song với AC và AB, chúng cắt AB ở D và AC ở E....

Bài 18: Cho A, B là hai tập hợp tùy ý. Hãy điền kí hiệu tập hợp thích hợp vào chỗ chấm....

Bài 19: Hai xạ thủ độc lập với nhau cùng bắn vào một tấm bia. Mỗi người bắn một viên. Xác suất bắn trúng của xạ thủ thứ nhất là 0,7; của xạ thủ thứ hai là 0,8. Gọi X là số viên đạn bắn trúng bia. Tính kì vọng của X :...

Bài 20: Hai xạ thủ A và B cùng bắn vào bia xác suất để xạ thủ bắn trúng là 0,7 và xác suất để xạ thủ b bán kính là 0,8 tính xác suất để có đúng một xạ thủ bắn trúng bia....

Bài 21: Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?....

Bài 22: Trong hội khỏe Phù Đổng của trường THPT Thanh Miện, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 học sinhkhông tham gia môn nào, 5 học sinhtham gia cả 3 môn. Hỏi số học sinh tham gia chỉ một môn trong ba môn trên là bao nhiêu?...

Bài 23: Cho a,b,c là các số không âm thỏa mãn a + b + c = 1. Chứng minh $b + c \geq 16 a b c$ ....

Bài 24: Cho tam giác ABC nhọn có đường cao AH. Gọi M và N là hình chiếu của H lên AB và AC. CMR: AB . AM = AC . AN...

Bài 25: Tìm hệ số của x⁶ trong khai triển ${(\frac{1}{x} + x^{3})}^{3 n + 1}$ với $x \neq 0,$ biết n là số nguyên dương thỏa mãn điều kiện ${3C}_{n +1}^{2} {+nP}_{2} {=4A}_{n}^{2}$ ....

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.