Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Cho đường tròn tâm O, đường kính AB và một điểm C di động trên đoạn AB

Bài 14: Cho đường tròn tâm O, đường kính AB và một điểm C di động trên đoạn AB. Vẽ các đường tròn tâm I đường kính AC và đường tròn tâm K đường kính BC. Tia Cx vuông góc với AB tại C, cắt (O) tại M. Đoạn thẳng MA cắt đường tròn (I) tại E và đoạn thẳng MB cắt đường tròn (K) tại F

a. Chứng minh tứ giác MECF là hình chữ nhật và EF là tiếp tuyến chung của (I) và (K)

b. Cho AB = 4cm, xác định vị trí điểm C trên AB để diện tích tứ giác IFEK là lớn nhất.

c. Khi C khác O, đường tròn ngoại tiếp hình chữ nhật MECF cắt đường trong (O) tại P (khác M), đường thẳng PM cắt đường thẳng AB tại N. Chứng minh tam giác MPF đồng dạng với tam giác MBN.

d. Chứng minh 3 điểm: N, E, F thẳng hàng

Lời giải:

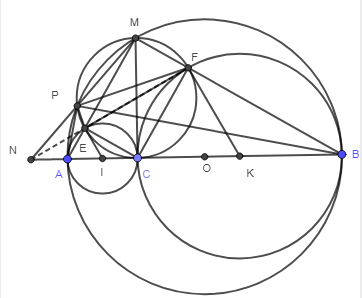
a) Ta thấy MEC và MFC là các tam giác vuông chung cạnh huyền MC nên MECF nội tiếp đường tròn đường kính MC.

Dễ thấy MECF là hình chữ nhật (Tứ giác có 3 góc vuông) nên $\widehat{\text{CEF}}\text{=}\widehat{\text{ECM}}$

Lại có $\widehat{\text{IEC}}\text{=}\widehat{\text{ICE}}\Rightarrow \widehat{\text{IEF}}\text{=}\widehat{\text{MCA}}{\text{=90}}^{\text{o}}$

Hoàn toàn tương tự FE là tiếp tuyến đường tròn (K). Vậy EF là tiếp tuyến chung của hai đường tròn.

b) MECF là hình chữ nhật nên EF = MC.

Do EI và FK cùng vuông góc với EF nên IEFK là hình thang vuông.

$\Rightarrow {\text{S}}_{\text{IEFK}}\text{=}\frac{\left(\text{EI+FK}\right)\text{.EF}}{\text{2}}\text{=}\frac{\left(\text{IC+CK}\right)\text{.MC}}{\text{2}}\text{=}\frac{\text{IK.MC}}{\text{2}}\text{=}\frac{\frac{\text{AB}}{\text{2}}\text{.MC}}{\text{2}}\text{=MC}\le \text{MH}$ với H là điểm chính giữa cung AB.

Vậy để diện tích IEFK lớn nhất thì C nằm chính giữa cung AB. Khi đó 

${\text{S}}_{\text{IEFK}}\text{=2}\left({\text{cm}}^{\text{2}}\right)$

c) Ta thấy $\widehat{\text{MPF}}\text{=}\widehat{\text{MCF}}$  (Hai góc nội tiếp cùng chắn cung MF) $=\widehat{\text{MBN}}$  (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn cung CF)

$\Rightarrow \text{ΔMPF ~ ΔMBN}\left(\text{g - g}\right)$

d) Do $\text{ΔMPF ~ ΔMBN}\Rightarrow \widehat{\text{MFP}}\text{ =}\widehat{\text{ MNB}}$

Mà $\widehat{\text{MFP }}\text{=}\widehat{\text{ MEP}}\Rightarrow \widehat{\text{PNA}}\text{ =}\widehat{\text{ MEP}}$  hay NPEA là tứ giác nội tiếp.

Tương tự PFBN cũng là tứ giác nội tiếp.

Vậy thì ta có: $\widehat{\text{PNE}}\text{ = }\widehat{\text{PAE}}\text{ =}\widehat{\text{ PBM}}\text{ =}\widehat{\text{ PNF}}$

Hay N, E, F thẳng hàng.