Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 105)

Câu 7: a. Giải hệ phương trình:

Phương pháp giải: 

a) Tính x theo y, thay vào phương trình dưới tìm y. Sau đó tìm x.

b) Quy đồng đưa về cùng mẫu và tối giản biểu thức đó.

Lời giải:

a) Ta có: $\{\begin{array}{c}2x+y=5\\ 3x-2y=11\end{array}$​

$\iff \{\begin{array}{c}6x+3y=15\\ 6x-4y=22\end{array}\iff \{\begin{array}{c}7y=-7\\ 2x+y=5\end{array}$​

$\iff \{\begin{array}{c}y=-1\\ 2x=5-y=5-(-1)=6\end{array}\iff \{\begin{array}{c}x=3\\ y=-1\end{array}$​

b) Ta có: $B=({\displaystyle \frac{\sqrt{x}+1}{\sqrt{x}-2}}+{\displaystyle \frac{2\sqrt{x}}{\sqrt{x}+2}}+{\displaystyle \frac{5\sqrt{x}+2}{4-x}}):{\displaystyle \frac{1}{\sqrt{x}+2}}$​

$={\displaystyle \frac{x+3\sqrt{x}+2+2\sqrt{x}(\sqrt{x}-2)-5\sqrt{x}-2}{(\sqrt{x}+2)(\sqrt{x}-2)}}:{\displaystyle \frac{1}{\sqrt{x}+2}}$​

$={\displaystyle \frac{x-2\sqrt{x}+2x-4\sqrt{x}}{(\sqrt{x}+2)(\sqrt{x}-2)}}\cdot {\displaystyle \frac{\sqrt{x}+2}{1}}$​

$={\displaystyle \frac{3x-6\sqrt{x}}{\sqrt{x}-2}}$​​

$=3\sqrt{x}$

Phương pháp chung:

Phương pháp giải hệ phương trình:

Phương pháp 1: Phương pháp thế.

Bước 1: Từ một phương trình của hệ đã cho (coi là phương trình thức nhất), ta biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình thứ hai để được một phương trình mới (chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy để thay thế cho phương trình thức hai trong hệ (phương trình thứ nhất cũng thường được thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia có được ở bước 1).

Bước 3: Giải phương trình một ẩn vừa có, rồi suy ra nghiệm của hệ đã cho.

Bước 4: Kết luận.

Phương pháp 2: Phương cộng đại số.

Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp( nếu cần) sao cho các hệ số của một ẩn nào đó( ẩn x hay y) trong hai phương trình của hệ bằng nhau hoặc đối nhau.

Bước 2: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới

Bước 3: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)

Bước 4: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

Bước 5: Kết luận

Phương pháp 3: Phương đặt ẩn phụ.

Bước 1: Đặt điều kiện của phương trình.

Bước 2: Đặt ẩn phụ, điều kiện của ẩn phụ. Đưa hệ ban đầu về hệ mới.

Bước 3: Giải hệ mới tìm ẩn phụ.

Bước 4: Thay giá trị vào ẩn phụ tìm x và y.

Bước 5: Kết luận.

Phương pháp rút gọn biểu thức:

Bước 1: Vận dụng thích hợp các phép tính và các phép biến đổi đã biết làm xuất hiện căn thức cùng loại;

+ Đưa thừa số A² ra ngoài dấu căn: $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}$ với B ≥ 0;

+ Đưa thừa số vào tròn dấu căn: ;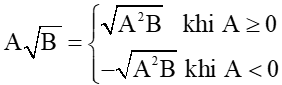

+ Khử căn ở mẫu: $\sqrt{\frac{A}{B}}=\sqrt{\frac{A.B}{B^2}}=\frac{1}{\left|B\right|}\sqrt{A.B}$ với B ≠ 0, AB ≥ 0;

+ Trục căn thức ở mẫu: $\frac{A}{\sqrt{B}}=\frac{A.\sqrt{B}}{B}$; $\frac{m}{\sqrt{A}\pm \sqrt{B}}=\frac{m\left(\sqrt{A}\pm \sqrt{B}\right)}{A-B}$.

Bước 2: Cộng, trừ, các căc thức bậc hai cùng loại.