Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O)

Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O)

Nguyễn Mạnh Tài Ngày: 22-03-2024 Tổng hợp kiến thức

503

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 90)

Đề bài. Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O).

a) Chứng minh AB² = AD.AE.

b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp, chứng minh HB là tia phân giác của $\hat{E H D}$ .

Lời giải:

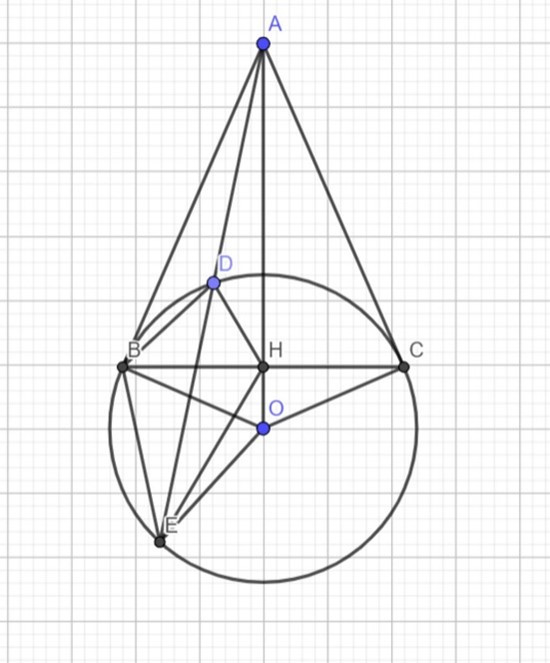
15000 câu hỏi ôn tập môn Toán có đáp án (Phần 100) (ảnh 1)

a) Xét tam giác ABD và tam giác ABE có:

Chung $\hat{A}$

$\hat{A B D} = \hat{A E B}$ (vì AB là tiếp tuyến (O))

⇒ ∆ABD ∽ ∆AEB (g.g)

⇒ $\frac{A B}{A E} = \frac{A D}{A B}$

⇒ AB² = AD.DE

b) Ta có: AB,AC là tiếp tuyến của (O)

⇒AB ⊥ OB, BC ⊥ AO

⇒ BH ⊥ AO

⇒ AB² = AH.AO (Hệ thức lượng trong tam giác vuông)

⇒ AH.AO = AD.AE

⇒ $\frac{A H}{A E} = \frac{A D}{A O}$

Mà $\hat{D A H} = \hat{E A O}$

⇒ ∆ADH ∽ ∆AOE (c.g.c)

⇒ $\hat{A H D} = \hat{A E O}$

⇒ DHOE nội tiếp

⇒ $\hat{A H D} = \hat{D E O} = \hat{E D O} = \hat{E H O}$

⇒ $\hat{D H B} = 90 ° - \hat{A H D} = 90 ° - \hat{E H O} = \hat{B H E}$

Nên: HB là phân giác $\hat{E H D}$ .

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Cho ∆ABC vuông tại A, đường cao AH. Biết 3AB = 2AC. Tính $\sin \hat{A C B}, \tan \hat{A C B}$

Đề bài. Cho tam giác ABC ( AB > BC) có AB + BC = 11cm, $\hat{B} = 60 °$ . Bán kính đường tròn nội tiếp tam giác ABC là $r = \frac{2}{\sqrt{3}}$ cm. Tính đường cao AH của tam giác ABC.

Đề bài. Cho C = 5 + 5² + … + 5²⁰. Chứng minh rằng C chia hết cho 5, 6, 13.

Đề bài. Cho x + y = 12 và xy = 32. Tính x⁴ + y⁴.

Đề bài. Cho dãy số 1, 2, 3, 4, ..., 199, 200; hỏi dãy số có bao nhiêu số chẵn, bao nhiêu số lẻ?

Đề bài. Cho hình vẽ biết : Ax // By, $\hat{x A O} = 32 °, \hat{O B y} = 122 °$ . Chứng tỏ OA vuông góc với OB.

Đề bài. Hình thang ABCD (AB//CD) có AB = 4cm; MN = 6cm với M và N lần lượt là trung điểm của BC và AD. Khi đó độ dài cạnh CD là?

Đề bài. Biết Ax là tia phân giác của $\hat{m A n}$ và $\hat{m A n} = 80 °$ . Tính $\hat{m A x}$ .

Đề bài. Cho $\bar{a b c} + \bar{a c b} = \bar{b c a}$ . Tìm phép cộng đã cho?

Đề bài. Cho các số dương x, y, z thỏa mãn x + 2y + 3z ≥ 20. Tìm GTNN của $A = x + y + z + \frac{3}{x} + \frac{9}{2 y} + \frac{4}{z}$ .

Đề bài. Số nhà của Alice là một số có 4 chữ số chia hết cho 5. Khi cô ấy di chuyển chữ số đầu tiên đến vị trí hàng đơn vị thì nhận thấy rằng số mới có 4 chữ số lớn hơn số nhà của cô ấy là 4707. Hỏi số nhà của Alice là bao nhiêu?

Đề bài. Giải phương trình: (2sinx – 1)(2sin2x + 1) = 3 – 4cos²x.

Đề bài. Một lớp học có 28 nam và 24 nữ. Có bao nhiêu cách chia đều số học sinh vào các tổ với số tổ nhiều hơn sao cho số nam trong các tổ bằng nhau và số nữ trong các tổ bằng nhau? Cách chia nào để mỗi tổ có ít học sinh nhất?

Đề bài. Cho đoạn thẳng AB và hai tia Ax, By vuông góc với AB ở trên cùng một nửa mặt phẳng bờ AB. Gọi O là trung điểm của AB. Xét góc vuông $\hat{m O n}$ quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D. Chứng minh rằng:

Đề bài. Cho các số dương a, b, c thỏa mãn abc = 1.

Đề bài. Nêu khái niệm của khối đa diện? Khối đa diện cần biểu diễn bao nhiêu hình chiếu. Nếu mặt đáy của hình lăng trụ đáy tam giác đều song song với mặt phẳng hình chiếu cạnh thì hình chiếu cạnh là hình gì?

Đề bài. Tìm x biết (x + 2)(x + 2) – (x – 2)(x – 2) = 8x.

Đề bài. Phân tích đa thức thành nhân tử x⁴ – 2x³ + 2x – 1.

Đề bài. Cho $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{a + b + c}$ . Chứng minh $\frac{1}{a^{n}} + \frac{1}{b^{n}} + \frac{1}{c^{n}} = \frac{1}{a^{n} + b^{n} + c^{n}}$ (n là số lẻ).

Đề bài. Tìm số tập con của tập hợp A = {1; 2; 3}.

Đề bài. Gọi S = 1 + 11 + 111 +… + 111….1. Tính S?

Đề bài. Cho tam giác ABC cân tại A. $\hat{A} = 20 °$ . Trên AB lấy điểm D sao cho AD = BC.Tính góc $\hat{B D C}, \hat{A C D}$ .

Đề bài. Cho tập A= (m; m + 2) và tập B = (0; 5). Có bao nhiêu số nguyên m để A giao B khác rỗng?

Đề bài. Cho hình chữ nhật ABCD. Qua C kẻ đường thẳng vuông góc với AC cắt đường thẳng AB, AD theo thứ tự tại E, F. Tia phân giác của góc AFE cắt AC tại H. Gọi K là hình chiếu của A trên FH.

Đề bài. Tìm nghiệm âm lớn nhất của phương trình tan5x.tanx = 1.

Đề bài. Cho hàm số y = ax + 3. Hãy xác định hệ số a trong trường hợp sau:

Đồ thị của hàm số song song với đường thẳng y = -2x.

Đề bài. Cho (O; R) đường kính AB và M nằm trên (O; R) với MA < MB (M khác A và B). Tiếp tuyến tại M của (O; R) cắt tiếp tuyến tại A và B của (O; R) theo thứ tự ở C và D.

Đề bài. Cho y = ax – 3.

a) Đồ thị cắt đường thẳng y = 2x - 1 tại điểm có hoành độ là 2.

Đề bài. Chứng minh sin⁴a + cos⁴a = $\frac{3}{4} + \frac{1}{4} \cos 4 a$ .

Đề bài. Cho tam giác ABC có b = 7; c = 5, $\cos A = \frac{3}{5}$ . Tính đường cao h_a của tam giác ABC?

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH, biết AH : AC = 3: 5 và AB = 15cm.

Đề bài. Cho tam giác đều ABC. Gọi M là điểm thuộc cạnh BC. Gọi E, F lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC. Gọi I là trung điểm của AM, D là trung điểm của BC.

Đề bài. Cho tam giác ABC đều. Trên tia đối của AB lấy điểm D, trên tia đối của BC lấy điểm E, trên tia đối của CA lấy điểm F sao cho AD = BE = CF. Chứng minh rằng tam giác DEF đều.

Đề bài. Tìm x sao cho: (x + 5)(4 − 3x) − (3x + 2)²+ (2x + 1)³= (2x − 1)(4x²+ 2x + 1).

Đề bài. Phân tích số 90 ra thừa số nguyên tố.

Đề bài. Tìm các số tự nhiên n sao cho 6n + 16 chia hết cho n + 2.

Đề bài. Tính cos4a theo cosa.

Đề bài. Tìm $\frac{a}{b}$ thỏa mãn điều kiện $\frac{4}{7} < \frac{a}{b} < \frac{2}{3}$ và 7a + 4b = 1994.

Đề bài. Tìm x, y thỏa mãn 2015(x² + y²) – 2014(2xy + 1) = 25.

Đề bài. Bác Hùng và bác Long cùng làm chung một công việc, sau 2 giờ thì hoàn thành. Nếu bác Hùng làm 1 mình thì sau 5 giờ mới hoàn thành. Hỏi nếu bác Long làm một mình thì sau bao nhiêu lâu sẽ hoàn thành công việc đó?

Đề bài. Lớp 5A có số học sinh nữ bằng $\frac{1}{3}$ số học sinh của lớp. Nếu lớp 5A bớt đi 2 bạn nữ thì số học sinh nữ bằng $\frac{1}{4}$ số học sinh cả lớp. Tìm số học sinh ở lớp 5A.

Đề bài. Tìm x biết 9^{x – 1} = 9.

Đề bài. Cho tam giác ABC. Chứng minh cotA.cotB + cotB.cotC + cotC.cotA = 1.

Đề bài. Tìm 6 chữ số khác nhau a, b, c, d, e, g sao cho $A = \bar{a b c} - \bar{\deg}$ có giá trị nhỏ nhất.

Đề bài. Cho tam giác ABC nhọn, đường cao AH ; Gọi M; N lần lượt là hình chiếu của H trên AB; AC. Chứng minh: MN = AH.sin $\hat{A}$ .

Đề bài. Tìm x biết 18 chia hết cho x và x > 3.

Đề bài. Số nghiệm của phương trình $\sin (x + \frac{π}{4}) = 1$ với π ≤ x ≤ 5π?

Đề bài. Với x > 9. Tìm GTNN của biểu thức $P = \frac{x}{\sqrt{x} - 3}$ .

Đề bài. Một cột đèn có bóng trên mặt đất dài 8,5m . Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ 38°. Tính chiều cao của cột đèn ? (Kết quả làm tròn đến 1 chữ số thập phân).

Đề bài. Cho hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa hai cạnh bên AD và BC. Chứng minh: OA = OB; OC = OD.

Đề bài. Cho cosα = 0,2 với π < a < 2π. Tính $\sin \frac{α}{2}$ .

Đề bài. Cho mảnh vườn hình chữ nhật có độ dài hai cạnh là 6m và 10m. Người ta trồng 4 bồn cỏ có dạng hình tam giác xung quanh như hình vẽ, phần còn lại trồng hoa.

Đề bài. Trong một mảnh vườn hình vuông có kích thước cạnh là 7m (như hình vẽ). Có ba bản vẽ đã được về với yêu cầu phần diện tích đất còn lại (phần màu xám trên bản vê) của vườn là lớn nhất. Bản vẽ nào dùng được? Vì sao?

Đề bài. Một số học sinh dự thi học sinh giỏi toán. Nếu xếp 25 học sinh vào một phòng thì còn thừa 5 học sinh chưa có chỗ. Nếu xếp 28 học sinh vào một phòng thì thừa 1 phòng. Tìm số học sinh dự thi?

Đề bài. Cho tam giác ABC nhọn, vẽ AH vuông góc BC tại H. Chứng minh AC² + BH² = AB² + CH².

Đề bài. Cho 3 đường thẳng (d₁): $y = \frac{1}{2} x - 1$ ; (d₂): y = -2x – 4; (d₃): $y = \frac{1}{2} x - 4$ .

Đề bài. Cho 3 số dương x, y, z có tích bằng 144. Tìm GTNN của biểu thức

Đề bài. Tìm x sao cho 24 chia hết cho x, 30 chia hết cho x, 48 chia hết cho x và x lớn nhất.

Đề bài. Kim giờ và kim phút chỉ thời gian lúc 12 giờ. Người ta để ý rằng cứ cách 1 giờ thì hai kim vuông góc với nhau hai lần. Hỏi thời gian để hai kim vuông góc với nhau lần đầu tiên gần với số nào sau đây?

Đề bài. Cho hai tập hợp A = {1; 2; 3} và B ={1; 2; 3; 4; 5}. Có tất cả bao nhiêu tập X thỏa mãn A ⊂ X ⊂ B?

Đề bài. Tìm giá trị lớn nhất của M = sin⁶x – cos⁶x.

Đề bài. Cho tam giác ABC, D thuộc BC. Qua D kẻ các đường thẳng song song với AC và AB cắt AB, AC lần lượt tại E, F. Chứng minh rằng $\frac{A E}{A B} + \frac{A F}{A C} = 1$ .

Đề bài. So sánh 2³⁰⁰ và 3²⁰⁰.

Đề bài. Cho tam giác ABC, trực tâm H là trung điểm của đường cao AD. Chứng minh rằng: tanB.tanC = 2.

Đề bài. Cho tam giác đều ABC cạnh a, M là trung điểm BC. Tính độ dài $\frac{1}{2} \vec{A B} + 2 \vec{A C}$ .

Đề bài. Tính tổng 1² + 2² + … + n².

Đề bài. Cô giáo chủ nhiệm muốn chia 24 quyển vở, 48 bút bi và 36 gói bánh thành một số phần thưởng như nhau để trao trong dịp sơ kết hợc kì. Hỏi có thể chia được nhiều nhất bao nhiêu phần thưởng? Khi đó mỗi phần thưởng có bao nhiêu quyển vở, bút bi và gói bánh?

Đề bài. Tính: (−0,4)²− (−0,4)³.(−3).

Đề bài. Chứng minh rằng: 11ⁿ⁺² + 12²ⁿ⁺¹ chia hết cho 133.

Đề bài. Cho tập hợp X = {1;2;4;7}.Tập hợp nào là tập hợp con của tập hợp X?

Đề bài. Một sản phẩm được hạ giá 60%. Hỏi sản phẩm đó phải tăng giá lên bao nhiêu % để trở về giá ban đầu?

Đề bài. Góc ngoài của một tam giác cân hơn góc trong kề với nó 90 độ. Tính các góc trong của tam giác đó?

Đề bài. Cho p và p + 2 là các số nguyên tố (p > 3). Chứng minh rằng p + 1 ⋮ 6.

Đề bài. Cho 2 đường thẳng d₁ : y = -4x + m + 1, d₂ : y = $\frac{4}{3}$ x + 15 - 3m.

Đề bài. Phân tích đa thức thành nhân tử: 16x² – (x + 1)².

Đề bài. Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM = 15, BN = 12 và tam giác CMN có diện tích là . Tính độ dài đoạn thẳng MN.

Đề bài. Chọn khẳng định đúng:

Đề bài. Tìm đa thức M, biết: M + (5x² – 2xy) = 6x² + 9xy – y².

Đề bài. Hãy cho biết các tọa độ của điểm M nằm chính giữa một bức tường hình chữ nhật ABCD có cạnh AB = 5m, và cạnh AD = 4m. Lấy trục Ox dọc theo AB, trục Oy dọc theo AD.

Đề bài. Cho hình vẽ, biết a ⊥ c, b ⊥ c và $\hat{A} = 60 °$ . Chứng minh: a // b.

Đề bài. Tính B = – 1 + 7 – 7² + 7³ - … - 7²⁰⁰ + 7²⁰¹ – 7²⁰².

Đề bài. So sánh các số sau: 199²⁰ và 2003¹⁵

Đề bài. So sánh 2 số sau: $\frac{23}{48}$ và $\frac{47}{92}$ .

Đề bài. Cho A = 3 + 3³ + 3⁵ + … + 3²⁰²¹ + 3²⁰²³. Chứng minh A chia hết cho 30.

Đề bài. Chứng minh vì sao số có ước lẻ là số chính phương.

Đề bài. Hai số lẻ có tổng là số nhỏ nhất có 4 chữ số và ở giữa hai số lẻ đó có 4 số lẻ tìm hai số đó.

Đề bài. Chứng minh tam giác ABC có h_a = 2R.sinB.sinC.

Đề bài. Một mảnh vườn hình chữ nhật có chu vi bằng chu vi của một thửa ruộng hình vuông cạnh 80m. Nếu giảm chiều dài mảnh vườn đi 30m và tăng chiều rộng thêm 10m thì mảnh vườn sẽ có hình vuông. Tính diện tích mảnh vườn?

Đề bài. Cho điểm A nằm ngoài đường tròn tâm O, từ A vẽ hai tiếp tuyến AB, AC; B và C là hai tiếp điểm và một cát tuyến ADE đến (O).

Đề bài. Cho $M = \frac{42 - x}{x - 15}$ . Tìm số nguyên x để M đạt GTNN.

Đề bài. Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Điểm M nằm giữa B và C, gọi I là trung điểm của AC, lấy điểm N đối xứng M qua I.

Đề bài. Cho tứ diện ABCD có M nằm trên cạnh AB, N nằm trên cạnh AD thoả MB = 2MA, AN = 2ND. Gọi P là điểm thuộc miền trong của tam giác BCD. Tìm giao tuyến của (MNP) và (ABC).

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.