Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC

Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC

Nguyễn Mạnh Tài Ngày: 10-03-2024 Tổng hợp kiến thức

112

Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 89)

Đề bài. Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC.

a) Xác định giao điểm I, K của AN, MN với (SBD).

b) Tính tỉ số $\frac{I A}{I N}; \frac{K M}{K N}$ .

c) Chứng minh B, I, K thẳng hàng. Tính tỉ số $\frac{I B}{I K}$ .

Lời giải:

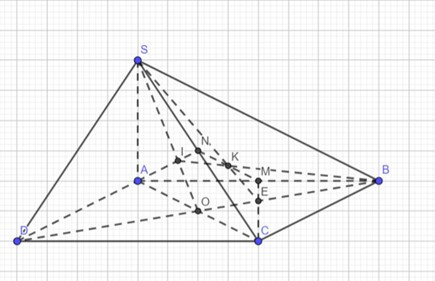
15000 câu hỏi ôn tập môn Toán có đáp án (Phần 99) (ảnh 1)

a) Gọi AC ∩ BD = O, SO ∩ AN = I

⇒ AN ∩ (SBD) = I

CM ∩ BO = E, SE ∩ MN = K ⇒ MN ∩ (SBD) = K

b, c) Ta có M, N là trung điểm AB, SC; O là trung điểm AC, BD

⇒ I, E là trọng tâm SAC, BAC

⇒ $\frac{I A}{I N} = 2$

Ta có: M, K, N thẳng hàng; M ∈ CE, K ∈ SE, N ∈ SC

Suy ra: $\frac{M C}{M E} . \frac{K E}{K S} . \frac{N S}{N C} = 1$

⇒ $3. \frac{K E}{K S} .1 = 1$

⇒ $\frac{K E}{K S} = \frac{1}{3}$

⇒ $\frac{B O}{B E} . \frac{K E}{K S} . \frac{I S}{I O} = \frac{3}{2} . \frac{1}{3} .2 = 1$

Vậy B, I, K thẳng hàng (định lý Menelauyt)

Ta có: S, K, E thẳng hàng nên $\frac{S C}{S N} . \frac{K N}{K M} . \frac{E M}{E C} = 1$

⇒

⇒

Lại có từ S, K, E thẳng hàng nên $\frac{S O}{S I} . \frac{K I}{K B} . \frac{E B}{E O} = 1$

⇒ $\frac{3}{2} . \frac{K I}{K B} .2 = 1$

⇒ $\frac{K I}{K B} = \frac{1}{3}$

⇒ $\frac{K I}{K B + K I} = \frac{1}{3 + 1}$

Hay $\frac{K I}{I B} = \frac{1}{4}$

Suy ra: $\frac{I B}{I K} = 4$ .

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Đề bài. Chứng minh rằng A = 1.5 + 2.6 + 3.7 + … + 2023.2027 chia hết cho 11, 23 và 2023.

Đề bài. Chứng minh rằng $\frac{2}{\sin 4 x} - \tan 2 x = \cot 2 x$ .

Đề bài. Tìm x biết: $x - \sqrt{x - 1} = 3$ .

Đề bài. Cho hình bình hành ABCD. Gọi E và F theo thứ tự là trung điểm của AB và CD

Đề bài. Tìm số tự nhiên n sao cho 2n + 3 chia hết cho n – 2.

Đề bài. Cho $\sin 2 α = \frac{3}{4}$ . Tính giá trị biểu thức A = tanα + cotα.

Đề bài. Cho biết a // b và góc $\hat{A_{1}}$ = 120°.

Đề bài. Cho tam giác ABC cân tại A lấy điểm D bất kì trên AB, lấy điểm E trên tia đối của tia CA sao cho CE = BD. Từ D kẻ đường thẳng song song với AC cắt BC tại F

Đề bài. Chứng minh 3n + 11 và 3n + 2 là hai số nguyên tố cùng nhau với mọi số tự nhiên n.

Đề bài. Cho n thuộc ℕ. Chứng minh rằng n² + n + 1 không chia hết cho 4.

Đề bài. Tính tổng sau: 7²⁰²² – 7²⁰²¹ + 7²⁰²⁰ – 7²⁰¹⁹ + … + 7² – 7.

Đề bài. Tìm số tiếp theo trong dãy:1; 5; 14; 33; 72; ...

Đề bài. Cho hệ phương trình: $\{\begin{cases} x + m y = 2 \\ m x - 2 y = 1 \end{cases}$ . Giải hệ phương trình khi m = 2.

Đề bài. Chứng minh $\frac{\sin^{2} x - \cos^{2} x + \cos^{4} x}{\cos^{2} x - \sin^{2} x + \sin^{4} x} = \tan^{4} x$ .

Đề bài. Cho hình thang cân ABCD (AB // CD) có $\hat{A} = 3 \hat{D}$ . Tính góc A, B, C, D.

Đề bài. Chứng minh rằng với mọi số nguyên n ta có: A = 1⁵ + 2⁵ + … + n⁵chia hết cho B = 1 + 2 + 3 + … + n.

Đề bài. Một đợt bán xe đạp ở cửa hàng sau khi giảm giá lần đầu là 10% và lần thứ hai giảm 5% thì bây giờ lại tăng 8%. Biết giá giảm hay tăng tính dựa theo giá đang bán. Hiện tại giá mỗi chiếc xe đạp là 7387200 đồng. Tính giá gốc ban đầu khi chưa tăng giảm của đợt bán xe đạp này.

Đề bài. Cho tam giác ABC cân tại A có BD và CE là hai đường trung tuyến. Chứng minh:

Đề bài. Tính hợp lý: 5 – (1997 – 2005) + 1997.

Đề bài. Nếu $\tan \frac{β}{2} = 4 \tan \frac{α}{2}$ thì $\tan \frac{β - α}{2}$ bằng bao nhiêu?

Đề bài. Thực hiện phép tính: $\sqrt[3]{45 + 29 \sqrt{2}} + \sqrt[3]{45 - 29 \sqrt{2}}$ .

Đề bài. Cho x, y, z khác 0 và x khác y khác z thỏa mãn x² – xy = y² – yz = z² – zx = a.

Đề bài. Cho hình thang vuông ABCD ( $\hat{A} = \hat{D} = 90 °$ ), có CD = 2AB, gọi H là hình chiếu của D trên AC, M là trung điểm của HC. Chứng minh $\hat{B M D} = 90 °$ .

Đề bài. Người ta đã dùng 400 viên gạch hình vuông có cạnh dài 60 cm để lát nền cho một căn phòng hình vuông (coi các mảnh ghép là không đáng kể). Hỏi nền căn phòng hình vuông đó có cạnh dài bao nhiêu mét?

Đề bài. Giải phương trình: x² – 4x + 4 = 25.

Đề bài. Thực hiện phép tính: $(\frac{1}{4.9} + \frac{1}{9.14} + ... \frac{1}{44.49}) \frac{1 - 3 - 5 - 7 - ... - 49}{89}$ .

Đề bài. Chứng minh rằng với mọi n ∈ ℕ^*, n ≥ 2 ta có: $1 + \frac{1}{2^{2}} + ... + \frac{1}{n^{2}} < 2 - \frac{1}{n}$

Đề bài. Cô giáo muốn chia 240 bút bi, 210 bút chì và 180 tập giấy thành một số phần thưởng như nhau. Hỏi có thể chia được nhiều nhất là bao nhiêu phần thưởng, mỗi phần thưởng có bao nhiêu bút bi, bút chì tập giấy?

Đề bài. Tính tỉ số $\frac{A}{B}$ biết $A = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ... + \frac{1}{2009}$ ; $B = \frac{2008}{1} + \frac{2007}{2} + ... \frac{2}{2007} + \frac{1}{2008}$ .

Đề bài. Cho a là số thập phân có hai chữ số ở phần thập phân. Biết rằng khi làm tròn a đến hàng đơn vị thì được kết quả là 56. Tìm giá trị lớn nhất của a.

Đề bài. Rút gọn biểu thức sau A = sinx.cosx.cos2x.cos4x.cos8x.

Đề bài. Cho cota = 15. Tính giá trị sin2a.

Đề bài. Một khu vườn hình vuông có cạnh bằng 20m, người ta làm một lối đi xung quanh vườn có bể rộng x (m).

Đề bài. Cho hình bình hành ABCD có $\hat{A} = 120 °$ . Tính số đo các góc còn lại của hình bình hành.

Đề bài. Số chính phương khi chia cho 5 thì số dư có thể bằng?

Đề bài. Tìm hai số biết tổng hai số là số lớn nhất có hai chữ số. Hiệu hai số là số lẻ bé nhất có 2 chữ số.

Đề bài. Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.

Đề bài. Tìm hai số có tổng là số bé nhất có 4 chữ số và hiệu là số chẵn lớn nhất có 2 chữ số.

Đề bài. Tổng 2 số là số lớn nhất có 3 chữ số, hiệu của chúng là số lẻ nhỏ nhất có 2 chữ số. Tìm mỗi số.

Đề bài. Cho tam giác ABC có AB = 6, AC = 8, $\hat{A} = 100 °$ . Tính độ dài cạnh BC và bán kính R của đường tròn ngoại tiếp tam giác (làm tròn kết quả đến hàng phần mười).

Đề bài. Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình y = x² và đường thẳng (d) có phương trình y = mx + 3 (với m là tham số).

Đề bài. Cho hai số a, b thỏa mãn a + b = 1.

Tính giá trị của biểu thức P = 2a³ + 6ab + 2b³ – 2024.

Đề bài. Cho tam giác ABC vuông tại A và đường cao AH (H ∈ BC).

Đề bài. Chứng minh rằng m + 2014n chia hết cho 2015 khi và chỉ khi n + 2014m chia hết cho 2015.

Đề bài. Giải phương trình: $\sqrt{x^{2} - 4 x + 3} = 2 \sqrt{25 - 4 x^{2}}$ (*).

Đề bài. Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC). Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.

Đề bài. Xác định các hệ số a, b, c biết: (a – 1)(x² – bx + 3) = 2x² + 5x + c.

Đề bài. Chứng minh rẳng A = 1 + 4 + 4² + 4³ + … + 4²⁰²¹ chia hết cho 21.

Đề bài. Một can xăng đựng 8,5 lít xăng cân nặng 8,22 kg, vỏ can cân nặng 1,25kg. Hỏi một thùng xăng cùng loại có 28,3 lít xăng cân nặng bao nhiêu kg, biết vỏ thùng cân nặng 3,08 kg?

Đề bài. Tìm dư khi chia x⁹⁹ + x⁵⁵+ x¹¹ + x + 7 cho x² + 1.

Đề bài. Tam giác ABC có BC = $\sqrt{5}$ ; AC = 3 và cotC = -2. Tính cạnh AB.

Đề bài. Tìm hệ số a để x⁴ + ax³ + bx – 1 chia hết cho x² – 1.

Đề bài. Tìm x thuộc B(12) và 30 < x < 100.

Đề bài. Cho n điểm phân biệt trên mặt phẳng (n ∈ ℕ, n > 2). Số véctơ khác có cả điểm đầu và điểm cuối là các điểm đã cho bằng.

Đề bài. Cho đoạn thẳng MN = 24cm và điểm O nằm giữa hai điểm M và N. Gọi E là trung điểm của đoạn thẳng OM, F là trung điểm của đoạn thẳng ON, I là trung điểm đoạn thẳng EF. Độ dài đoạn thẳng IE là ...cm.

Đề bài. Giải phương trình cos3x = cos7x.

Đề bài. Cho đoạn thẳng AB và điểm I sao cho $2 \vec{I A} + 3 \vec{I B} = \vec{0}$ .

Đề bài. Cho a, b, c là 3 số dương. Chứng minh: $\sqrt{\frac{a^{3}}{b^{3}}} + \sqrt{\frac{b^{3}}{c^{3}}} + \sqrt{\frac{c^{3}}{a^{3}}} \geq \frac{a}{b} + \frac{b}{c} + \frac{c}{a}$ .

Đề bài. Giải phương trình: $\cos (4 x + \frac{π}{3}) - \sin (x - \frac{π}{4}) = 0$ .

2

Đề bài. Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm AB, SC.

Đề bài. Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(−1;1); B(3;1); C(2;4). Tính chu vi và diện tích tam giác ABC.

Đề bài. Một chữ nhật hình có chiều dài gấp 4 lần chiều rộng. Tăng chiều dài và chiều rộng lên 2m thì diện tích tăng thêm 94m². Tinh chu vi và diện tích ban đầu của hình chữ nhật đó?

Đề bài. Cho tam giác ABC có AB = 2, BC = 3, AC = 4. Tính độ dài đường trung tuyến MA với M là trung điểm của BC.

Đề bài. Cho A = 1 + 2¹ + 2² + 2³ + … + 2²⁰²¹. Tìm x thuộc ℕ sao cho 2^x = A + 1.

Đề bài. Tìm giá trị của m để (m + 1)x² – 2(m + 1)x + 4 ≥ 0 với mọi x thuộc ℝ.

Đề bài. Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC, BC. Điểm I đối xứng với F qua E. Chứng minh tứ giác BDEC là hình thang cân.

Đề bài. Cho tanα = $\frac{1}{2}$ . Tính $\frac{\cos α + \sin α}{\cos α - \sin α}$ .

Đề bài. Cho tam giác ABC có trung tuyến AM , Gọi I là trung điểm AM , D là giao điểm BI và AC. Chứng minh AD = $\frac{1}{3} A C$ .

Đề bài. Tìm điều kiện của tham số m dể phương trình cos²x − 4cosx + m = 0 có nghiệm.

Đề bài. Tính C = $\frac{1}{2} + \frac{1}{2^{3}} + \frac{1}{2^{5}} + ... + \frac{1}{2^{99}}$ .

Đề bài. Cho đường tròn (O) đường kính AB, lấy điểm C thuộc đường tròn (O), với C không trùng A và B. Gọi I là trung điểm của đoạn AC. Vẽ tiếp tuyến của đường tròn (O) tại tiếp điểm C cắt tia OI tại điểm D.

Đề bài. Gọi M là trung điểm của đoạn thẳng AB. Trên 2 nửa phẳng đối nhau bờ AB lần lượt vẽ 2 tia Ax, By vuông góc AB. Trên Ax lấy điểm P, Trên Ay lấy Q sao cho AP = BQ. Chứng minh P, Q, M thẳng hàng.

Đề bài. Cho tam giác ABC, gọi BM và CN lần lượt là các đường trung tuyến sao cho BM vuông góc với CN. Chứng minh cotA = 2 (cotB + cotC).

Đề bài. Chứng tỏ rằng các số có dạng $\bar{a a}$ chia hết cho 11.

Đề bài. Tìm 2 số tự nhiên nhỏ nhất a và b thỏa mãn ƯCLN(a, b) = 12 và a – b = 84.

Đề bài. Cho ba số x, y, z thỏa mãn x² + y² + z² = xy + yz + zx và x + y + z = -3. Tính giá trị biểu thức B = x²⁰²² + y²⁰²³ + z²⁰²⁴.

Đề bài. Viết $\frac{3}{2}$ thành 3 phân số thập phân rồi chuyển 3 phân số đó thành số thập phân.

Đề bài. Cho a, b, c là các số thực dương thỏa mãn a + b + c + ab + bc + ac = 6. Chứng minh rằng: $\frac{a^{3}}{b} + \frac{b^{3}}{c} + \frac{c^{3}}{a} \geq 3$ .

Đề bài. Một can nếu đựng đầy dầu cân nặng 72 kg, nếu đựng nửa số dầu đó thì cân nặng 38kg. Hỏi cái can rỗng thì nặng bao nhiêu ki-lô-gam?

Đề bài. Bác Bình gửi tiết kiệm 500 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức lãi suất kép. Nếu sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi là bao nhiêu?

Đề bài. Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên đường tròn (M khác A; B) vẽ tiếp tuyến với nửa đường tròn, cắt Ax và By lần lượt tại C và D.

Đề bài. Cho tam giác ABC( AB < AC ) có hai đường phân giác CM, BN cắt nhau ở D. Qua A kẻ AE và AF vuông góc với BN và CM. Các đường thẳng AE và AF cắt BC ở I; K.

Đề bài. Cho tam giác ABC có đường cao AH và BD cắt nhau tại I.

Đề bài. Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB và AC.

Đề bài. Rút gọn M = sin(x – y)cosy + cos(x – y)siny

Đề bài. Cho tam giác ABC vuông tại A. Trên tia đối của tia AC kẻ tia Ax. Trên Ax lấy điểm D sao cho AD = AB. Kẻ tia Ay nằm trong BAD. Kẻ DH vuông góc với Ay tại H, kẻ BI vuông góc với Ay tại I.

Đề bài. Cho tam giác ABC vuông tại A, đường cao AH biết BH = 3.6 cm; CH = 6.4 cm

Đề bài. Với mỗi số thực r, ta gọi số nguyên lớn nhất nhỏ hơn hoặc bằng r là phần nguyên của r và kí hiệu là |r|. Có bao nhiêu số nguyên không âm x thỏa mãn $|\frac{x}{2023}| = |\frac{x}{2024}|$ .

Đề bài. Tìm số dư của 2²⁰¹⁷ khi chia cho 11.

Đề bài. Cho khối chóp S.ABCD đáy là hình chữ nhật, cạnh AB = a, AD = 2a. Hình chiếu vuông góc của S xuống ABCD là trung điểm H của AB. Biết SD = 3a. Tính thể tích khối chóp S.ABCD.

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

166

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.