Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 89)

Đề bài. Cho ΔABC cân tại A có AB = 5cm; BC = 6cm. Kẻ phân giác trong AM (M ∈ BC). Gọi O là trung điểm của AC và K là điểm đối xứng của M qua O.

a) Tính diện tích tam giác ABC.

b) Tứ giác ABMO là hình gì? Vì sao?

c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?

Lời giải:

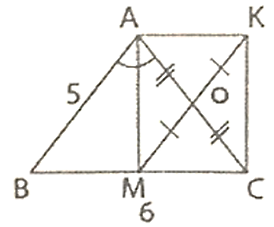
a) Vì M là trung điểm của BC nên:

BM = $\frac{1}{2}BC=\frac{1}{2}.6=3\left(cm\right)$

Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.

Suy ra: AM² = AB² - BM² (Định lí Pytago)

= 52 - 32 = 16(cm)

Suy ra AM = 4cm

S_ABC = $\frac{1}{2}.AM.BC=\frac{1}{2}\mathrm{.4.6}=12\left(c{m}^2\right)$

ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.

Suy ra $\widehat{OAM}=\widehat{OMA}$( ΔAMO cân tại O)

Lại có $\widehat{OAM}=\widehat{MAB}$(AM là tia phân giác góc BAC)

Suy ra $\widehat{OMA}=\widehat{MAB}$

Mà đây là 2 góc ở vị trí so le trong

Suy ra OM // AB

Vậy tứ giác ABMO là hình thang.

c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành .

Lại có $\widehat{AMC}=90°$ (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.

Hình chữ nhật AMCK là hình vuông

⇔ AM = MC = BM

⇔ AM = $\frac{1}{2}BC$

Suy ra tam giác ABC vuông cân tại A.