Cho tam giác MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM

Cho tam giác MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM

Trịnh Thị Phương Huyền Ngày: 07-06-2023 Tổng hợp kiến thức

482

Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 22)

Câu 40: Cho ∆MNP. Gọi D, E, F lần lượt là trung điểm của MN, NP, PM.

a. Chứng minh tứ giác MDEF là hình bình hành.

b. ∆MNP có điều kiện gì thì tứ giác MDEF là hình chữ nhật.

Lời giải:

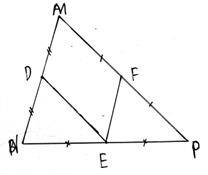
Tài liệu VietJack

a. Xét ∆MNP có: D là trung điểm MN; E là trung điểm NP (gt)

⇒ DE là đường trung bình của ∆MNP ⇒ DE // MP

Chứng minh tượng tự: EF // MN

Xét tứ giác MDEF có: MD // EF (do EF // MN); DE // MF (do DE // MP)

⇒ MDEF là hình bình hành

b. Để hình bình hành MDEF là hình chữ nhật $\Leftrightarrow \hat{F M D} = 90 °; \hat{P M N} = 90 °$

Vậy tứ giác MDEF là hình chữ nhật ⟺ ∆MNP có $\hat{N M P} = 90 °$ .

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Câu 1: Giải phương trình: cos3x.cosx = cos2x....

Câu 2: Tính ${(a - b - c)}^{3}$ ....

Câu 3: Giải hệ phương trình: $\{\begin{matrix} x^{4} + 2 x^{3} y + x^{2} y^{2} = 2 x + 9 \\ x^{2} + 2 x y = 6 x + 6 \end{matrix}$ ....

Câu 4: Hình vuông có cạnh bằng 2 thì đường chéo hình vuông đó bằng bao nhiêu?..

Câu 5: Chứng minh $A \cup B = A \cap B$ thì A = B....

Câu 6: Xác định các tập hợp A $\cup B$ và $A \cap B$ với: A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím}.....

Câu 7: Cho $Δ A B C$ đều cạnh a. Tính độ dài vectơ $\vec{A B} - \vec{A C}$ và $\vec{A B} + \vec{A C}$ ......

Câu 8: Cho phương trình: $\cos (2 x - \frac{π}{3}) - m = 2$ . Tìm m để phương trình có nghiệm....

Câu 9: Giải phương trình sinxcosx + 2(sinx + cosx) = 2....

Câu 10: Một cánh đồng lúa thực nghiệm hình chữ nhật có chiều dài 1200m, chiều rộng bằng $\frac{3}{5}$ chiều dài. Người ta cấy giống lúa với năng xuất đạt 5 tấn trên 1 ha. Hỏi cả cánh đồng lúa thực nghiệm đó sẽ thu hoạch được bao nhiêu tấn thóc?...

Câu 11: Phân tích đa thức sau thành nhân tử: x² – 6x – 7....

Câu 12: Chứng minh phương trình sau có nghiệm: $x^{3} - 2 x - 1 = 0$ ....

Câu 13: Cho ∆ABC có CB = 2, CA = 3 và $\hat{A C B} = 90 °$ . Tính độ dài cạnh AB....

Câu 14: Tìm GTLN của hàm số y = 6sin2x – 8cos2x – 2....

Câu 15: Giải phương trình sau: $\cos^{2} 2 x = \frac{1}{4}$ ....

Câu 16: Giải phương trình: cos2x – 3cosx + 2 = 0...

Câu 17: Giải phương trình: $\cos^{2} x + 3 \cos x + 2 = 0$ ....

Câu 18: Giải phương trình: cos4x + cos2x + 1 = 0...

Câu 19: Giải phương trình: 1 + cos4x = cos2x....

Câu 20: Giải phương trình tanx = cotx...

Câu 21: Giải phương trình: $2 \sin^{2} x + \sin x \cos x - \cos^{2} x = 0$ ...

Câu 22: Cho một số có ba chữ số biết rằng khi viết thêm chữ số 5 vào bên phải số đó thì số đó tăng thêm 2444 đơn vị. Tìm số đó.....

Câu 23: Giải phương trình: $x^{2} - y^{2} + 2 x - 4 y - 10 = 0$ với x, y nguyên dương....

Câu 24: Tia đối của tia NM là ?....

Câu 25: Giải phương trình: $2 x^{2} - 2 x - 3 = 0$ ....

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6 Lữ Ngọc My My

55

Toán Tổng hợp kiến thức

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1 Lữ Ngọc My My

52

Toán Tổng hợp kiến thức

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84 Lữ Ngọc My My

42

Toán Tổng hợp kiến thức

Tìm x; y nguyên 2xy + 2x - y = 8

Tìm x; y nguyên 2xy + 2x - y = 8 Lữ Ngọc My My

43

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.