Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 21)
Câu 18: Cho tam giác OAB vuông tại A, OA = 3 cm, AB = 4 cm, đường cao AH (H thuộc OB)
a) Tính AH.
b) Vẽ đường tròn (O; OA) cắt tia AH tại C. Chứng minh: CB là tiếp tuyến của đường tròn (O; OA).
Lời giải:
a)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH ta có:
(cm)
b)
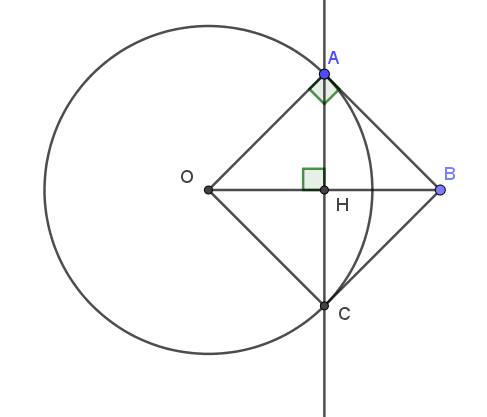
Xét đường tròn O có: OH là một phần đường kính, AC là dây cung, OH vuông góc với AC tại H nên H là trung điểm của AC
Do đó, OB là đường trung trực của AC nên ta có: AB = CB
Xét tam giác OAB và tam giác OCB có:
AB = CB
OB chung
OA = OB (cùng bằng bán kính)
Do đó, tam giác OAB bằng tam giác OCB
Do đó, ta có:
Vậy BC vuông góc với bán kính OC nên BC là tiếp tuyến của đường tròn tâm O
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 2: Cho đồ thị (d): y = (3m − 2)x + m − 2 với m là tham số..
Câu 4: Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:...
Câu 5: Gieo một con xúc xắc cân đối đồng chất 2 lần, tính xác suất để biến cố có tích 2 lần số chấm khi gieo xúc xắc là một số chẵn....
Câu 6: Giải bất phương trình sau: 3x2 – 4x + 4 > 0....
Câu 7: Giải bất phương trình sau: – 3x2 + x + 4 ≥ 0....
Câu 8: Cho hàm số y = f(x) = ax2....
Câu 9: Cho hàm số y = f(x) = ax2 – 2...
Câu 10: Tìm x, biết: x + 456,95 × 8 = 5248....
Câu 11: Phân tích đa thức thành nhân tử: 2x2 – 3x – 2...
Câu 12: Giải phương trình: ....
Câu 14: Một vật hình hộp chữ nhật có kích thước (30×20×10 cm)...
Câu 16: Với giá trị nào của a và b thì đa thức x3 + ax2 + 2x + b chia hết cho đa thức x2 + x + 1....
Câu 17: Tìm x để có nghĩa ?...
Câu 18: Cho tam giác OAB vuông tại A, OA = 3 cm, AB = 4 cm, đường cao AH (H thuộc OB)...
Câu 19: Giải phương trình với ẩn số nguyên dương n thỏa mãn:....
Câu 20: Có bao nhiêu cách xếp 5 nam và 5 nữ thành hàng dọc sao cho 5 nam đứng liền nhau ?...
Câu 21: Có bao nhiêu số tự nhiên lớn hơn 4000 có 4 chữ số được lập từ các số 1, 2, 5, 7 nếu:..
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
