Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 17)
Câu 37: Cho tam giác OPQ cân tại O có I là trung điểm của PQ. Kẻ IM // OQ.
(M ∈ OP), IN // OP (N ∈ OQ). Chứng minh rằng:
1) Tam giác IMN cân tại I.
2) OI là đường trung trực của MN.
Lời giải:
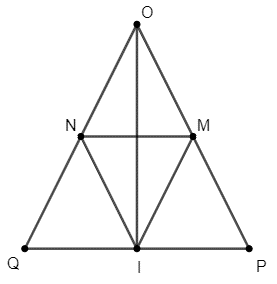
1) Xét ∆OPQ có I là trung điểm của PQ và IN // OP.
Do đó N là trung điểm của OQ (*).
Xét ∆OPQ có I là trung điểm của PQ, IM // OQ.
Do đó M là trung điểm của OP (**).
Từ (*) và (**) suy ra MN là đường trung bình của OPQ suy ra MP = NQ.
Xét ∆MPI và ∆NQI có
MP = NQ (cmt)
(gt)
PI = QI (gt)
Do đó ∆MPI = ∆NQI
Suy ra: IM = IN hay ∆IMN cân tại I.
2) Ta có: OM = ON nên O nằm trên đường trung trực của MN (1)
Ta có: IM = IN nên suy I nằm trên đường trung trực của MN (2)
Từ (1) và (2) suy ra OI là đường trung trực của MN.
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 2: Phân tích đa thức thành nhân tử: x4 + x2 + 1...
Câu 3: Liệt kê tất cả các ước của các số sau: 530; 240; 438...
Câu 4: Phân tích đa thức thành nhân tử: 12x2 + 5x – 12y2 + 12y – 10xy – 3...
Câu 5: Cho trước hai điểm phân biệt A, B. Tìm tập hợp các điểm M thỏa mãn...
Câu 6: Cho hai điểm B; C phân biệt. Tập hợp những điểm M thỏa mãn là:..
Câu 8: Mẹ có một số kẹo. Nếu mẹ chia số kẹo thành 6 phần bằng nhau thì dư 3 cái....
Câu 12: Giải phương trình tan3x = tanx...
Câu 14: Cho tam giác ABC có . Chọn câu đúng:...
Câu 18: Tìm x, biết: cos2x – 3sinx.cosx – 2sin2x – 1 = 0....
Câu 20: Cho hàm số y = f(x) = 3x4 – 4x2 + 3. Trong các mệnh đề sau, mệnh đề đúng?...
Câu 21: Tìm x, biết: 8x3 – 12x2 + 6x – 1 = 0....
Câu 22: Cho a + b + c + d = 0. Với a, b, c, d > 0. Chứng minh rằng:..
Câu 25: Giải phương trình: sin2x – 5sinx.cosx + 6cos2x − 1 = 0.....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
