Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:
Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 7)
Câu 35: Cho tam giác ABC có hb + hc = 2ha. Chứng minh rằng:
Lời giải:
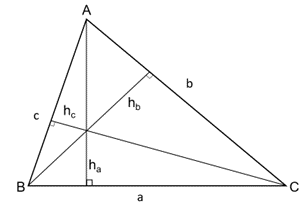
Ta có: hb + hc = 2ha
Áp dụng định lý Sin trong tam giác ABC:
; (R: bán kính đường tròn ngoại tiếp tam giác)
.
Vậy .
Định lí sin trong tam giác
Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
= 2R,
trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:
Câu 1: Tính tổng 3 + 6 + 12 + 24 + … + 3072...
Câu 3: Giữa các số 7 và 35 hãy đặt thêm 6 số nữa để được một cấp số cộng...
Câu 4: Cho 4 điểm A, B, C, D. Chứng minh: ....
Câu 8: Giải phương trình sau: 5sin x – 2 = 3(1 – sin x)tan2 x....
Câu 9: Chứng minh rằng x8n + x4n + 1 chia hết cho x2n + xn + 1, với mọi số tự nhiên n....
Câu 15: Cho hình bình hành ABCD. Dựng ....
Câu 16: Cho tam giác ABC nhọn. Vẽ AH vuông góc với BC tại H. Chứng minh rằng:...
Câu 23: Tìm m để đa thức A(x) = x3 – 3x2 + 5x + m chia hết cho đa thức B(x) = x – 2....
Câu 25: Cho ba điểm A(– 4; 0), B(0; 3) và C(2; 1). Xác định tọa độ của vectơ .....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
