Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau

Bài 30: Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?

Lời giải: Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:

+ Chia khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành hai khối lăng trụ tam giác bằng nhau: ABC.A'B'C' và  BCD.B'C'D'

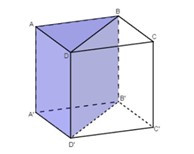
+ Tiếp theo, lần lượt chia khối lăng trụ $ABD.A^{\text{'}}{B}^{\text{'}}{D}^{\text{'}}$ và $BCD.B^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ thành ba tứ diện: $DAB{B}^{\text{'}};DA{A}^{\text{'}}B$ và  $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}.$

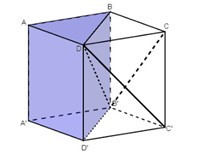
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:

Hai khối tứ diện DABB' và DAA'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB')         (1)

Hai khối tứ diện DAA'B' và DD'A'B' bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B'A'D)         (2)

Từ (1) và (2) suy ra ba khối tứ diện $DAB{B}^{\text{'}},DA{A}^{\text{'}}{B}^{\text{'}}$ và $D{D}^{\text{'}}{A}^{\text{'}}{B}^{\text{'}}$ bằng nhau.

Tương tự, ba khối tứ diện $DCB{B}^{\text{'}},DC{C}^{\text{'}}{B}^{\text{'}},D{D}^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}$ cũng bằng nhau.

Vậy khối lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ được chia thành sáu khối tứ diện bằng nhau.

Phương pháp giải

Để chia một khối lập phương thành 6 tứ diện bằng nhau, ta có thể làm như sau:

Bước 1: Xác định các đỉnh và các mặt của khối lập phương

• Khối lập phương có 8 đỉnh và 6 mặt.
• Mỗi mặt của khối lập phương là một hình vuông.

Bước 2: Vẽ các đường chéo trong khối lập phương

Vẽ các đường chéo từ các đỉnh của khối lập phương, mỗi đường chéo chia mặt của khối lập phương thành 2 tam giác.

Bước 3: Xác định các tứ diện

Mỗi tứ diện được tạo thành bởi 4 đỉnh, trong đó 3 đỉnh cùng nằm trên một mặt hình vuông và 1 đỉnh là trung điểm của một cạnh của khối lập phương.

Bước 4: Kiểm tra đảm bảo tứ diện bằng nhau

Đảm bảo rằng diện tích và hình dạng của 6 tứ diện thu được là như nhau bằng cách tính toán và so sánh các độ dài cạnh, diện tích mặt của từng tứ diện.

Kết luận

Quá trình chia khối lập phương thành 6 tứ diện bằng nhau yêu cầu tính toán kỹ lưỡng và vẽ hình học chính xác để đảm bảo các tứ diện thu được có diện tích như nhau.