Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 câu hỏi thường gặp môn Toán có đáp án (phần 109)

Câu 6: Cho tam giác ABC vuông ở A, D thuộc cạnh BC. Gọi I,K lần lượt là hình chiếu của D trên AB và AC. Gọi AH là đường cao của tam giác ABC. Chứng minh góc IHK bằng 90 độ

Phương pháp giải: 

Nhận xét hình học:

Tứ giác $AIDK$ là hình chữ nhật vì các góc $\angle AID$ và $\angle AKD$ đều bằng $90^\circ$.

Tâm $O$ của hình chữ nhật $AIDK$ là trung điểm của cả $AD$ và $IK$.

Xét tam giác $\triangle AHD$:

$AH$ là đường cao, $O$ là trung điểm của $AD$.

Chứng minh $OH = OI = OK$, tức $O$ là tâm đường tròn ngoại tiếp tam giác $HIK$.

Kết luận góc vuông:

Dựa vào tính chất đường kính trong đường tròn ngoại tiếp, $\triangle HIK$ vuông tại $H$.

Lời giải:

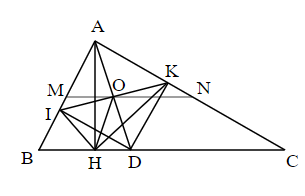
a) 2 đoạn AD và IK cắt nhau ở O. Nối O với H.

Xét tứ giác AIDK: $\widehat{IAK}=\widehat{AID}=\widehat{AKD}={90}^o$ => Tứ giác AIDK là hình chữ nhật

O là tâm của hình chữ nhật AIDK => O là trung điểm AD & IK; OA=OD=OI=OK

Xét $\mathrm{\Delta }$AHD: $\widehat{AHD}=90°$; O là trung điểm AD => OH=OA=OD

=> OH=OI=OK. Trong $\mathrm{\Delta }$HIK có: O là trung điểm IK; OH=OI=OK

=> $\mathrm{\Delta }$HIK vuông tại H => $\widehat{IHK} = 90°$ (đpcm).