Tailieumoi.vn biên soạn và giới thiệu các dạng bài tập môn Toán gồm các kiến thức lý thuyết và thực hành, các dạng bài tập thường gặp giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 67)

Câu 32: Cho nửa đường tròn tâm O đường kính AB =2R và điểm M nằm trên đường tròn đó (M ≠ A, B) tiếp tuyến tại điểm M của nửa đường tròn tâm O cắt các tiếp tuyến tại A và B. Lần lượt tại các điểm C, D. Gọi E là giao điểm của OC với AM, gọi F là giao điểm của OD và BM.

a) Chứng minh CD = AC + BD.

b) Chứng minh EF vuông góc BD và EF là tiếp tuyến đường tròn đi qua các điểm M, D, F.

Lời giải:

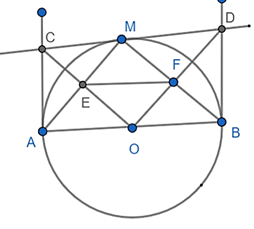
a) Vì CA, CM là tiếp tuyến của (O) nên AC = CM

Tương tự: DM = DB

Suy ra: CM + DM = AC + BD ⇒ CD = AC + BD

b) Vì CA, CM là tiếp tuyến của (O) nên OC ⊥ AM tại E là trung điểm AM

Tương tự: OF ⊥ BM tại F là trung điểm BM

Suy ra: EF là đường trung bình của ∆MAB

⇒ EF // AB mà AB ⊥ BD nên EF ⊥ BD

Vì MB ⊥ OD tại F nên G là trung điểm DM, là tâm đường tròn ngoại tiếp ∆MDF

Mà GF là đường trung bình ∆MBD

Suy ra: GF // BD ⇒ GF ⊥ EF

Vậy EF là tiếp tuyến của đường tròn đi qua M, D, F.