Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 16)

Câu 24: Cho hàm số: $y=\frac{m}{3}{x}^3-(m-1)x^2+3(m-2)x+1$ để hàm số đạt cực đại x₁, x₂ thỏa mãn x₁ + 2x₂ = 1 thì giá trị của m bằng?

Lời giải:

Ta có: y' = mx² – 2(m – 1)x + 3(m – 2) (m ≠ 0)

Để hàm số có cực đại tại x₁ và cực tiểu tại x₂ thì phương tình

y' = mx² – 2(m – 1)x + 3(m – 2)  = 0 có 2 nghiệm phân biệt.

 = (m – 1)² – 3m(m – 2) = −2m² + 4m + 1 > 0

$\Rightarrow 1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$ (1)

Khi đó áp dụng định lý Vi−ét, ta có:

$\left\{\begin{array}{l}{x}_1+x_2=\frac{2(m-1)}{m}\left(2\right)\\ x_1{x}_2=\frac{3(m-2)}{m}\left(3\right)\end{array}\right.$

Mặt khác theo bài cho ta có: x₁ + 2x₂ = 1 (4)

Nếu 2x₁ + x₂ = 0 (5)

Từ (4) và (5) $\Rightarrow x_1=-\frac{1}{3};x_2=\frac{2}{3}$ .

Thay vào (2) ta có: $2\frac{m-1}{m}=\frac{1}{3}\Rightarrow m=\frac{6}{5}$

Thay vào (3) ta có: $3\frac{m-2}{m}=-\frac{2}{9}\Rightarrow m=\frac{54}{9}$

Suy ra 2x₁ + x₂ ≠ 0

Khi đó nhân hai vế của (4) với 2x₁ + x₂ ta có:

(x₁ + 2x₂)(2x₁ + x₂) = 2x₁ + x₂

 2(x₁ + x₂)² + x₁x₂ = 2x₁ + x₂

Thay (2) và (3) vào ta được:

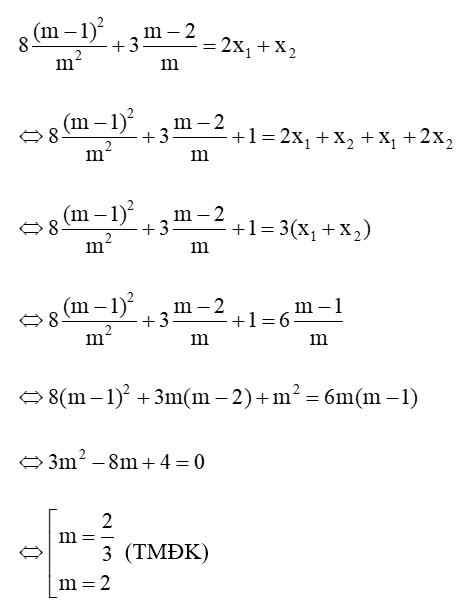
Vậy có hai giá trị m thỏa mãn yêu cầu bài toán là: $m=\frac{2}{3}$ ; m = 2.