Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b^2 + c^2 = 5a^2

Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b^2 + c^2 = 5a^2

Trịnh Thị Thu Hiền Ngày: 20-05-2023 Tổng hợp kiến thức

2.9 K

Tailieumoi.vn biên soạn và giới thiệu bộ câu hỏi Toán gồm các kiến thức lý thuyết và thực hành, giúp học sinh ôn tập và bổ sung kiến thức cũng như hoàn thành tốt các bài kiểm tra môn Toán. Mời các bạn đón xem:

Top 1000 Bài tập thường gặp môn Toán có đáp án (Phần 11)

Câu 11: Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b2 + c2 = 5a2.

Lời giải:

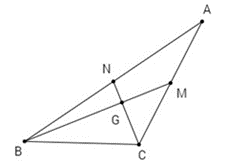
Tài liệu VietJack

Gọi G là giao điểm của hai trung tuyến BM, CN.

Áp dụng công thức tính trung tuyến, ta có:

• $G B^{2} = \frac{4}{9} B M^{2} = \frac{1}{9} (2 a^{2} + 2 c^{2} - b^{2})$ ;

• $G C^{2} = \frac{4}{9} C N^{2} = \frac{1}{9} (2 a^{2} + 2 b^{2} - c^{2})$ .

BM và CN vuông góc với nhau khi BG2 + CG2 = BC2.

$\Leftrightarrow \frac{1}{9} (2 a^{2} + 2 c^{2} - b^{2}) + \frac{1}{9} (2 a^{2} + 2 b^{2} - c^{2}) = a^{2}$

$\Rightarrow$ 4a2 + b2 + c2 = 9a2

$\Rightarrow$ b² + c² = 5a².

Xem thêm các bài tập thường gặp môn Toán hay, chọn lọc khác:

Câu 1: Tìm x để (x + 17) chia hết cho (x + 3)....

Câu 2: Tìm tập hợp X sao cho {a; b} ⊂ X ⊂ {a; b; c; d}....

Câu 3: Tìm tập hợp X sao cho X ⊂ A và X ⊂ B, trong đó....

Câu 4: Một bạn học sinh dùng các khối lập phương xếp thành một cái tháp. Em tính giúp bạn xem để xếp được tháp cao 8 tầng thì cần chuẩn bị bao nhiêu khối lập phương.....

Câu 5: Cho hai tập hợp E = (2; 5] và F = [2m − 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5....

Câu 6: Cho hai tập hợp A = (2; 5] và B = [2m − 3; 2m + 3]. Tìm m để A giao B là một tập có độ dài bằng 5....

Câu 7: Chứng minh: $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{3} + \sqrt{4}} + ... + \frac{1}{\sqrt{79} + \sqrt{80}} > 4$ ....

Câu 8: Chứng minh rằng: $\frac{R}{r} = \frac{\sin A + \sin B + \sin C}{2 \sin A \sin B \sin C}$ ....

Câu 9: Chứng minh S = 2R².sin A.sin B.sin C với S là diện tích tam giác ABC....

Câu 10: Cho tam giác ABC, đường cao AH. Biết $A B = 4 c m, A C = 4 \sqrt{2} c m, B C = 4 \sqrt{3} c m .$ Chứng minh tam giác ABC vuông. Tính độ dài các đoạn thẳng AH, HB.....

Câu 11: Cho tam giác ABC. Chứng minh điều kiện cần và đủ để hai trung tuyến BM và CN vuông góc với nhau là b2 + c2 = 5a2....

Câu 12: Cho tam giác ABC. Chứng minh c.m_c = b.m_b khi b² + c² = 2a²....

Câu 13: Giải phương trình: $\cos (3 x + \frac{π}{3}) - \cos (x - \frac{π}{6}) = 0$ ...

Câu 14: Giải phương trình: $\sin (x + \frac{π}{3}) - \cos (3 x + \frac{π}{6}) = 0$ ....

Câu 15: Một cái thang dài 4 m đang dựa vào tường, chân thang cách chân tường 2 m. Tính góc tạo bởi thang với mặt đất và với mặt tường....

Câu 16: Một cái thang dài 4 m, đặt dựa vào một bức tường, góc giữa thang và mặt đất là 60°. Hỏi khoảng cách giữa chân thang và tường bằng bao nhiêu?....

Câu 17: Trong mặt phẳng Oxy cho điểm M(2; 3). Trong bốn điểm sau, ảnh của M qua phép đối xứng qua đường thẳng x − y = 0 là...

Câu 18: Trong mặt phẳng tọa độ Oxy, cho điểm M (−2; 3). Hỏi trong bốn điểm sau, điểm nào là ảnh của M qua phép đối xứng với trục là đường thẳng d: x − y = 0?...

Câu 19: Tính giá trị biểu thức A = 3x³y + 6x²y² + 3xy³ tại $x = \frac{1}{2}; y = - \frac{1}{3}$ ....

Câu 20: Rút gọn biểu thức A = 1 + 2 + 2¹ + 2² + … + 2²⁵....

Câu 21: Tìm giá trị nhỏ nhất của A = x² − 6x + 17....

Câu 22: Tìm giá trị nhỏ nhất hoặc lớn nhất của biểu thức sau: ...

Câu 23: Tìm giá trị lớn nhất nhỏ nhất của hàm số: $y = 3 + 2 \cos (x + \frac{π}{3})$ ...

Câu 24: Hàm số $y = - 2 co s (x - \frac{π}{3}) - 5$ đạt giá trị lớn nhất tại giá trị bao nhiêu?...

Câu 25: Cho các số nguyên tố p, q thỏa mãn p² − 2q² = 17. Tính p + q...

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.